统计学方法

zscore
原理：
Z-score 基于正态分布理论，它量化了数据点距离数据集平均值的相对标准偏差。
通常，如果 Z-score 的绝对值超过某个阈值（如3或更大），该数据点就被认为是异常值。这是因为正态分布下，大约99.7%的数据点应当落在平均值 ± 3标准差的范围内。

import numpy as np

def find_outliers_1d(data, z_threshold=3):
    """
    使用Z-score方法在一维数据中查找异常值。
    
    参数:
    data (np.ndarray): 一维数据数组
    z_threshold (float): Z-score阈值，默认为3
    
    返回:
    np.ndarray: 异常值数组
    """
    
    # 计算数据的均值和标准差
    mean = np.mean(data)
    std_dev = np.std(data)

    # 计算Z-score并找到绝对值大于阈值的索引
    z_scores = np.abs((data - mean) / std_dev)
    outlier_indices = np.where(z_scores > z_threshold)[0]

    # 返回异常值
    return data[outlier_indices]

分位数IQR
IQR 方法不依赖于数据的正态分布特性，而是基于数据的四分位数进行异常值检测。它关注的是数据内在的局部变异度，尤其适合处理非正态分布的数据。

计算过程包括：

计算数据的第一四分位数（Q1）、第三四分位数（Q3）和四分位距（IQR）：IQR=Q3−Q1IQR = Q3 - Q1IQR=Q3−Q1。
设定异常值的界限：

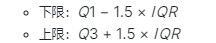
任何低于下限或高于上限的数据点被认为是异常值。

# 假设有如下数据
data = pd.Series([10, 20, 30, 40, 50, 60, 70, 800, 900, 1000])

# 计算四分位数
q1 = data.quantile(0.25)
q3 = data.quantile(0.75)
iqr = q3 - q1

# 计算异常值边界
lower_bound = q1 - 1.5 * iqr
upper_bound = q3 + 1.5 * iqr

# 标记和筛选异常值
outliers = data[(data < lower_bound) | (data > upper_bound)]
normal_values = data[(data >= lower_bound) & (data <= upper_bound)]

print("异常值：", outliers)
print("正常值：", normal_values)

这两种方法各有优势：Z-score 对于接近正态分布的数据效果良好，而 IQR 更能应对偏斜分布和其他复杂分布类型的数据，且不受极值影响较小。

机器学习

DBSCAN

想到用聚类做，k均值聚类会受到异常值影响，用密度聚类DBSCAN试一下

DBSCAN原理
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)，是一种基于密度的空间聚类算法。其主要原理是通过探测数据集中的点的密度分布来识别和划分集群。DBSCAN的基本思想是：

核心点（Core Points）: 如果一个点在其ε邻域（以该点为中心，半径为ε的领域）内的样本点数量大于或等于一个预设的阈值MinPts，则称该点为核心点。

边界点（Border Points）: 边界点是指那些邻域内的点数少于MinPts，但是位于某个核心点的ε邻域内的点。

噪声点（Noise Points）: 其他既不是核心点也不是边界点的点被标记为噪声点。

聚类过程：从一个核心点开始，遍历其邻域内的所有点，不断递归地扩张集群，直到没有新的点可以加入为止。最终，所有连接的核心点及其可达边界点构成一个簇。

from sklearn.neighbors import NearestNeighbors
from sklearn.cluster import DBSCAN,KMeans
from sklearn.preprocessing import StandardScaler

from sklearn.cluster import DBSCAN
import numpy as np

data = np.array([167, 163, 167, 168, 140, 167, 167, 168, 167, 88, 88, 88, 90, 91, 92, 91, 91, 91, 92, 92]).reshape(-1, 1)

# 创建并拟合模型
dbscan = DBSCAN(eps=5, min_samples=2).fit(data) # 与周围点距离5以内的点不超过1个，算异常值

# 获取每个样本的簇标签
labels = dbscan.labels_

# 打印簇标签
print(labels)

LF (isolation forest)

原理： Isolation Forest（孤立森林）是一种无监督的异常检测算法，它基于随机森林的思想，通过构造决策树的方式分离数据点。不同于传统的分类或回归任务中使用的决策树，孤立森林的目标是尽可能快地将数据点“隔离”或“孤立”。正常点往往处在数据集的密集区域，被孤立所需要穿越的决策树层数较少；算法通过统计所有树上数据点被孤立所需要的平均路径长度来衡量其异常程度。

原则：

随机性：在构建孤立森林时，每一次划分特征和划分点的选择都是随机的。
反直觉性：异常点由于分布在数据集的边缘或者孤立区域，通过随机划分更容易被孤立，因此其在决策树上的路径长度相对较短。
异常度量：每个数据点的异常得分可通过其在所有iTree中的平均路径长度获得，得分越低表示越有可能是异常点。

实践：在Isolation Forest 中，即使是相同的数值，由于其在不同子集或在不同特征空间中的相对位置不同，导致其被孤立的速度也会有所差异，进而影响其异常得分。所以，同一个数值在不同的数据分布或模型训练过程中，可能被识别为异常，也可能不被视为异常。效果太差。

def find_outlier_by_LF(data):
    '''
    同一个值 有些是异常 有些不是异常
    :param data:
    :return:
    '''
    # 假设X是一维或二维数据集
    X = data.reshape(-1, 1)

    # 初始化孤立森林模型
    iso_forest = IsolationForest(contamination='auto', random_state=42)

    # 训练模型
    iso_forest.fit(X)

    # 计算异常得分
    scores = iso_forest.decision_function(X)
    outliers_indices =  np.where(scores <  -0.3)[0]
    outlier_value = data[np.where(outliers_indices)]
    # 判断异常点
    # y_pred = iso_forest.predict(X)

    # 负值表示异常点，正值表示正常点
    # outliers = np.where(y_pred == -1)[0]

    # 输出异常值
    print("异常值索引：", outliers_indices)

LOF

Local Outlier Factor (LOF) 是一种基于密度的异常检测算法，由Breunig等人在2000年提出。LOF算法通过计算数据点的局部密度，并将其与同区域内的其他点进行对比，来评估一个数据点是否为异常值。

基本原理：

局部密度：LOF首先计算每个数据点的局部密度，即该点周围的邻居点的密度。局部密度通过k近邻（k-NN）算法来估计，一般通过计算某点的k近邻的距离来反映其密度。

LOF值：LOF值是通过比较一个数据点自身的局部密度与它周围k个最近邻点的局部密度的平均值来得出的。如果一个数据点的局部密度明显低于其邻居点的局部密度，则其LOF值会很高，这意味着它可能是一个异常值。
判别异常：通常，一个点的LOF值越大，它作为异常值的可能性就越高。一个阈值可以用来区分正常点和异常点。

LOF算法主要包括以下几个步骤：

• 计算每个点的k近邻集合。
  -计算每个点的可达距离（Reachability Distance），这是该点到其k近邻中某个点的距离除以那个点的半径（该点的k近邻中最远点的距离）。
  -计算每个点的局部密度，也就是它的k近邻的平均可达距离。
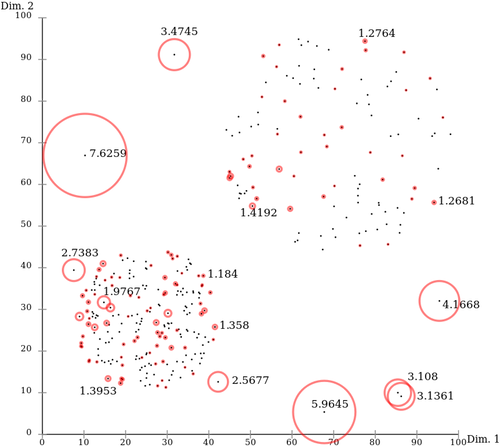
  -计算LOF值，即每个点的局部密度除以其k近邻的平均局部密度。(如果数据点 p 的 LOF 得分在1附近，表明数据点p的局部密度跟它的邻居们差不多;如果数据点 p 的 LOF 得分小于1，表明数据点p处在一个相对密集的区域，不像是一个异常点；如果数据点 p 的 LOF 得分远大于1，表明数据点p跟其他点比较疏远，很有可能是一个异常点。)
  根据设定的LOF阈值，确定异常值。

原则

• 密度一致性：正常点的局部密度与其邻居的局部密度相似，而异常点的局部密度明显偏低。
• 局部性质：仅依赖于数据点的局部邻域信息，无需预先知道数据的全局分布。
  参考：
  https://zhuanlan.zhihu.com/p/28178476
  

def find_outlier_by_LOF(data,percentile = 1):
    '''

    :param data: 一维数据
    :param percentile: percentile = 1假设异常数据1%，保留前99%的数据作为正常数据
    :return:
    '''

    # 假设X是你的二维数据集
    X = data.reshape(-1, 1) # 替换为你的二维数据

    # 初始化LOF模型，这里设定邻居数量为20
    lof = LocalOutlierFactor(n_neighbors=5, contamination="auto")

    # 计算LOF分数
    lof.fit(X)

    # # 获取离群分数
    scores = -lof.negative_outlier_factor_
    #
    # # 获取异常值索引
    # outlier_indices = np.where(scores < 2)[0]
    #
    # # 输出异常值
    # outliers = X[outlier_indices]


    threshold = np.percentile(scores, percentile)
    outlier_indices = np.where(scores <= threshold)[0]
    outlier_value = data[np.where(outlier_indices)]
    return outlier_value

PCA

本质： PCA异常检测的本质是利用主成分分析（PCA）降维的特性来识别数据中的异常值。PCA通过最大化数据的方差来提取最重要的特征（主成分），从而将高维数据转化为低维空间表示。正常数据通常在PCA降维后的低维空间中有较强的集聚性，而异常值由于其独特的属性，会在降维后的空间中表现为远离正常数据点的形态。

降维原理：PCA通过线性变换将原始数据投射到一组新的坐标系中，新坐标系的基向量（主成分）是按照方差从大到小排列的。

异常检测原理：正常数据在PCA降维后主要集中在占据大部分方差的前几条主成分上，而异常值由于其在某些维度上的偏离较大，所以在低维空间中的投影可能落在远离正常数据分布的区域，或者在次要主成分上的投影值较大，表现为较大的残差。

PCA异常检测的第一原则：

保留关键信息原则：首先保留那些解释数据方差最多的主成分，确保大部分正常数据的信息得以保留。
残差最大化原则：异常值在主成分分析后的残差空间中具有相对较大的投影，即异常值在PCA降维后未能被主要主成分解释的那部分变异要大于正常值。

fromsklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
import numpy as np
def find_outlier_by_PAC(data):
    # 假设X是一维或二维数据集
    X = data.reshape(-1, 1)

    # 数据预处理
    scaler = StandardScaler()
    X_scaled = scaler.fit_transform(X)

    # 执行PCA降维，这里保留95%的方差
    pca = PCA(n_components=0.95)
    X_pca = pca.fit_transform(X_scaled)

    # 计算残差或重构误差（此处以残差为例）
    residuals = np.linalg.norm(X_scaled - pca.inverse_transform(X_pca), axis=1)

    # 设定阈值，这里可以采用统计方法如四分位数或固定阈值
    threshold = 0.1 #np.percentile(residuals, 95)

    # 标记异常值
    outliers = np.where(residuals > threshold)[0]

    # 输出异常值
    print("异常值索引：", outliers)