前言
因为论文学习的需要,入门了一下李群和李代数,觉得B站的这个视频讲得不错:视频地址为机器人学——李群、李代数快速入门,这里记录一下。
- 前言
- 引入:一些常见的例子
- 为什么用到李群
- 李群理论的基本内容
- 群的定义
- 李群的定义
- 群的运算
- 李群的拓扑
- 切空间和李代数
- 指数映射
- S O ( 2 ) SO(2) SO(2)的指数映射
- 大写的指数映射
- 加号和减号运算符
- 伴随矩阵
- 李群的微积分
- 李群的雅克比
- 李群的微分规则
- 李群上的扰动
- 李群上的合并
- 李群的应用
- EKF(卡尔曼滤波)
- 图像SLAM
- 更多资料和工具
引入:一些常见的例子
S 1 S^1 S1:单位复数
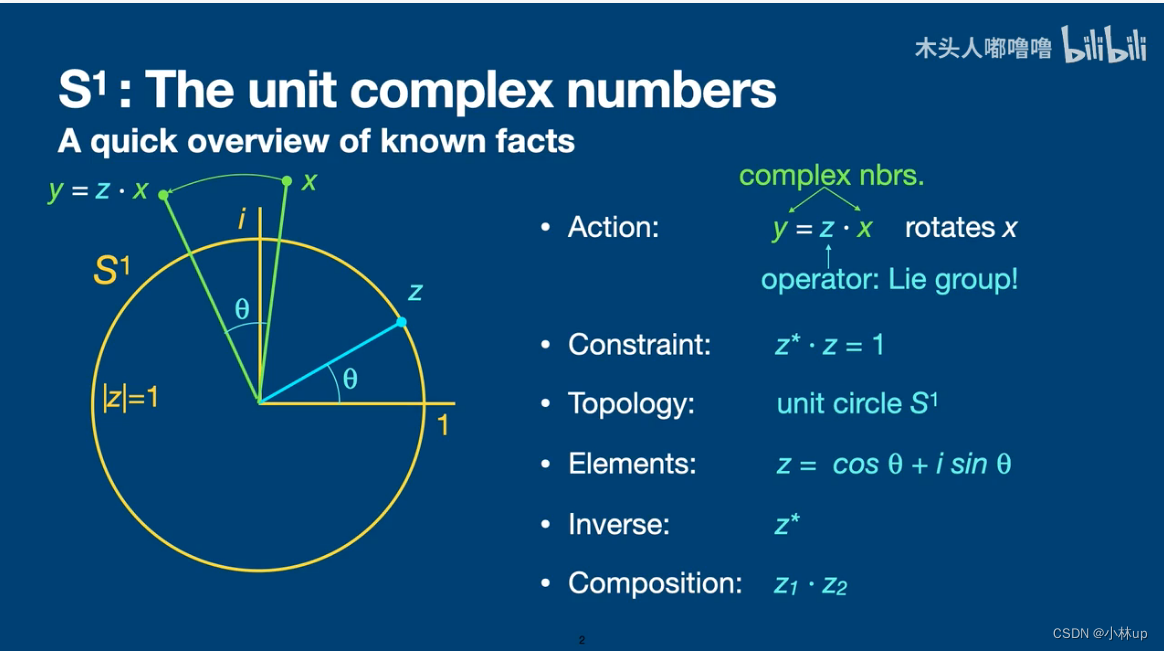
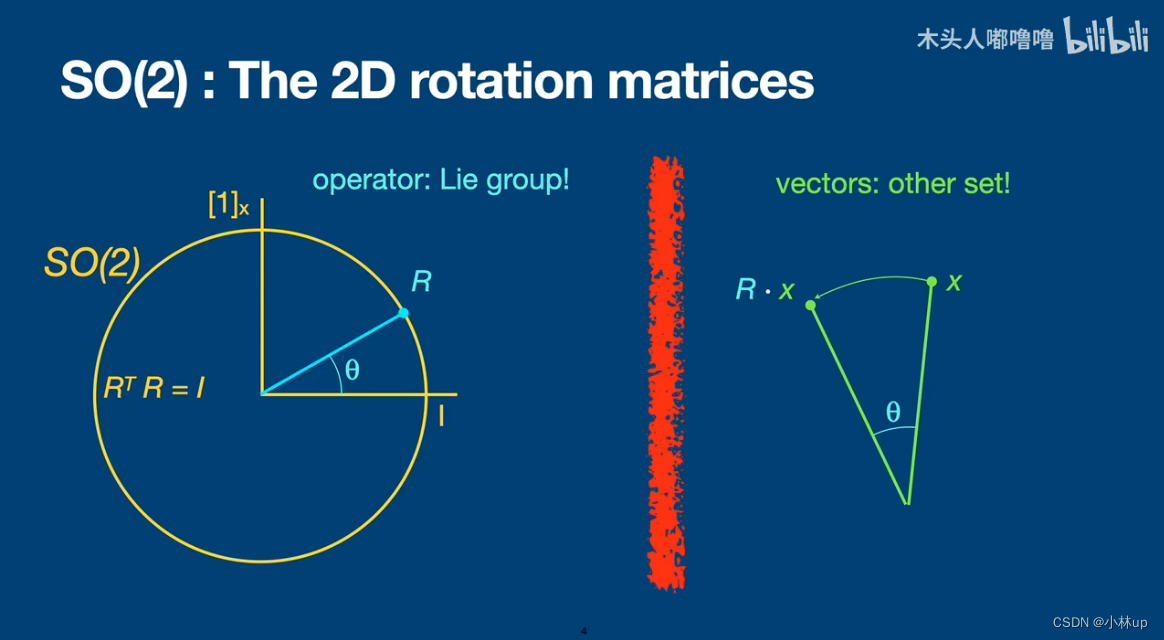
S O ( 2 ) SO(2) SO(2):二维旋转矩阵
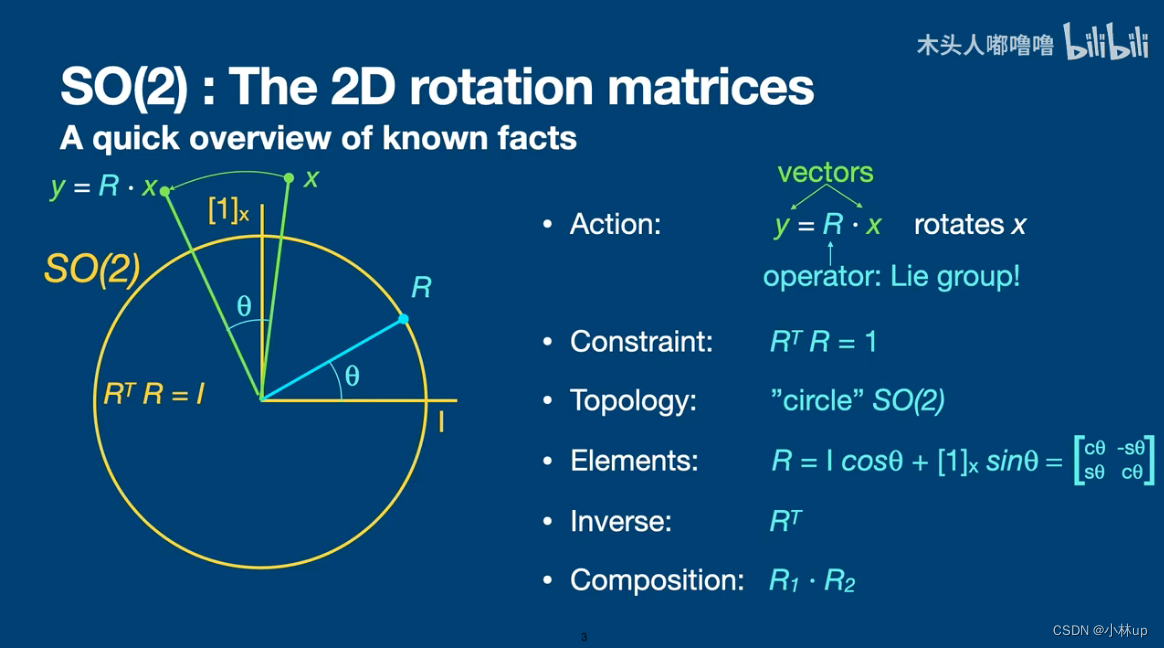
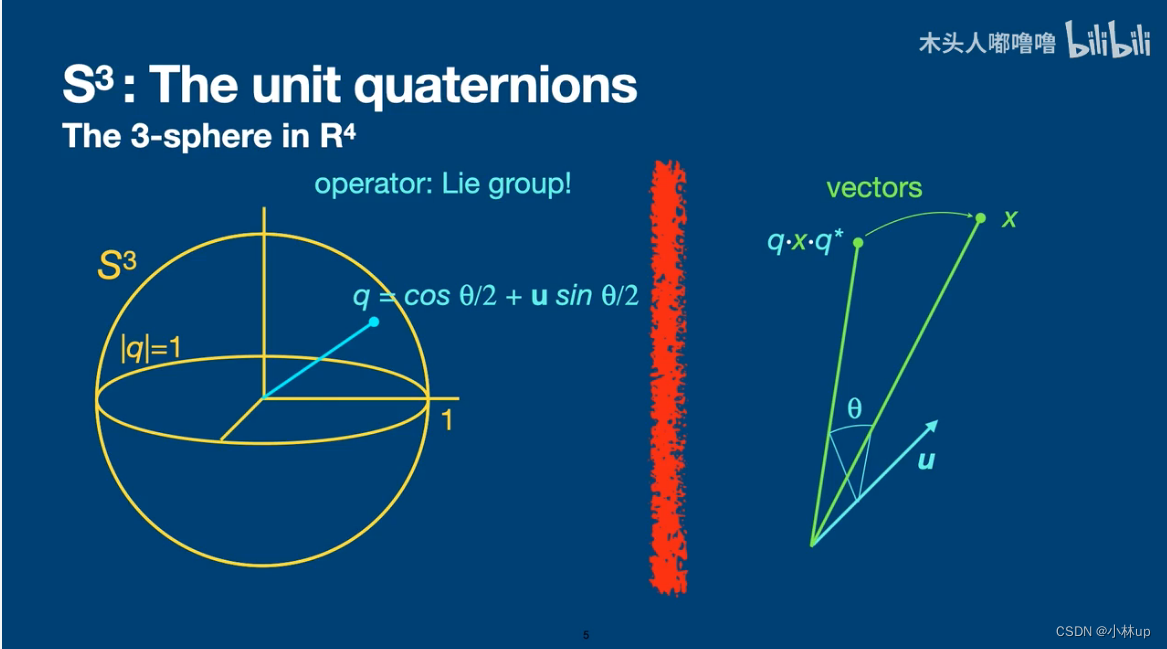
S 3 S^3 S3:单位四元数
为什么用到李群
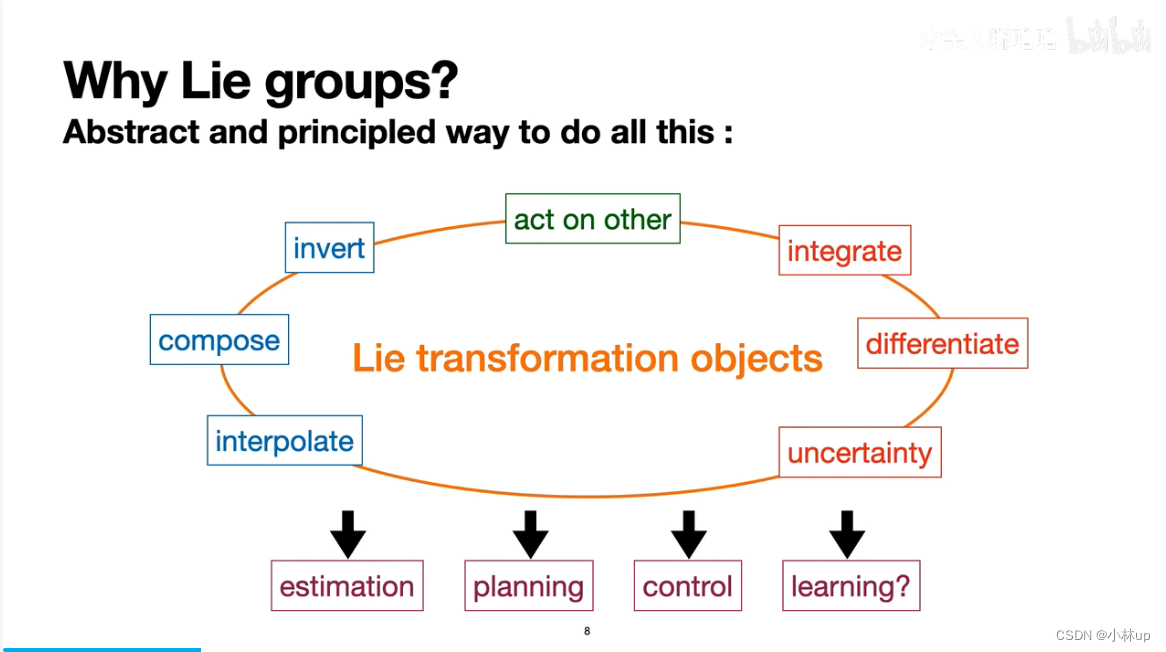
李群理论的基本内容

群的定义

李群的定义
李群不仅是群还是光滑的流形。
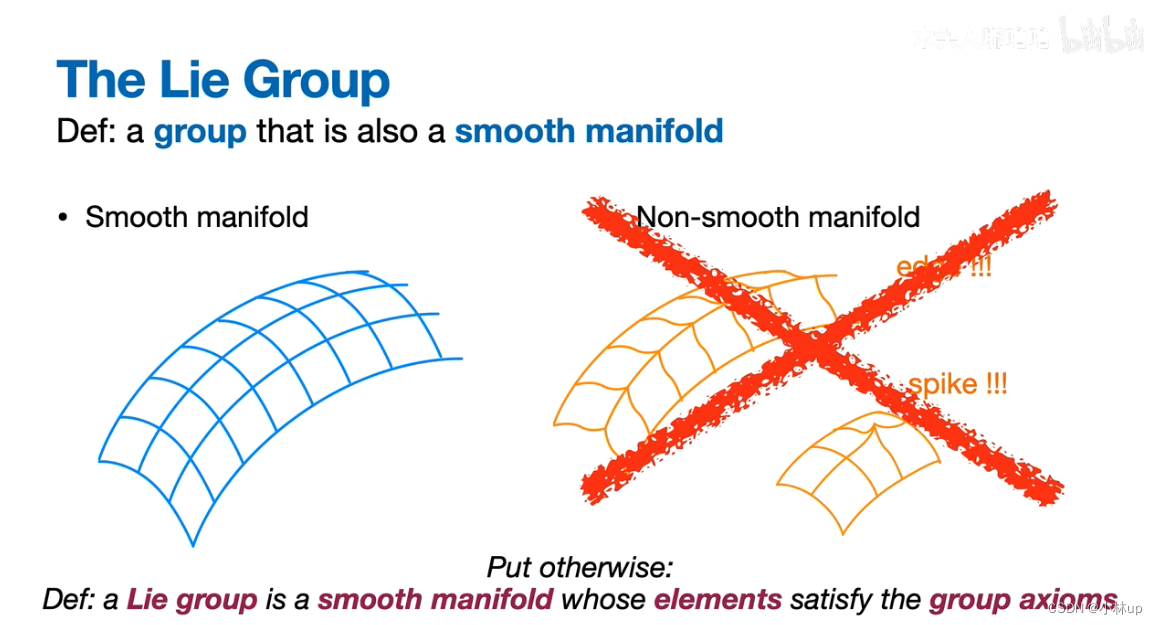
群的运算

李群的拓扑
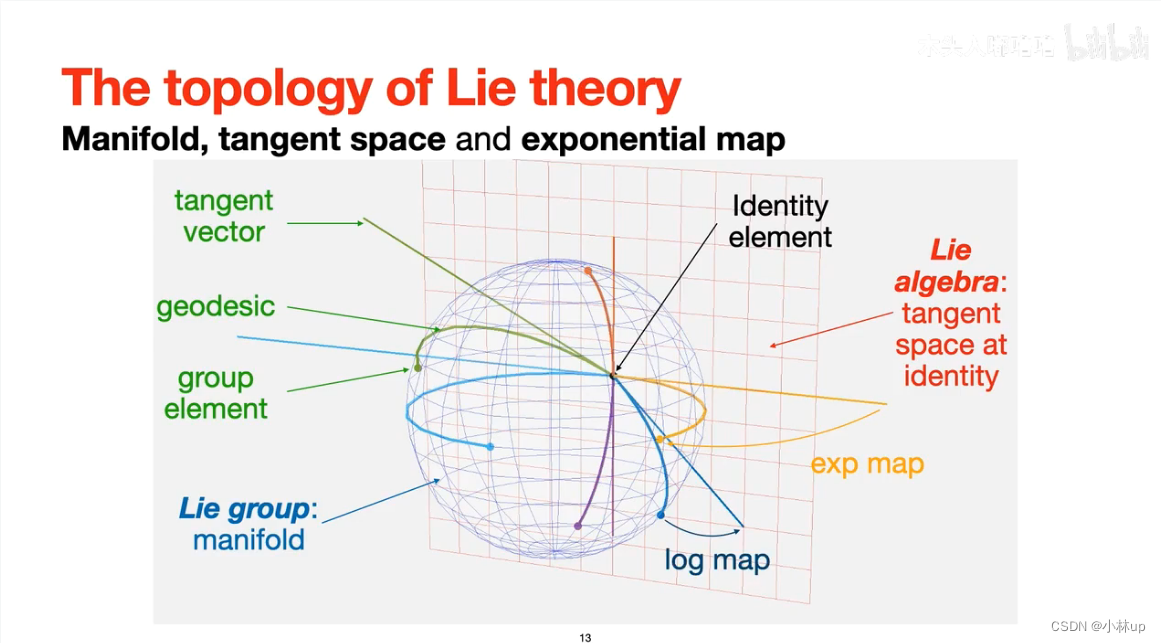
切空间和李代数
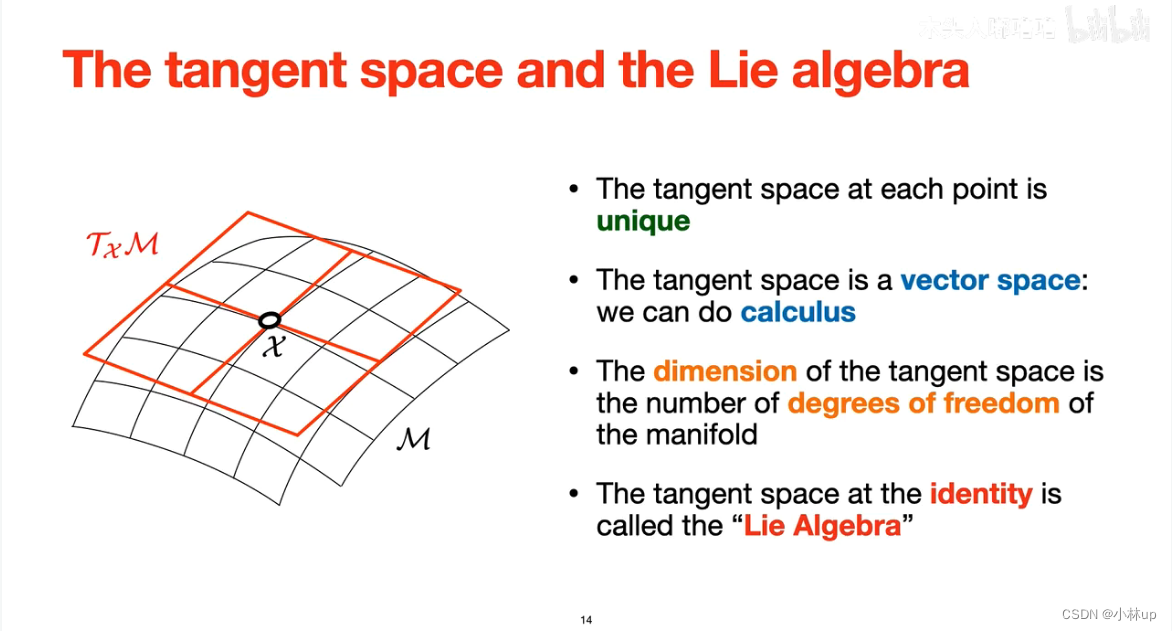
李代数是李群流形上单位元的切空间。李群流形的自由度(维数)和其切空间维数相等。
S 1 S^1 S1的切空间
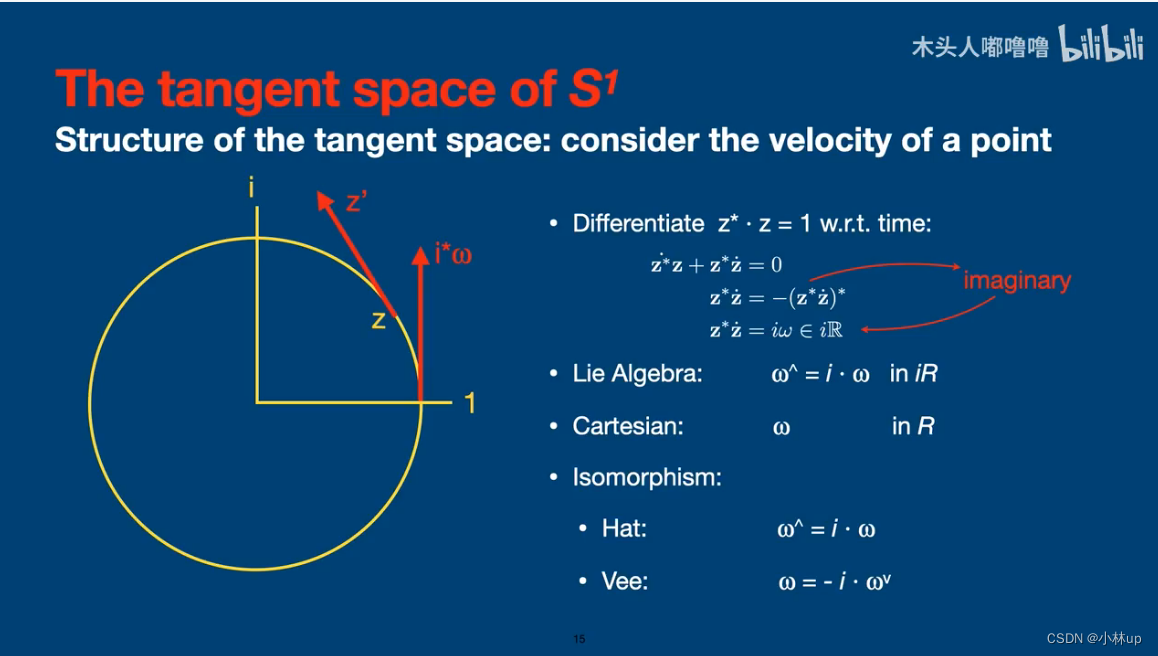
S O ( 3 ) SO(3) SO(3)的切空间
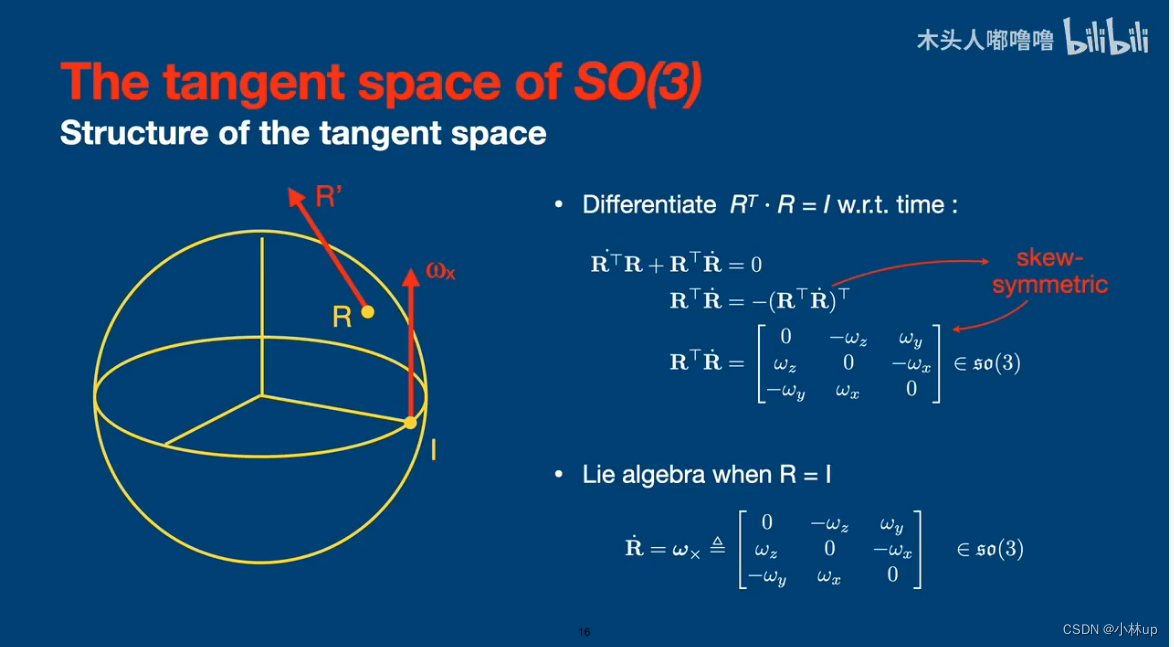

指数映射
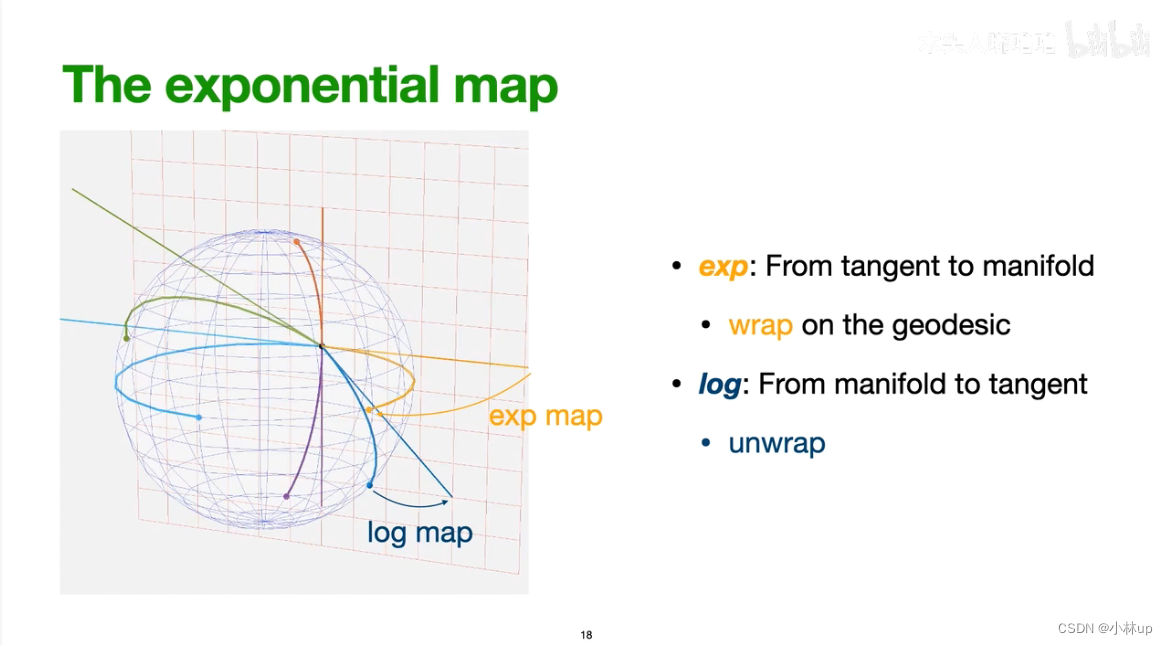
指数映射 e x p exp exp是从切空间到流形,对数映射 l o g log log是从流形到切空间。
S O ( 2 ) SO(2) SO(2)的指数映射
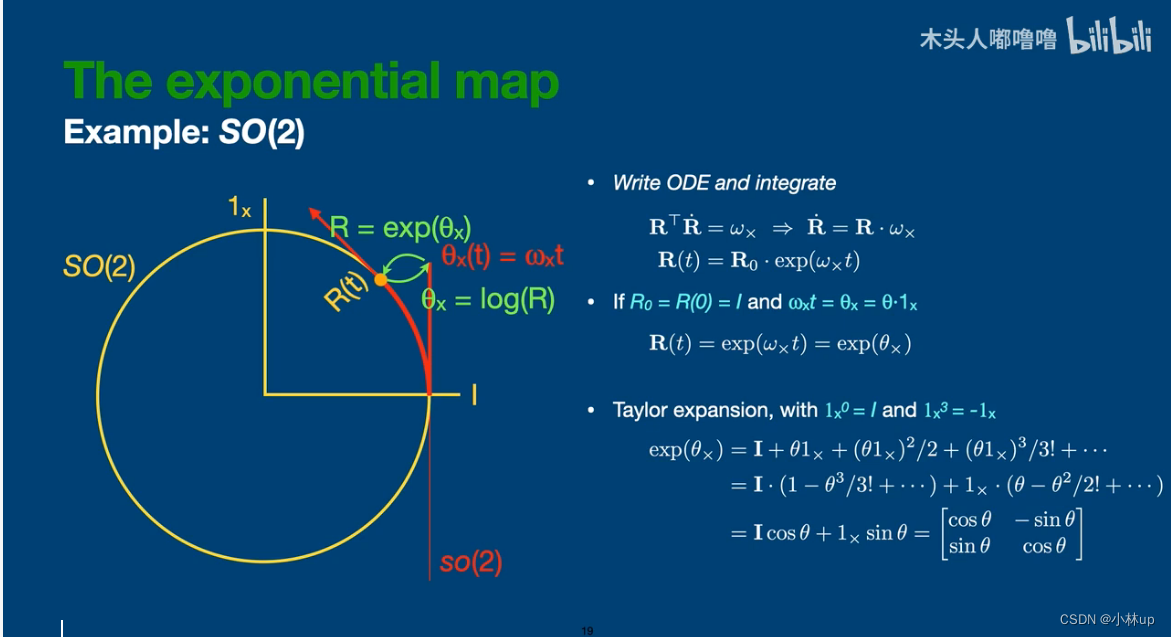
大写的指数映射
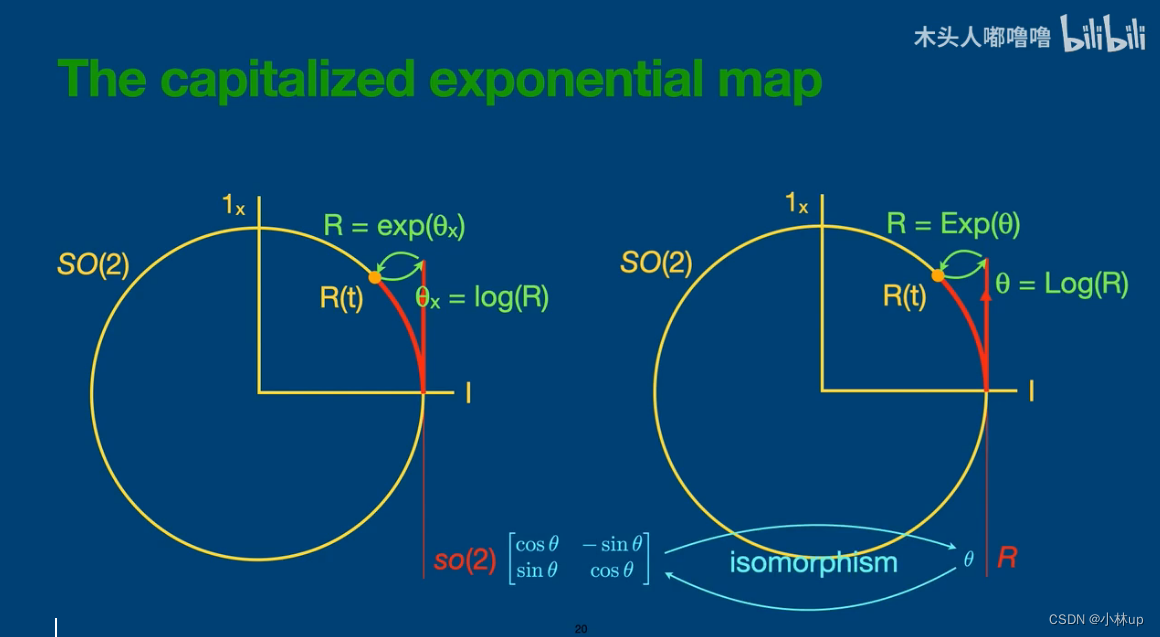

加号和减号运算符
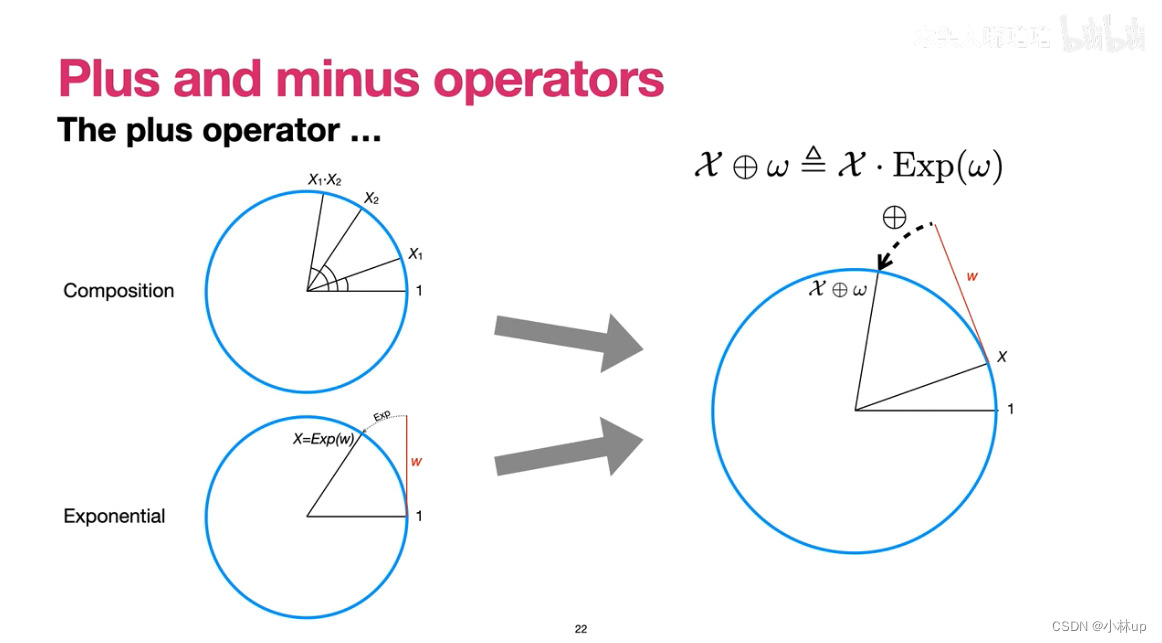

伴随矩阵
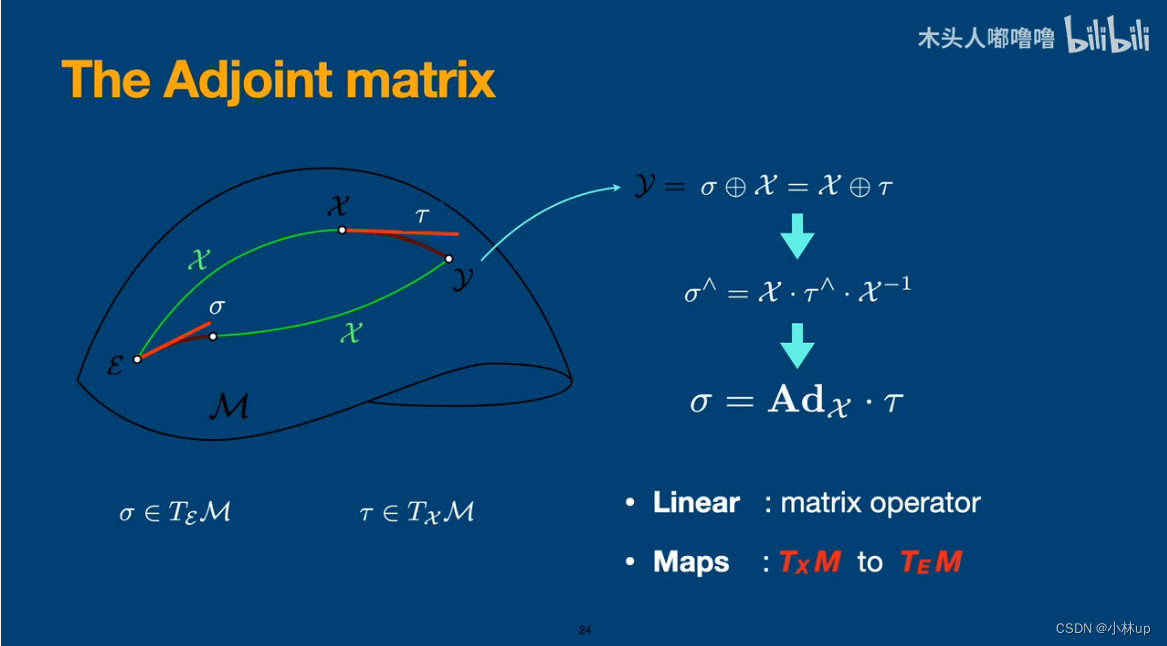
李群的微积分
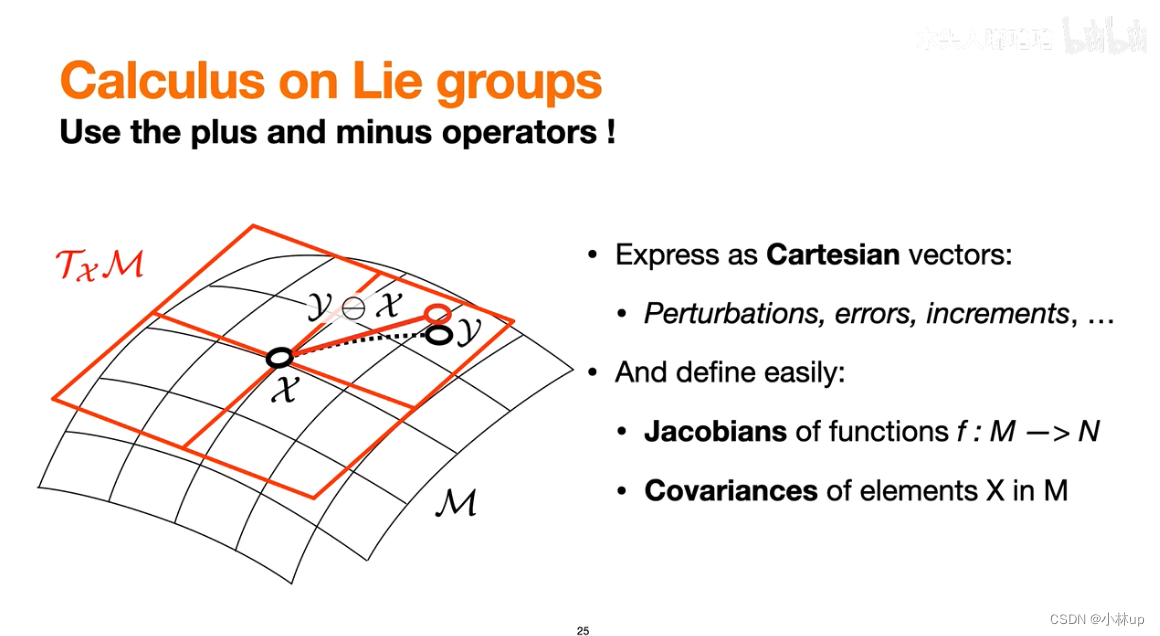
李群的雅克比

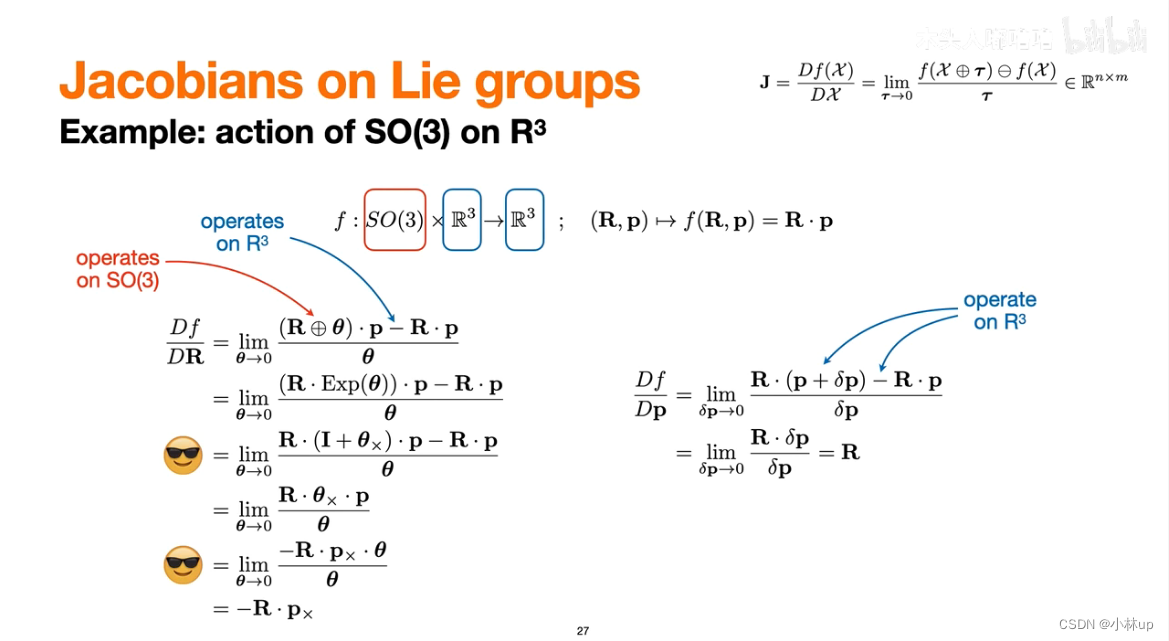

李群的微分规则

李群上的扰动

李群上的合并
(我也不知道integration翻译成合并是否妥当,有更好的可以指出)

李群的应用
EKF(卡尔曼滤波)
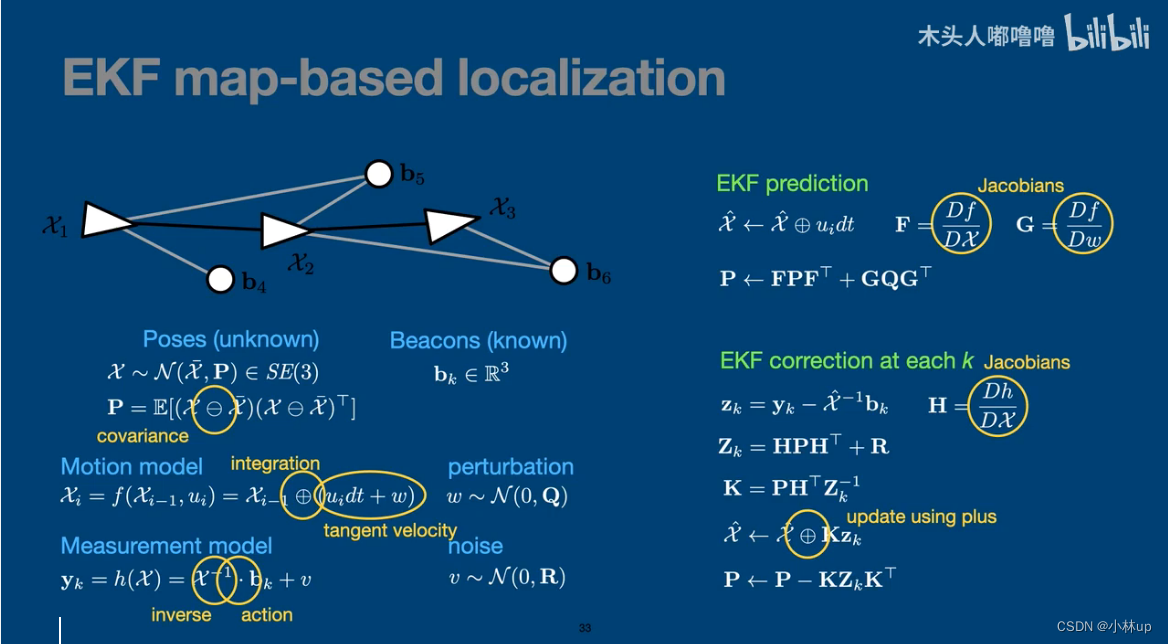
图像SLAM
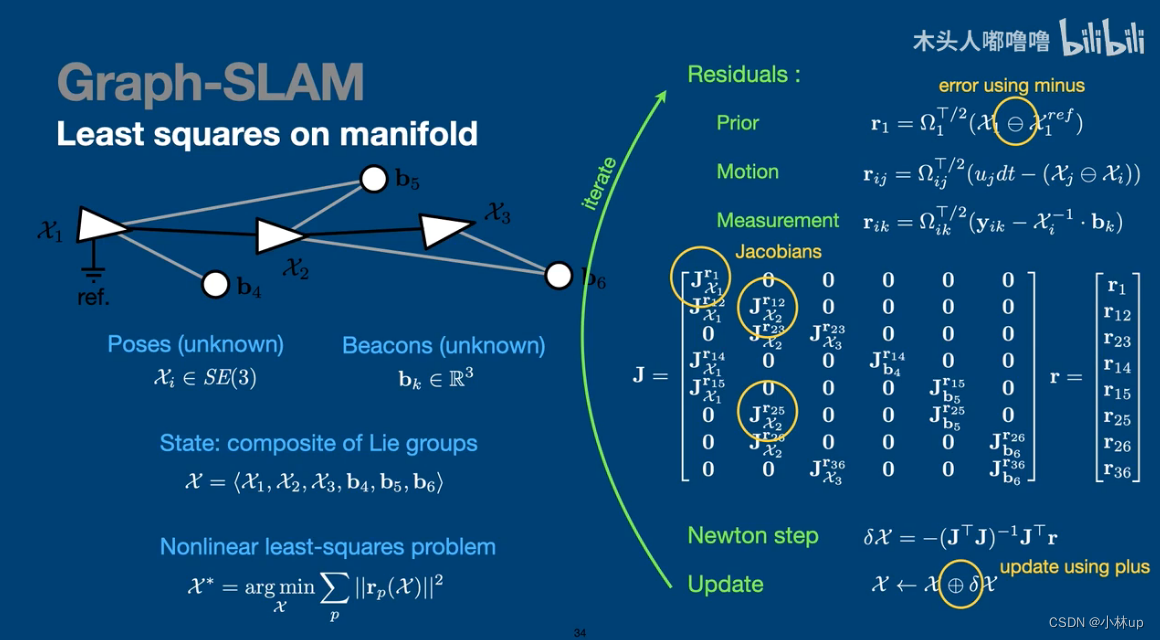
更多资料和工具

另外李群李代数相关的表(上图的第三个资料),可以查看Lie theory cheat sheet或者在我上传的资源中下载。
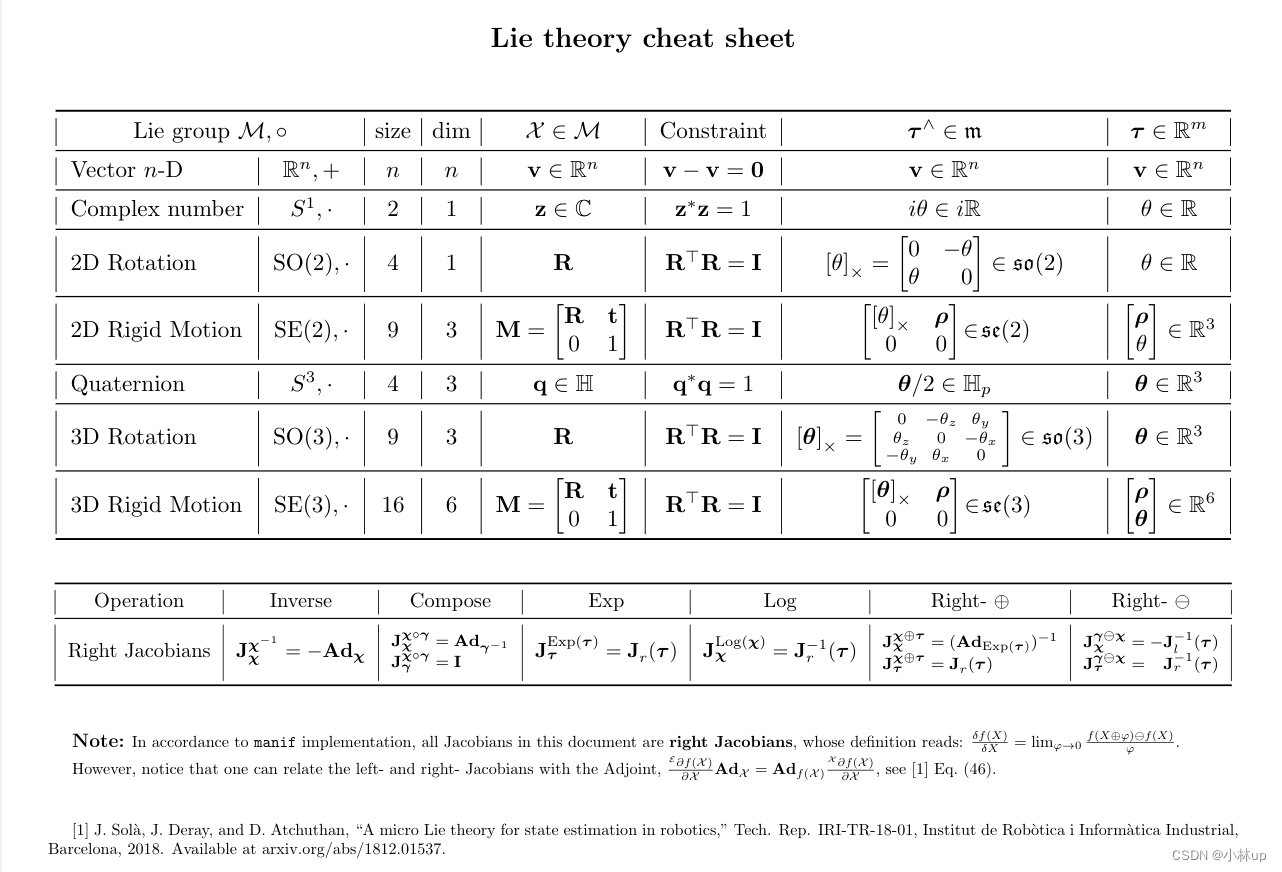
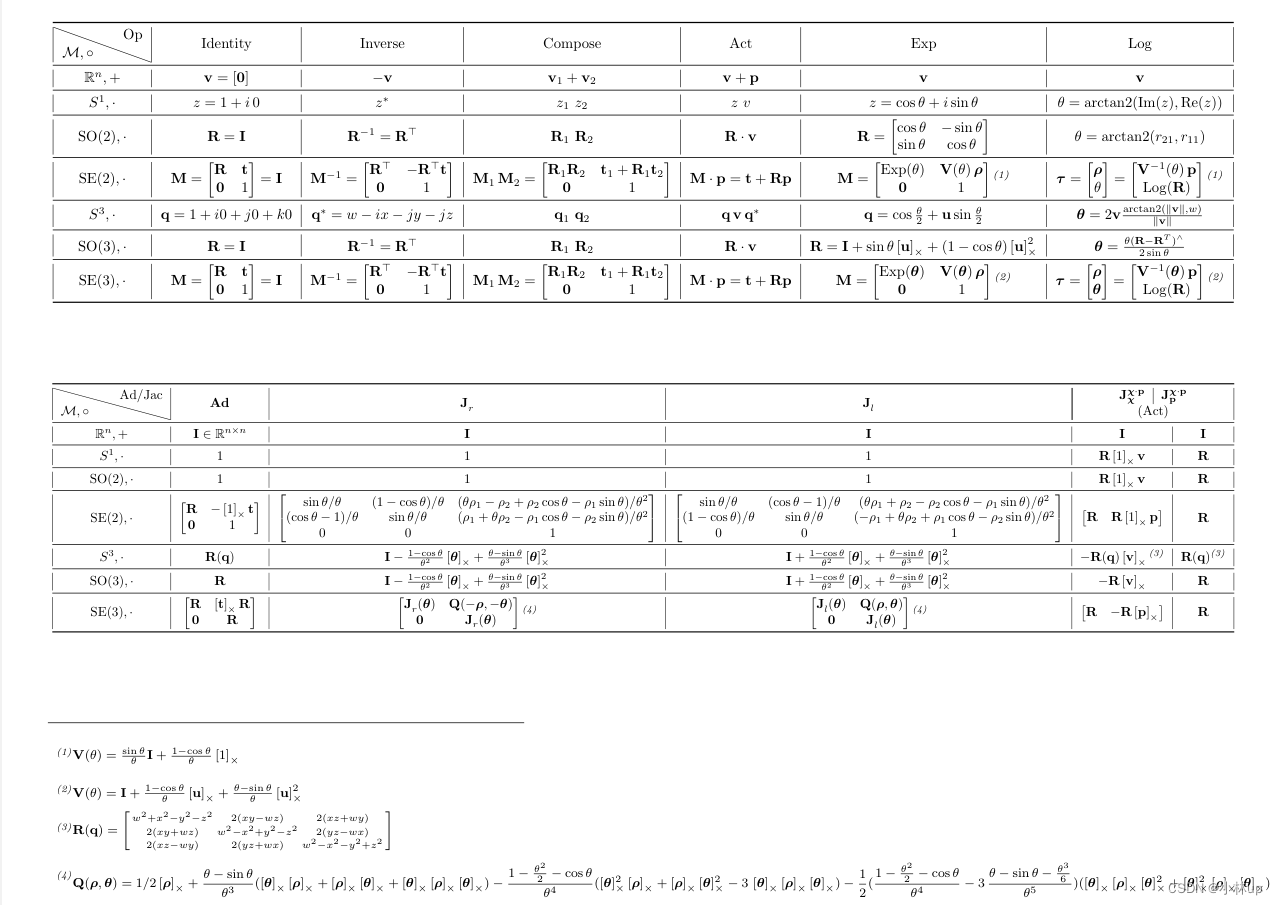
给出的其他的参考资料:
[1]A micro Lie theory for state estimation in robotics https://arxiv.org/pdf/1812.01537.pdf
[2]manif - A small header-only C++ & Python library for Lie theory https://github.com/artivis/manif
[3]Lie theory for the roboticist https://www.youtube.com/watch?v=nHOcoIyJj2o