一维差分是为了解决访问一个数组中的几个区间,降低时间复杂度使用的
差分就是前缀和的逆运算(a[i]=b[1]+b[2]+…b[i])
差分的作用就是快速实现将数组部分加上一个数。
例如
给定一个数组 A 和一些查询 Li,Ri,求数组中第 Li 至第 Ri 个元素之和。
小蓝觉得这个问题很无聊,于是他想重新排列一下数组,使得最终每个查询结果的和尽可能地大。
小蓝想知道相比原数组,所有查询结果的总和最多可以增加多少?
输入格式
输入第一行包含一个整数 n。
第二行包含 n 个整数 A1,A2,⋅⋅⋅,An,相邻两个整数之间用一个空格分隔。
第三行包含一个整数 m 表示查询的数目。
接下来 m 行,每行包含两个整数 Li、Ri,相邻两个整数之间用一个空格分隔。
输出格式
输出一行包含一个整数表示答案。
数据范围
对于 30% 的评测用例,n,m≤50;
对于 50% 的评测用例,n,m≤500;
对于 70% 的评测用例,n,m≤5000;
对于所有评测用例,1≤n,m≤105,1≤Ai≤106,1≤Li≤Ri≤n。
输入样例:
5
12345
2
13
25
输出样例:
4
样例解释
原来的和为 6+14=20,重新排列为 (1,4,5,2,3) 后和为 10+14=24,增加了 4.
先分享一下这道题的做题思路:
第一步:要想求出重新排序之后的和尽量最大,就应该使得有交集的部分和最大
例如12345 区间是1-3 和2-5 ,区间2-3要加两次,其余的加一次,要想使和最大2-3区间和应该先最大,所有一开始想求他们两个之间的交集,后来发现根本没有思路求交集,转过来想到,求同一个位置被m次区间访问的次数,就是它们相交的次数。设立一个访问数组cnt[N],例如一开始区间1-3,
cnt[5]={1,1,1,0,0};之后2-5访问后cnt[5]={1,2,2,1,1}。这就是经历过两次查询后,数组中的元素在所有访问区间 中出现的次数。
这是一开始想到的统计cnt数组元素的方法,但是会超时,因为算法复杂度是o(m*区间长度)
cin >> m;
while (m --) {
cin >> i >> j;
for (int k = i; k <= j; k++) {
cnt[k]++;
}
}后面想到了y总的一维差分方法,直接用模板
第一次询问区间1 -3
我们想得到的目标数组是 a{1,1,1,0,0,}但是时间复杂度太高了
我们用人为构造差分数组,目标数组a[i] =cnt[i]-cnt[i-1];
1 0 0 -1 0
等价于cnt[i]++;
cnt[j]--;
之后在通过差分数组可以还原得到目标数组a[5],
b[i] = cnt[i]+b[i - 1];
b[1]=cnt[1]+b[0]=1
b[2]=cnt[2]+b[1]=1
b[3]=cnt[3]+b[2]=1
b[4]=cnt[4]+b[3]=0
b[5]=cnt[5]+b[4]=1
代码如下:
while (m--) {
cin >> i >> j;
cnt[i]++;
cnt[j + 1]--;
}
for (int i = 1; i <= n; i++) {
b[i] = cnt[i]+b[i - 1];
cout << b[i] << ",";
suma = suma + a[i] * b[i];
}
第二步:求出来每个位置被访问的次数后,我想要把最大的数想要放在对应的b数组中,即访问次数最多的位置
例如原数组1 2 3 4 5
访问区间 1-3 和2-5
b数组 1 2 2 1 1,想要让最大的数4和5 去到第二个第三个位置这样求出来的和最大
也就是cnt值最大的对应原数组最大的数,这样求出来的和才最大
因此把两个数组排序
1 2 3 4 5
1 1 1 2 2
这样对应乘积累加才最大
sort(b + 1, b + n + 1);
sort(a + 1, a + 1 + n);
for (int i = 1; i <= n; i++) {
sumb = sumb + a[i] * b[i];
}最后别忘了相减,因为求的是增加了的值。
全部代码:
#include<iostream>
#include<algorithm>
using namespace std;
int i, j;
int n, m;
long long a[100005], cnt[100005],b[100005];
long long suma;
long long sumb;
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
cin >> m;
while (m--) {
cin >> i >> j;
cnt[i]++;
cnt[j + 1]--;
}
for (int i = 1; i <= n; i++) {
b[i] = cnt[i]+b[i - 1];
cout << b[i] << ",";
suma = suma + a[i] * b[i];
}
sort(b + 1, b + n + 1);
sort(a + 1, a + 1 + n);
for (int i = 1; i <= n; i++) {
sumb = sumb + a[i] * b[i];
}
cout<<endl;
cout << sumb-suma;
return 0;
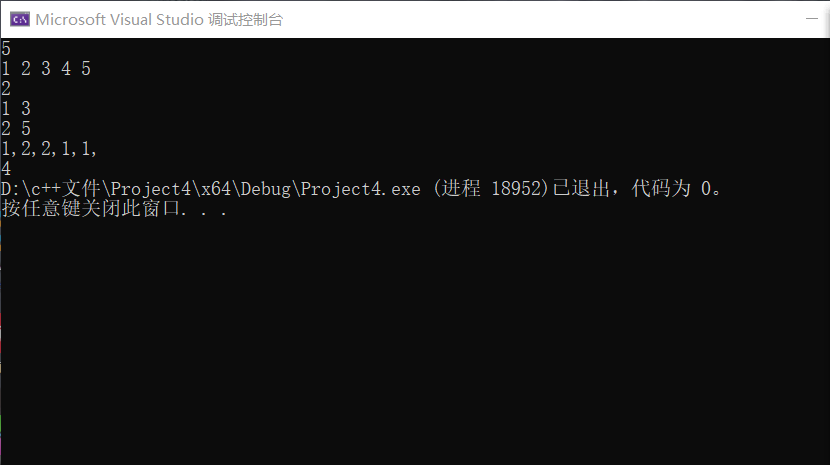
}截图: