OpenSceneGraph几何基础教程【OSG】

默认情况下，OSG 使用顶点数组法和显示列表法来渲染几何体。但是，渲染策略可能会发生变化，具体取决于几何数据的呈现方式。在本文中，我们将了解在 OSG 中处理几何体的基本技术。

在这里插入图片描述

OpenSceneGraph 后端的 OpenGL 使用几何图元（例如点、线、三角形和多边形面）来构建三维世界中的所有对象。

这些图元由它们的顶点指定，包括顶点坐标、法线分量、颜色数据和纹理坐标。此数据存储在特殊数组中。例如，可以通过为描述它们的对象指定顶点索引列表来形成图元。这种方法称为顶点数组法；它消除了内存中冗余顶点的存储并且具有良好的速度。

此外，OpenGL 可以使用所谓的显示列表机制。在显存中准备好的图元可以重复使用，这大大加快了静态对象的显示速度。

1、Geode 和 Drawable 类

osg::Geode 类标识场景树的所谓“叶”节点。它不能有子节点，但它包含渲染几何体的所有必要信息。名字 Geode 是单词 geometry node 的缩写。

引擎要处理的几何数据被记录在 osg::Drawable类的一组对象中，由 osg::Geode类管理。 osg::Drawable 类是一个纯虚类。它继承了一些子类，这些子类是通过OpenGL管线处理的三维模型、图像和文本。 OSG 中的 drawable 是指引擎可以绘制的所有元素。

osg::Geode 类提供了许多用于附加和分离可绘制对象的方法：

公共方法 addDrawable () - 将指向可绘制元素的指针传递给类 osg::Geode 的实例。所有这些元素都由智能指针 osg::ref_ptr <> 控制。

公共方法 removeDrawable () 和 removeDrawables () 从 osg::Geode 中移除对象并减少对它的引用计数。 removeDrawable() 方法将一个指向感兴趣元素的指针作为其唯一参数， removeDrawables() 方法有两个参数：初始索引和要从 osg::Geode 对象数组中移除的元素数。

getDrawable () 方法返回指向作为参数传递的索引处的元素的指针。

getNumDrawables() 方法返回附加到 osg::Geode 的元素总数。例如，要从 osg::Geode 中删除所有元素，可以使用这样的代码：

geode->removeDrawables(0, geode->getNumDrawables());

2、绘制最简单的形状

OSG提供了 osg::ShapeDrawable类，它派生自 osg::Drawable类，旨在创建最简单的三维图元。这个类包括一个 osg::Shape 对象，它存储了关于特定几何体和更多参数的信息。使用 setShape() 方法生成图元，例如：

shapeDrawable->setShape(new osg::Box(osg::Vec3(1.0f, 0.0f, 0.0f), 10.0f, 10.0f, 5.0f));

上面的代码创建一个长方体，其几何中心位于点 (1.0, 0.0, 0.0)，宽度和高度均为 10，深度为 5 个单位。 osg::Vec3 类定义了三维空间中的向量，类似的，osg::Vec2 和osg::Vec4 类描述了相应维度的向量。

OSG 中最流行的原语由类 osg::Box、 osg::Capsule 、 osg::Cone、 osg::Cylinder 和 osg::Sphere 表示。

考虑这种机制的一个例子。

#ifndef     MAIN_H
#define     MAIN_H
#include<osg/ShapeDrawable>
#include<osg/Geode>
#include<osgViewer/Viewer>
#endif
// MAIN_H

#include"main.h"

int main(int argc, char *argv[]){
    (void) argc;
    (void) argv;
    
    osg::ref_ptr<osg::ShapeDrawable> shape1 = new osg::ShapeDrawable;
    shape1->setShape(new osg::Box(osg::Vec3(-3.0f, 0.0f, 0.0f), 2.0f, 2.0f, 1.0f));
    
    osg::ref_ptr<osg::ShapeDrawable> shape2 = new osg::ShapeDrawable;
    shape2->setShape(new osg::Cone(osg::Vec3(0.0f, 0.0f, 0.0f), 1.0f, 1.0f));
    shape2->setColor(osg::Vec4(0.0f, 1.0f, 0.0f, 1.0f));
    
    osg::ref_ptr<osg::ShapeDrawable> shape3 = new osg::ShapeDrawable;
    shape3->setShape(new osg::Sphere(osg::Vec3(3.0f, 0.0f, 0.0f), 1.0f));
    shape3->setColor(osg::Vec4(0.0f, 0.0f, 1.0f, 1.0f));
    
    osg::ref_ptr<osg::Geode> root = new osg::Geode;
    root->addDrawable(shape1.get());
    root->addDrawable(shape2.get());
    root->addDrawable(shape3.get());
    
    osgViewer::Viewer viewer;
    viewer.setSceneData(root.get());
    
    return viewer.run();
}

这个例子不需要任何注释：程序创建了三个简单的形状，编译运行后，我们会看到这个结果。

在这里插入图片描述

示例中显示的机制简单明了，但它不是创建几何体的最有效方法，可以专门用于测试。要在基于 OSG 的高性能应用程序中创建几何图形，可以使用 osg::Geometry 类。

3、几何数据存储

osg::Array 类是一个基本的抽象类，从中继承了几个后代，用于存储传递给 OpenGL 函数的数据。使用此类类似于使用标准 C++ 库中的 std::vector。以下代码说明了使用 push_back() 方法将向量添加到顶点数组

vertices->push_back(osg::Vec3(1.0f, 0.0f, 0.0f));

OSG 数组在堆中分配并由智能指针控制。但是，这不适用于数组元素，例如 osg::Vec3 或 osg::Vec2，它们也可以在堆栈上创建。

osg::Geometry 类是对处理顶点数组的 OpenGL 函数的包装。它派生自 osg::Drawable 类，可以很容易地添加到 osg::Geode 对象列表中。此类将上述数组作为输入，并使用它们使用 OpenGL 生成几何图形。

4、顶点及其属性

顶点是几何图元的原子单位。它有许多描述二维或三维空间点的属性。这些属性包括：位置、颜色、法向量、纹理坐标、雾坐标等。顶点必须始终在空间中有一个位置，至于其他属性，它们可以选择性地存在。 OpenGL 支持 16 种基本的顶点属性，并且可以使用不同的数组来存储它们。

osg::Geometry类支持所有的属性数组，可以通过 set * Array()类型的方法设置。

Attribute	Data type	Osg method :: Geometry	Equivalent OpenGL call
Position	3-vector	setVertexArray ()	glVertexPointer ()
Normal	3-vector	setNormalArray ()	glNormalPointer ()
Colour	4-vector	setColorArray ()	glColorPointer ()
Secondary color	4-vector	setSecondaryColorArray ()	glSecondaryColorPointerEXT ()
Fog Coordinates	float	setFogCoordArray ()	glFogCoordPointerEXT ()
Texture coordinates	2- or 3-vector	setTexCoordArray ()	glTexCoordPointer ()
Other attributes	User defined	setVertexArribArray ()	glVertexAttribPointerARB ()

原则上，有必要为每个顶点设置属性，这会导致形成多个相同大小的属性数组 - 否则数组大小的不匹配会导致引擎出现未定义的行为。 OSG 支持各种链接顶点属性的方法，例如：

geom->setColorBinding(osg::Geometry::BIND_PER_VERTEX);

表示每个顶点和每个顶点颜色是一一对应的。但是，如果你查看这段代码：

geom->setColorBinding(osg::Geometry::BIND_OVERALL);

则将一种颜色应用于整个几何体。类似地，可以通过调用 setNormalBinding()、 setSecondaryColorBinding()、 setFogCoordBinding()方法和 setVertexAttribBinding() 方法来配置其他属性之间的关系。

5、图元集合

确定顶点属性数组后的下一步是描述如何渲染顶点数据。虚类 osg::PrimitiveSet 用于控制渲染器从一组顶点生成的几何图元。 osg::Geometry类提供了几种处理几何基元集的方法：

addPrimitiveSet () - 将指向一组图元的指针传递给对象 osg::Geometry。
removePrimitiveSet() - 移除一组图元。作为参数，它采用集合的初始索引和要删除的集合数。
getPrimitiveSet () - 通过作为参数传递的索引返回一组图元。
getNumPrimitiveSets () - 返回与该几何关联的原始集的总数。

osg::PrimitiveSet类是抽象的，没有实例化，但是有几个派生类继承自它，封装了OpenGL操作的图元集，比如 osg::DrawArrays和 osg::DrawElementsUInt。

osg::DrawArrays 类使用顶点数组的几个连续元素来构造几何基元。它可以通过调用方法创建并附加到几何体。

geom->addPrimitiveSet(new osg::DrawArrays(mode, first, count));

第一个参数指定图元模式的类型，类似于对应的OpenGL图元类型：GL_POINTS、GL_LINE_STRIP、GL_LINE_LOOP、GL_LINES、GL_TRIANGLE_STRIP、GL_TRIANGLE_FAN、GL_TRIANGLES、GL_QUAD_STRIP、GL_QUADS和GL_POLYGON。

第二个和第三个参数指定顶点数组中的第一个索引以及应从中生成几何图形的顶点数。而且，OSG 不会检查指定数量的顶点是否足以构建模式指定的几何体，这会导致应用程序崩溃！

6、绘制一个彩色正方形

我们将以上所有内容作为一个简单示例来实现。

#ifndef     
MAIN_H
#define     MAIN_H
#include<osg/Geometry>
#include<osg/Geode>
#include<osgViewer/Viewer>
#endif
// MAIN_H

#include"main.h"

int main(int argc, char *argv[]){
    
    osg::ref_ptr<osg::Vec3Array> vertices = new osg::Vec3Array;
    vertices->push_back(osg::Vec3(0.0f, 0.0f, 0.0f));
    vertices->push_back(osg::Vec3(1.0f, 0.0f, 0.0f));
    vertices->push_back(osg::Vec3(1.0f, 0.0f, 1.0f));
    vertices->push_back(osg::Vec3(0.0f, 0.0f, 1.0f));
    
    osg::ref_ptr<osg::Vec3Array> normals = new osg::Vec3Array;
    normals->push_back(osg::Vec3(0.0f, -1.0f, 0.0f));
    
    osg::ref_ptr<osg::Vec4Array> colors = new osg::Vec4Array;
    colors->push_back(osg::Vec4(1.0f, 0.0f, 0.0f, 1.0f));
    colors->push_back(osg::Vec4(0.0f, 1.0f, 0.0f, 1.0f));
    colors->push_back(osg::Vec4(0.0f, 0.0f, 1.0f, 1.0f));
    colors->push_back(osg::Vec4(1.0f, 1.0f, 1.0f, 1.0f));
    
    osg::ref_ptr<osg::Geometry> quad = new osg::Geometry;
    quad->setVertexArray(vertices.get());
    quad->setNormalArray(normals.get());
    quad->setNormalBinding(osg::Geometry::BIND_OVERALL);
    quad->setColorArray(colors.get());
    quad->setColorBinding(osg::Geometry::BIND_PER_VERTEX);
    quad->addPrimitiveSet(new osg::DrawArrays(GL_QUADS, 0, 4));
    
    osg::ref_ptr<osg::Geode> root = new osg::Geode;
    root->addDrawable(quad.get());
    
    osgViewer::Viewer viewer;
    viewer.setSceneData(root.get());
    
    return viewer.run();
}

编译执行后我们会得到类似这样的结果：

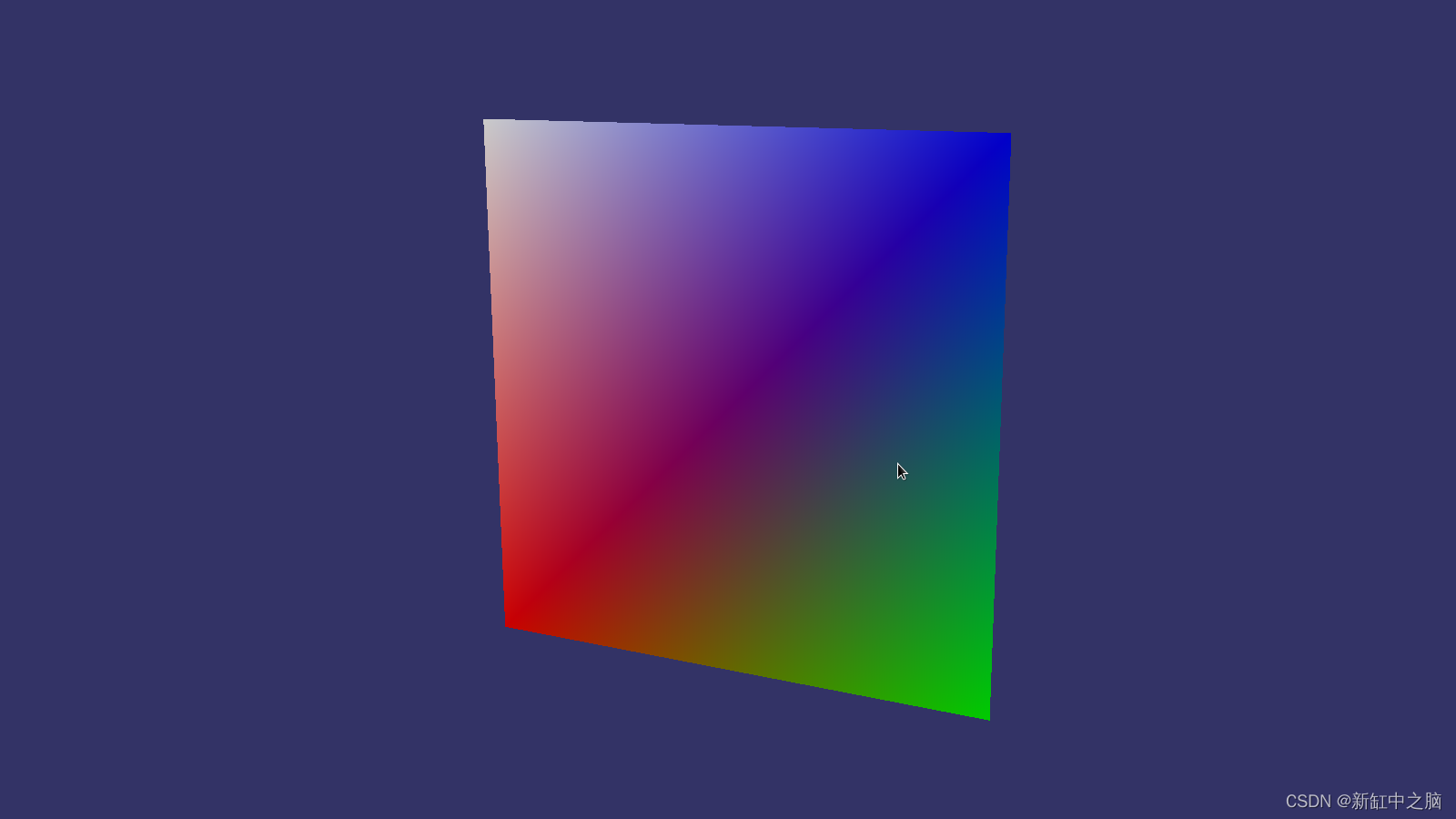
在这里插入图片描述

这个例子需要一些说明。

首先我们创建一个存储坐标的正方形顶点数组。

osg::ref_ptr<osg::Vec3Array> vertices = new osg::Vec3Array;
vertices->push_back(osg::Vec3(0.0f, 0.0f, 0.0f));
vertices->push_back(osg::Vec3(1.0f, 0.0f, 0.0f));
vertices->push_back(osg::Vec3(1.0f, 0.0f, 1.0f));
vertices->push_back(osg::Vec3(0.0f, 0.0f, 1.0f));

接下来，设置法线数组。在我们的简单案例中，我们不需要为每个顶点创建法线；描述一个垂直于正方形平面的单位向量就足够了。

osg::ref_ptr<osg::Vec3Array> normals = new osg::Vec3Array;
normals->push_back(osg::Vec3(0.0f, -1.0f, 0.0f));

为每个顶点设置颜色。

osg::ref_ptr<osg::Vec4Array> colors = new osg::Vec4Array;
colors->push_back(osg::Vec4(1.0f, 0.0f, 0.0f, 1.0f));
colors->push_back(osg::Vec4(0.0f, 1.0f, 0.0f, 1.0f));
colors->push_back(osg::Vec4(0.0f, 0.0f, 1.0f, 1.0f));
colors->push_back(osg::Vec4(1.0f, 1.0f, 1.0f, 1.0f));

现在创建一个几何对象，其中将存储我们正方形的描述，并将对其进行渲染。将顶点数组传递给此几何体。

osg::ref_ptr<osg::Geometry> quad = new osg::Geometry;
quad->setVertexArray(vertices.get());

传输法线数组，我们通知引擎所有顶点将使用单个法线，指示链接（“绑定”）法线的方法 BIND_OVAERALL：

quad->setNormalArray(normals.get());
quad->setNormalBinding(osg::Geometry::BIND_OVERALL);

相反，通过传递顶点的颜色，我们表明每个顶点都有自己的颜色：

quad->setColorArray(colors.get());
quad->setColorBinding(osg::Geometry::BIND_PER_VERTEX);

现在我们为几何创建一组图元。我们指出应该从顶点数组生成方形（GL_QUADS）面，以索引为0的顶点作为第一个顶点，顶点总数为4：

quad->addPrimitiveSet(new osg::DrawArrays(GL_QUADS, 0, 4));

好吧，几何的转移和渲染的启动：

osg::ref_ptr<osg::Geode> root = new osg::Geode;
root->addDrawable(quad.get());

osgViewer::Viewer viewer;
viewer.setSceneData(root.get());

return viewer.run();

上面的代码等效于纯 OpenGL 上的实现：

static const GLfloat vertices[][3] = { … };
glEnableClientState( GL_VERTEX_ARRAY );
glVertexPointer( 4, GL_FLOAT, 0, vertices );
glDrawArrays( GL_QUADS, 0, 4 );

7、索引图元中的顶点

osg::DrawArrays 类在直接从数组读取顶点数据时效果很好，没有间隙。但是，当同一个顶点可以属于一个对象的多个面时，它就不那么有效了。考虑这个例子：

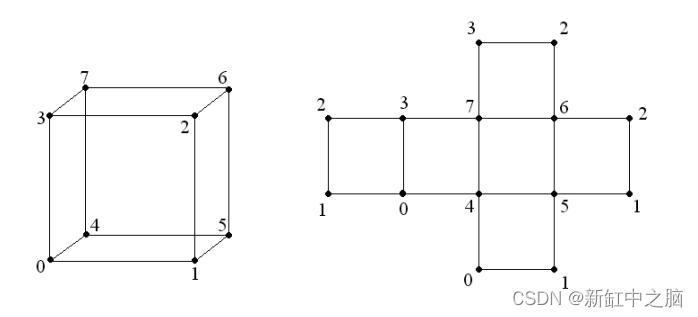
在这里插入图片描述

一个立方体有八个顶点。然而，从图中可以看出（我们正在考虑将一个立方体扫到一个平面上），一些顶点属于多个面。如果我们构建一个包含 12 个三角形面的立方体，那么这些顶点将重复，而不是 8 个顶点的数组，我们将得到 36 个顶点的数组，其中大部分实际上是相同的顶点！

在OSG中，有类 osg::DrawElementsUInt、 osg::DrawElementsUByte和 osg::DrawElementsUShort，它们使用顶点索引数组作为数据，旨在解决上述问题。索引数组存储描述几何体的面和其他元素的图元顶点的索引。将这些类应用于立方体时，存储八个顶点的数组就足够了，这些顶点通过索引数组与面相关联。

osg::DrawElements* 类型的类的设计方式与标准 std::vector 类的设计方式相同。此代码可用于添加索引。

osg::ref_ptr<osg::DrawElementsUInt> de = new osg::DrawElementsUInt(GL_TRIANGLES);
de->push_back(0); de->push_back(1); de->push_back(2);
de->push_back(3); de->push_back(0); de->push_back(2);

此代码定义图中所示的立方体的正面。

考虑另一个说明性的例子——八面体。
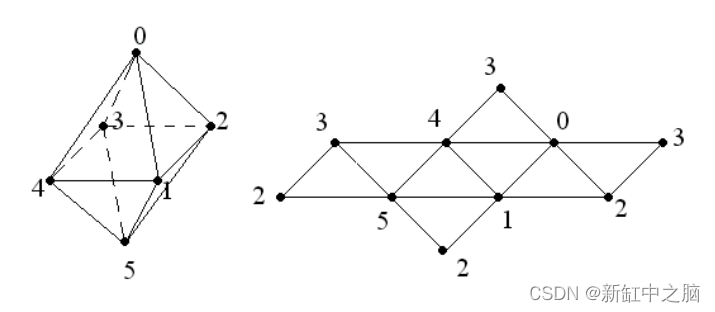
在这里插入图片描述

很有趣，因为它只包含六个顶点，但每个顶点已经在四个三角形面中了！我们可以使用 osg::DrawArrays 创建一个包含 24 个顶点的数组来显示所有八个面。然而，我们将采取不同的方式——我们将顶点存储在一个包含六个元素的数组中，并使用类 osg::DrawElementsUInt 生成面。

#ifndef     MAIN_H
#define     MAIN_H
#include<osg/Geometry>
#include<osg/Geode>
#include<osgUtil/SmoothingVisitor>
#include<osgViewer/Viewer>
#endif

#include"main.h"
int main(int argc, char *argv[]){
    
    osg::ref_ptr<osg::Vec3Array> vertices = new osg::Vec3Array(6);
    (*vertices)[0].set( 0.0f,  0.0f,  1.0f);
    (*vertices)[1].set(-0.5f, -0.5f,  0.0f);
    (*vertices)[2].set( 0.5f, -0.5f,  0.0f);
    (*vertices)[3].set( 0.5f,  0.5f,  0.0f);
    (*vertices)[4].set(-0.5f,  0.5f,  0.0f);
    (*vertices)[5].set( 0.0f,  0.0f, -1.0f);
    
    osg::ref_ptr<osg::DrawElementsUInt> indices = new osg::DrawElementsUInt(GL_TRIANGLES, 24);
    (*indices)[ 0] = 0; (*indices)[ 1] = 1; (*indices)[ 2] = 2;
    (*indices)[ 3] = 0; (*indices)[ 4] = 4; (*indices)[ 5] = 1;
    (*indices)[ 6] = 4; (*indices)[ 7] = 5; (*indices)[ 8] = 1;
    (*indices)[ 9] = 4; (*indices)[10] = 3; (*indices)[11] = 5;
    (*indices)[12] = 3; (*indices)[13] = 2; (*indices)[14] = 5;
    (*indices)[15] = 1; (*indices)[16] = 5; (*indices)[17] = 2;
    (*indices)[18] = 3; (*indices)[19] = 0; (*indices)[20] = 2;
    (*indices)[21] = 0; (*indices)[22] = 3; (*indices)[23] = 4;
    
    osg::ref_ptr<osg::Geometry> geom = new osg::Geometry;
    geom->setVertexArray(vertices.get());
    geom->addPrimitiveSet(indices.get());
    
    osgUtil::SmoothingVisitor::smooth(*geom);
    
    osg::ref_ptr<osg::Geode> root = new osg::Geode;
    root->addDrawable(geom.get());
    
    osgViewer::Viewer viewer;
    viewer.setSceneData(root.get());
    
    return viewer.run();
}

让我们对这段代码进行更详细的说明。当然首先我们创建一个有六个顶点的数组：

osg::ref_ptr<osg::Vec3Array> vertices = new osg::Vec3Array(6);
(*vertices)[0].set( 0.0f,  0.0f,  1.0f);
(*vertices)[1].set(-0.5f, -0.5f,  0.0f);
(*vertices)[2].set( 0.5f, -0.5f,  0.0f);
(*vertices)[3].set( 0.5f,  0.5f,  0.0f);
(*vertices)[4].set(-0.5f,  0.5f,  0.0f);
(*vertices)[5].set( 0.0f,  0.0f, -1.0f);

我们直接初始化每个顶点，使用指针解引用操作和 operator [] 操作符寻址其坐标向量 — 别忘了 osg::Array 和 std::vector 类似。

现在我们将面创建为顶点索引列表。

osg::ref_ptr<osg::DrawElementsUInt> indices = new osg::DrawElementsUInt(GL_TRIANGLES, 24);
(*indices)[ 0] = 0; (*indices)[ 1] = 1; (*indices)[ 2] = 2; // Грань 0
(*indices)[ 3] = 0; (*indices)[ 4] = 4; (*indices)[ 5] = 1; // Грань 1
(*indices)[ 6] = 4; (*indices)[ 7] = 5; (*indices)[ 8] = 1; // Грань 2
(*indices)[ 9] = 4; (*indices)[10] = 3; (*indices)[11] = 5; // Грань 3
(*indices)[12] = 3; (*indices)[13] = 2; (*indices)[14] = 5; // Грань 4
(*indices)[15] = 1; (*indices)[16] = 5; (*indices)[17] = 2; // Грань 5
(*indices)[18] = 3; (*indices)[19] = 0; (*indices)[20] = 2; // Грань 6
(*indices)[21] = 0; (*indices)[22] = 3; (*indices)[23] = 4; // Грань 7

面将是三角形的，共有 8 个，这意味着索引列表应包含 24 个元素。面索引按顺序进入此数组：例如，面 0 由顶点 0、1 和 2 组成；面 1 - 顶点 0、4 和 1；面 2 - 顶点 4、5 和 1，依此类推。顶点按逆时针顺序列出，如果你看正面（见上图）。

接下来是要执行的下一步。我们唯一没有做的是自动生成平滑（平均）法线，我们在这个例子中通过调用 smooth 来完成：

osgUtil::SmoothingVisitor::smooth(*geom);

事实上，如果面的顶点是给定的，那么很容易计算出它的法线。在多个面会聚的顶点处，计算某个平均法线 - 将会聚面的法线相加，并将所得总和再次归一化。这些操作（以及更多！）可以由引擎本身使用 osgUtil 库中的类来执行。因此，在我们的示例中，在 *.pro 文件中，我们将向链接器添加指示以构建我们的程序并使用此库：

CONFIG(debug, debug|release) {
    TARGET = $$join(TARGET,,,_d)
		.
		.
		.    
    LIBS += -L$$OSG_LIB_DIRECTORY -losgUtild
} else {
		.
		.
		.
    LIBS += -L$$OSG_LIB_DIRECTORY -losgUtil
}

最后的结果如下：

在这里插入图片描述

要了解其工作原理，请考虑 OpenGL 管道。
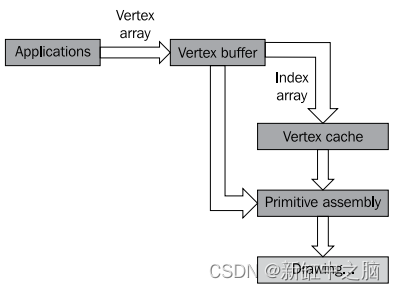
在这里插入图片描述

顶点数组机制减少了OpenGL的调用次数。它将顶点数据存储在客户端使用的应用程序的内存中。服务器端 OpenGL 管道访问各种顶点数组。如图所示，OpenGL 从客户端的顶点缓冲区中检索数据，并以有序的方式组装图元。这就是使用 osg::Geometry类的 set * Array()方法处理数据的方式。 osg::DrawArrays类直接遍历这些数组并显示出来。

使用 osg::DrawElements*时，顶点数组的维数减少，传递给管线的顶点数也减少。索引数组允许你在服务器端创建顶点缓存。 OpenGL 从缓存中读取顶点数据，而不是从客户端的顶点缓冲区中读取。这显着提高了整体渲染性能。

8、多边形网格处理技巧

OpenSceneGraph 支持用于处理场景几何对象的多边形网格的各种技术。这些预处理方法，例如多边形缩减和曲面细分，通常用于创建和优化多边形模型。它们有一个简单的界面，但是在这个过程中它们做了很多复杂的计算，不太适合即时执行。

这些技术包括：

osgUtil :: Simplifier - 减少几何中三角形的数量。公共方法 simplify() 用于简化模型的几何形状。
osgUtil :: SmootingVisitor - 法线计算。 smooth() 方法可用于为模型生成平滑法线，而不是独立计算它们并通过法线数组显式指定它们。
osgUtil :: TangentSpaceGenerator - 为模型顶点生成切线基础向量。它通过调用 generate() 方法启动，并存储 getTangentArray()、getNormalArray() 和 getBinormalArray() 方法返回的结果。在 GLSL 上编写着色器时，这些结果可用于各种顶点属性。
osgUtil :: Tesselator - 执行多边形网格的细分 - 将复杂的基元拆分为一系列简单的（retesselatePolygons () 方法）
osgUtil :: TriStripVisitor - 将几何表面转换为一组三角形面条，允许以有效的内存消耗进行渲染。 stripify() 方法根据 GL_TRIANGLE_STRIP 集将一组模型图元转换为几何图形。

所有方法都接受对象几何作为参数，通过引用 osg::Geometry&传递，例如：

osgUtil::TriStripVisitor tsv;
tsv.stripify(*geom);

其中 geom 是一个几何实例，由智能指针描述。

osg::Simplifier、 osg::SmoothingVisitor 和 osg::TriStripVisitor 类可以直接与场景图的节点一起工作，例如：

osgUtil::TriStripVisitor tsv;
node->accept(tsv);

accept()方法处理所有的子节点，直到将指定的操作应用于存储在 osg::Geode等节点中的这部分场景树的所有端节点。

让我们尝试练习细分技术。

#include"main.h"
int main(int argc, char *argv[]){
	/*
		Создаем фигуру вида
		-----
		|  _|
		| |_
		|    |
		-----
	*/
    
    osg::ref_ptr<osg::Vec3Array> vertices = new osg::Vec3Array;
    vertices->push_back( osg::Vec3(0.0f, 0.0f, 0.0f) ); // 0
    vertices->push_back( osg::Vec3(2.0f, 0.0f, 0.0f) ); // 1
    vertices->push_back( osg::Vec3(2.0f, 0.0f, 1.0f) ); // 2
    vertices->push_back( osg::Vec3(1.0f, 0.0f, 1.0f) ); // 3
    vertices->push_back( osg::Vec3(1.0f, 0.0f, 2.0f) ); // 4
    vertices->push_back( osg::Vec3(2.0f, 0.0f, 2.0f) ); // 5
    vertices->push_back( osg::Vec3(2.0f, 0.0f, 3.0f) ); // 6
    vertices->push_back( osg::Vec3(0.0f, 0.0f, 3.0f) ); // 7
    
    osg::ref_ptr<osg::Vec3Array> normals = new osg::Vec3Array;
    normals->push_back( osg::Vec3(0.0f, -1.0f, 0.0f) );
    
    osg::ref_ptr<osg::Geometry> geom = new osg::Geometry;
    geom->setVertexArray(vertices.get());
    geom->setNormalArray(normals.get());
    geom->setNormalBinding(osg::Geometry::BIND_OVERALL);
    geom->addPrimitiveSet(new osg::DrawArrays(GL_POLYGON, 0, 8));
    
    osg::ref_ptr<osg::Geode> root = new osg::Geode;
    root->addDrawable(geom.get());
    
    osgViewer::Viewer viewer;
    viewer.setSceneData(root.get());
    
    return viewer.run();
}

根据本例中顶点的空间位置，很明显我们正在尝试使用 GL_POLYGON 类型的一个面的生成来创建八个顶点的非凸多边形。构建和执行此示例显示我们预期的结果不起作用——示例显示不正确。

在这里插入图片描述

要解决此问题，应在将构建的几何体传递给查看器之前对其进行细分。

osgUtil::Tessellator ts;
ts.retessellatePolygons(*geom);

现在我们得到正确的结果。
在这里插入图片描述

上面代码的原理是什么？

一个非凸多边形，如果没有使用正确的曲面细分，将不会像我们预期的那样显示，因为寻求优化性能的 OpenGL 会将它视为一个简单的凸多边形或简单地忽略，这可能会产生完全出乎意料的结果。

类 osgUtil::Tessellator 使用算法将凸多边形转换为一系列非凸多边形 - 在我们的例子中，它将几何转换为 GL_TRIANGLE_STRIP。

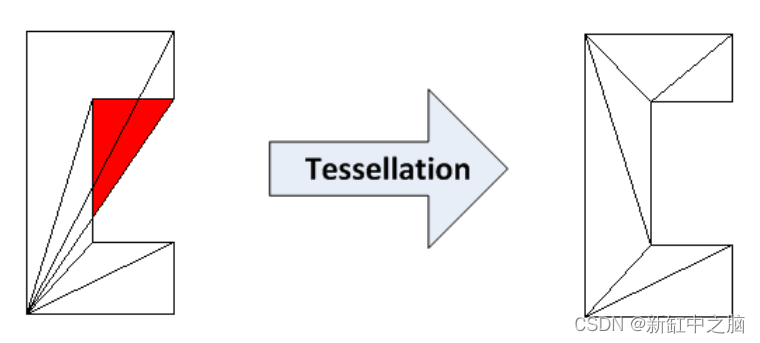
在这里插入图片描述

此类可以处理孔多边形和自相交多边形。通过公开的 setWindingType()方法，可以定义各种处理规则，如GLU_TESS_WINDING_ODD或GLU_TESS_WINDING_NONZERO，定义复杂多边形的内外区域。

9、结束语

在本文中，我们对三维物体的几何图形在 OSG 引擎中是如何存储和处理的有了基本的了解。不要认为文章中考虑的那些简单且不是很令人印象深刻的示例 - 引擎的限制。简单地说，这些示例可以帮助开发人员理解 OpenSceneGraph 的机制，如果没有这种理解，就很难想象更复杂的事情的工作。

原文链接：OSG几何开发快速教程 — BimAnt