目录
打印从1到最大的n位数
1.1 题目描述
1.2 Leetcode上的解题思路
1.3 考虑大数的问题
1.3.1 使用字符串模拟数字的加法
1.3.2 使用全排
打印从1到最大的n位数
原题链接:
剑指 Offer 17. 打印从1到最大的n位数 - 力扣(LeetCode)
1.1 题目描述
输入数字 n,按顺序打印出从 1 到最大的 n 位十进制数。比如输入 3,则打印出 1、2、3 一直到最大的 3 位数 999。
1.2 Leetcode上的解题思路
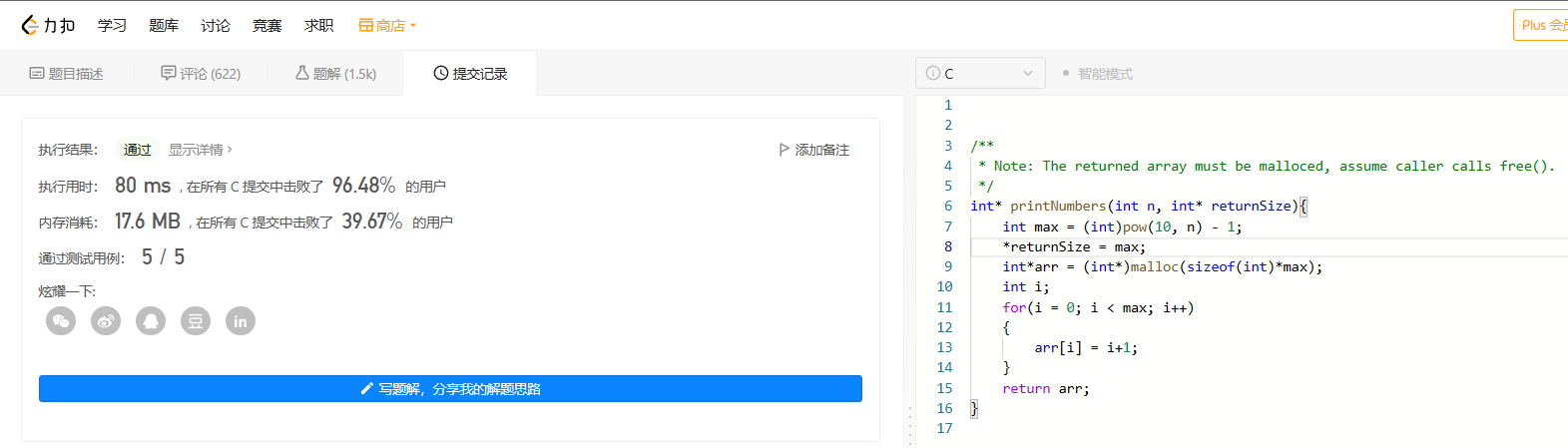
这道题目看起来很简单。我们看到这个问题之后,最容易想到的办法是先求出最大的n 位数,然后从1到最大的数赋值到数组中的对应下标即可。最大值怎么算嘞:假设输入3, 最大的三位数999 = 10 ^ 3 - 1。好的,代码如下:
int* printNumbers(int n, int* returnSize){
int max = (int)pow(10, n) - 1;
*returnSize = max;
int*arr = (int*)malloc(sizeof(int)*max);
int i;
for(i = 0; i < max; i++)
{
arr[i] = i+1;
}
return arr;
}
1.3 考虑大数的问题
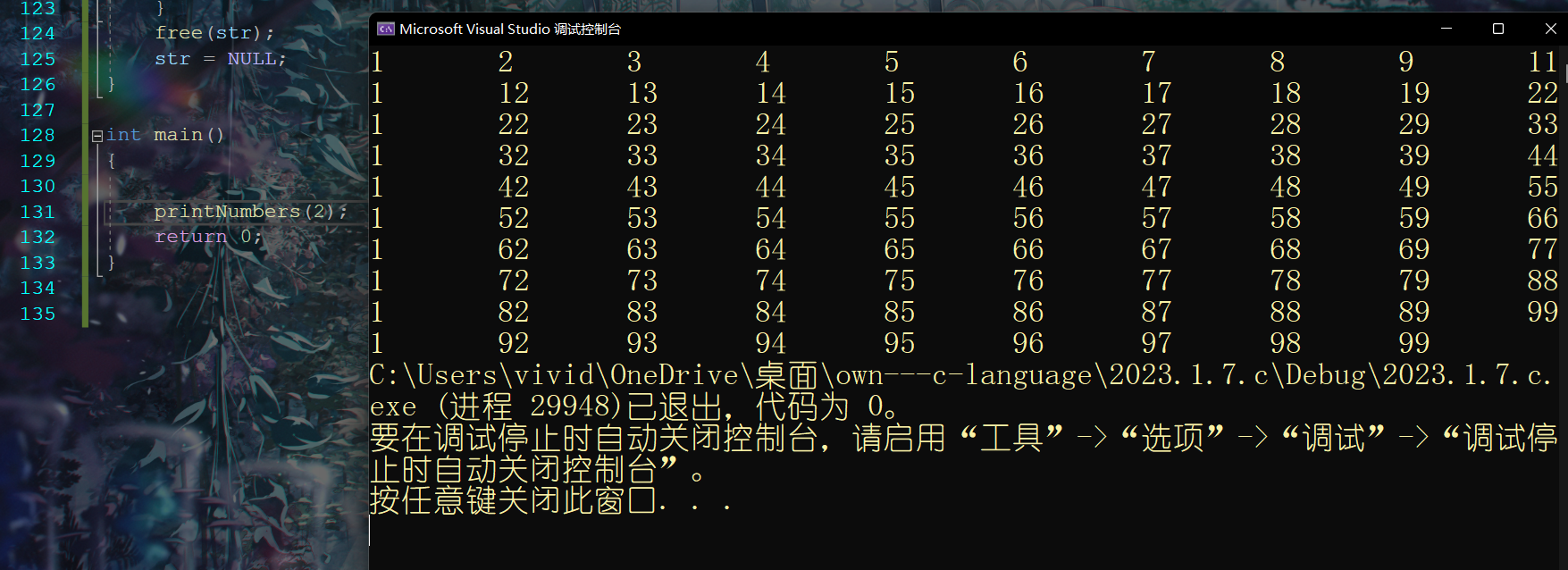
leetcode上返回的是一个int类型的数组,显然默认了数值并不会超过int类型的存储范围。但是既然是剑指offer上的题,肯定是不可能不考虑大数的问题滴。由于leetcode上无法进行测试,我就在Visual Studio 上演示结果哈!!!
1.3.1 使用字符串模拟数字的加法
在用字符串表示数字的时候,最直观的方法就是字符串里每个字符都是0'~"9"之间的某一个字符,用来表示数字中的一位。因为数字最大是n 位的,因此我们需要一个长度为n+1 的字符串(字符串中最后一位是结束符号"0')。当实际数字不够n 位的时候,在字符串的前半部分补0。首先把字符串中的每一个数字都初始化为0,然后每一次为字符串表示的数字加1,再打印出来。因此,我们只需要做两件事:
一是在字符串表达的数字上模拟加法;
二是把字符串表达的数字打印出来。
(1):在字符串表达的数字上模拟加法:(假设字符串的开头存高位)
我们需要知道什么时候停止在number上增加1,即什么时候到了最大的n 位数“999..99”(n 个9)。一个最简单的办法是在每次递增之后,都调用库函数 strcmp比较表示数字的字符串number和最大的n 位数“999..99”,如果相等则表示已经到了最大的n 位数并终止递增。虽然调用strcmp 很简单,但对于长度为 n 的字符串,它的时间复杂度为 O(n)。
我们注意到只有对“999...99”加1 的时候,才会在第一个字符(下标为0)的基础上产生进位,而其他所有情况都不会在第一个字符上产生进位。因此,当我们发现在加1 时第一个字符产生了进位,则已经是最大的n 位数,此时我们终止循环即可。
具体方法如下:

(2):将字符串表达的数字打印出来
接下来我们再考虑如何打印用字符串表示的数字。虽然库函数 printf可以很方便地打印出一个字符串,但在本题中调用 printf并不是最合适的解决方案。前面我们提到,当数字不够n位的时候,在数字的前面补0,打印的时候这些补位的0不应该打印出来。比如输入3 的时候,数字 98 用字符串表示成“098”。如果直接打印出 098,就不符合我们的阅读习惯。为此,我们定义了函数 printStr,在这个函数里,只有在碰到第一个非0 的字符之后才开始打印,直至字符串的结尾。

bool isOverflow(char* str, int n)
{
//假设没有超过
bool overflow = false;
//是否进位
int carry = 0;
for (int i = n - 1; i >= 0; i--)
{
//将字符转化为数字
int num = str[i] - '0' + carry;
//个位加1
if (i == n - 1)
{
num++;
}
//判断各位加1是否大于9
if (num > 9)
{
//加1产生进位
//判断是哪一位产生进位
if (i == 0)
{
//如果下标为0的数字产生了进位,改变overflow
overflow = true;
}
else
{
//不是下标为0的数字产生进位
num -= 10;
carry = 1; //进位1
str[i] = '0' + num; //将数字转回字符
}
}
else
{
//加1没产生进位
str[i] = '0' + num; //将数字转为字符
//加一完成后退出循环
break;
}
}
//返回判断结果
return overflow;
}
void printStr(char* str)
{
//如果指向了不为0的字符改为true,就可以继续打印啦
bool begin = false;
char* temp = str;
while (*temp)
{
if (*temp != '0' || begin)
{
begin = true;
printf("%c", *temp);
}
temp++;
}
printf("\t");
}
void printNumbers(int n)
{
//非法输入
if (n <= 0)
{
return;
}
//开辟字符串存放数字,大小为n+1个char
char* str = (char*)malloc(sizeof(char) * (n + 1));
//将字符串初始化为字符0
memset(str, '0', n);
//添加字符串的结束字符\0
str[n] = '\0';
//循环打印, 当没有超出最大的n位数继续打印
while (!isOverflow(str, n))
{
printStr(str);
}
free(str);
str = NULL;
}
int main()
{
printNumbers(2);
return 0;
}
1.3.2 使用全排
上述思路虽然比较直观,但由于模拟了整数的加法,代码有点长。接下来我们换一种思路来考虑这个问题。如 果我们在数字前面补0,就会发现n位所有十进制数其实就是n个从0到n个9 的全排列。也就是说,我们把数字的每一位都从 0 到9 排列一遍,就得到 了所有的十进制数。只是在打印的时候,排在前面的0不打印出来罢了。
全排列用递归很容易表达,数字的每一位都可能是0~9 中的一个数, 然后设置下一位。递归结束的条件是我们已经设置了数字的最后一位。
此递归函数的作用是,首先排列最高位(最高位依然下标为0),排列最高位的时候递归进到下标为1的位置进行排列,进到下标为1的位置时,同样递归到下标为2的位置进行排列,以此类推直到满足递归结束的条件,递去归来的过程不理解还是画图哈!这道题还是比较简单的。
void printStr(char* str)
{
//如果指向了不为0的字符改为true,就可以继续打印啦
bool begin = false;
char* temp = str;
while (*temp)
{
if (*temp != '0' || begin)
{
begin = true;
printf("%c", *temp);
}
temp++;
}
printf("\t");
}
void recurison(char* str, int n, int index)
{
//如果数字的排到了最高位,则结束递归
if (index == n - 1)
{
//打印此次排列好的数字
printStr(str);
return;
}
for (int i = 0; i < 10; i++)
{
//对输入的index的下一位进行1-9的全排列
str[index + 1] = i + '0';
//递归到下一位
recurison(str, n, index + 1);
}
}
void printNumbers(int n)
{
//非法输入
if (n <= 0)
{
return;
}
//开辟字符串存放数字,大小为n+1个char
char* str = (char*)malloc(sizeof(char) * (n + 1));
//添加字符串的结束字符\0
str[n] = '\0';
for (int i = 0; i < 10; i++)
{
//将数字转化为字符
str[0] = i + '0';
//进入递归尝试递归下一位
recurison(str, n, 0);
}
free(str);
str = NULL;
}
int main()
{
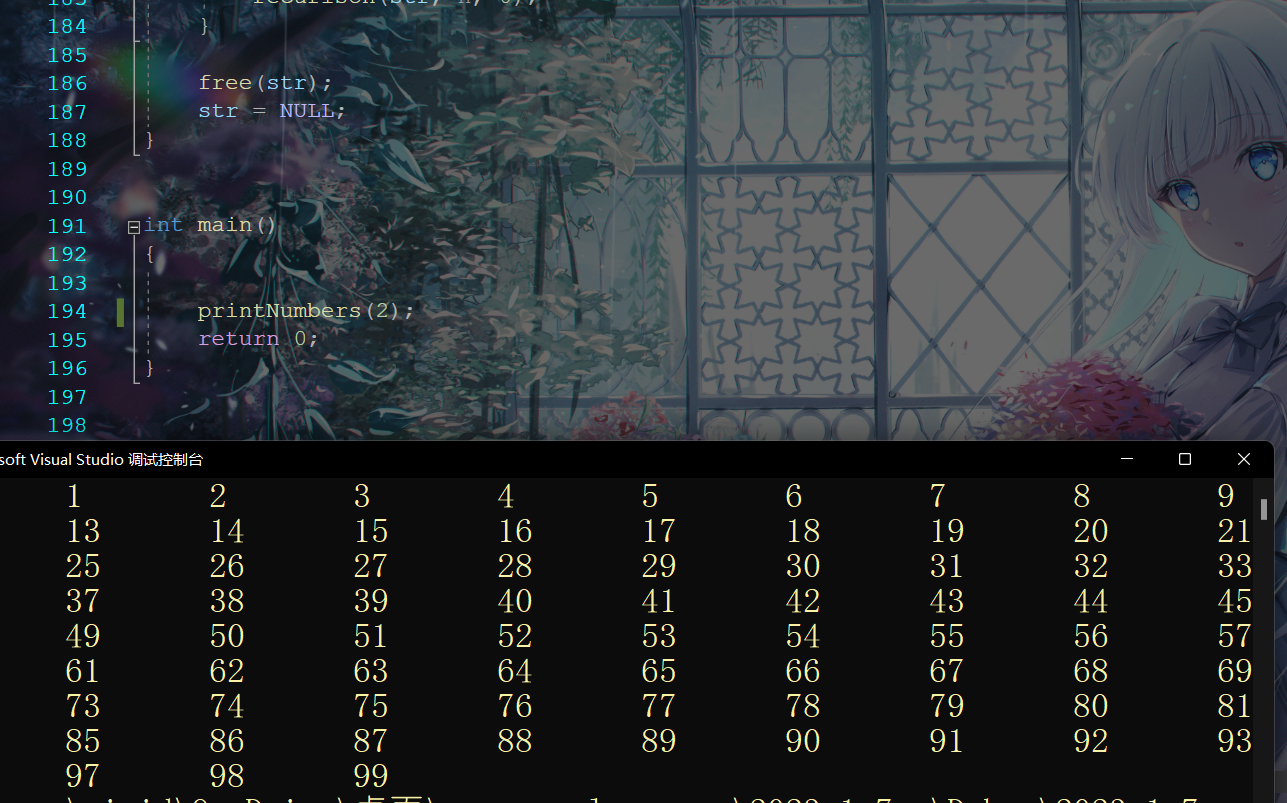
printNumbers(3);
return 0;
}