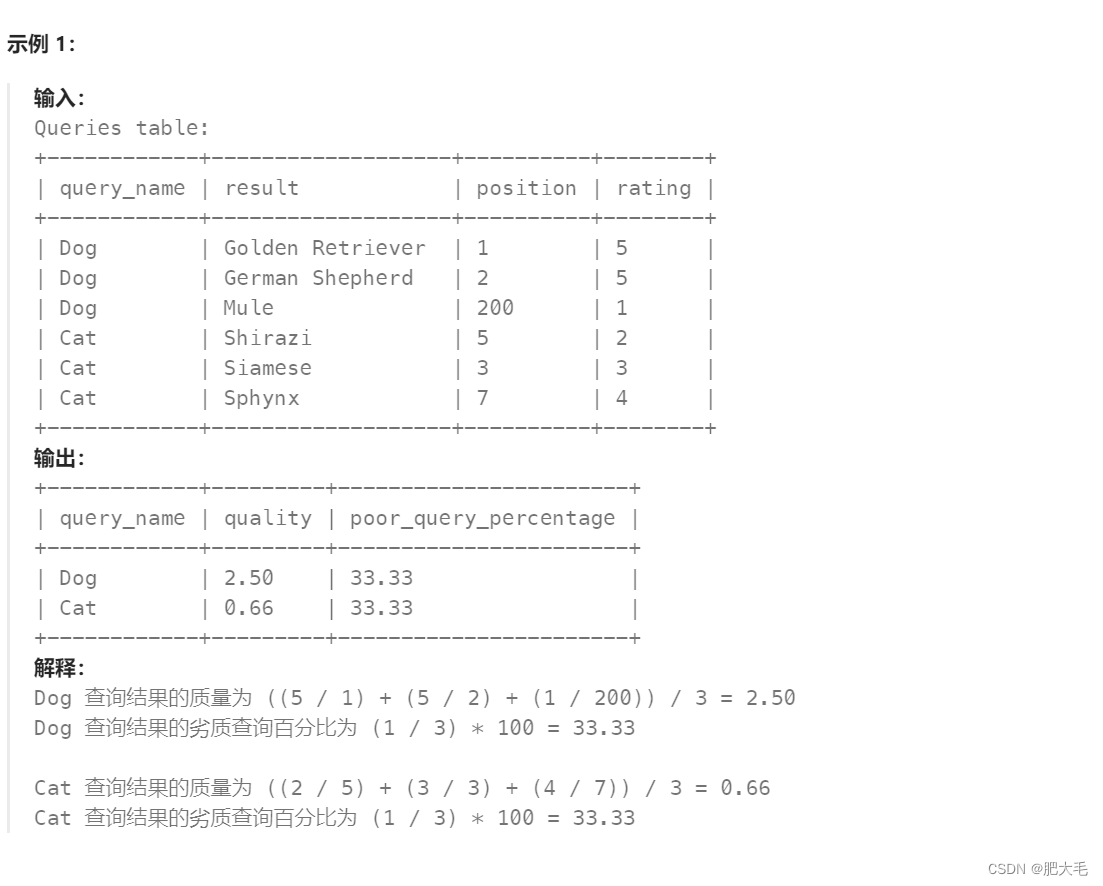
PFA,全名可溶性聚四氟乙烯,试剂瓶又叫取样瓶、样品瓶、广口瓶、储样瓶等。主要用于痕量分析、同位素分析等实验室,广泛应用于新兴的半导体、新材料、多晶硅、硅材、微电子等行业。
规格参考:30ml、60ml、100ml、125ml、250ml、300ml、500ml、1L、2L、3L、4L、5L等。

产品特点:
1、外观透明可视,材质稳定,瓶内外壁平滑,不挂壁易清洗,瓶口内壁处倒出样品时不容易有液体残留;
2、耐高温,使用温度在-200到+260度;
3、耐受强酸、强碱等强腐蚀样品,比如:魔酸、HF等以及各种有机溶剂;
4、低溶出和析出,是储存标准物质、强腐蚀性、昂贵超高纯试剂的器皿;
5、螺纹密封效果好,可长期密封存储高纯试剂及标准样品;
6、防污染:极低的金属元素空白值;










![[论文笔记] Mistral论文解读](https://img-blog.csdnimg.cn/direct/4ab32b4826344530b826f1e8295485e1.png)