我们首先要对人工智能领域有个宽泛的了解，有自己的全局性的认识，产生一些判断，才不会人云亦云地因为“薪资高、压力大”等去做出选择或者放弃。再者你做的准备调研越多，确认方向后越不容易放弃（等门槛效应）。当然，最重要还是慢慢培养兴趣，这个事情如果没有兴趣不走心，能做得很好吗？

概览

人工智能（Artificial Intelligence，AI）之研究目的是通过探索智慧的实质，扩展人类智能——促使智能主体会听（语音识别、机器翻译等）、会看（图像识别、文字识别等）、会说（语音合成、人机对话等）、会思考（人机对弈、专家系统等）、会学习（知识表示，机器学习等）、会行动（机器人、自动驾驶汽车等）。

一个经典的AI定义是：“ 智能主体可以理解数据及从中学习，并利用知识实现特定目标和任务的能力。”

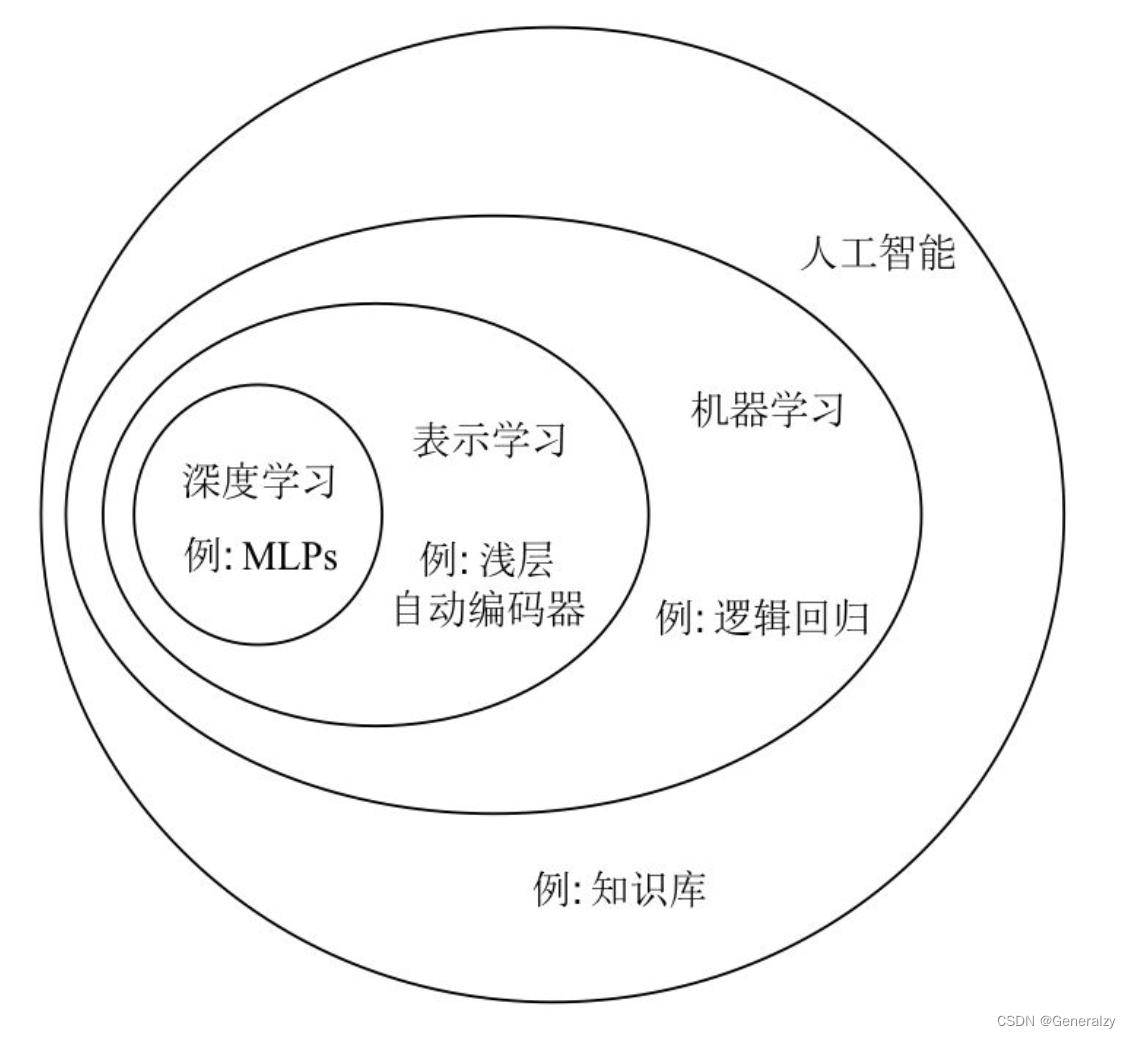
从技术层面来看，现在所说的人工智能技术基本上就是机器学习方面的（也就是，机器学习技术是入门AI的核心技术）。

机器学习是指非显式的计算机程序可以从数据中学习，以此提高处理任务的水平。
机器学习常见的任务有分类任务（如通过逻辑回归模型判断邮件是否为垃圾邮件类）、回归预测任务（线性回归模型预测房价）等等。
深度学习是机器学习的一个子方向，是当下的热门，它通过搭建深层的神经网络模型以处理任务。

从应用领域上看，人工智能在众多的应用领域上面都有一定的发展，有语言识别、自然语言处理、图像识别、数据挖掘、推荐系统、智能风控、机器人等方面。值得注意的的是，不同应用领域上，从技术层面是比较一致，但结合到实际应用场景，所需要的业务知识、算法、工程上面的要求，差别还是相当大的。

基础知识、工具准备

学习人工智能需要先掌握编程、数学方面的基本知识：AI算法工程师首先是一名程序员，掌握编程实现方法才不将容易论知识束之高阁。而数学是人工智能理论的奠基，是必不可少的。

在人工智能领域，Python使用是比较广泛的，理由如下：

1、因为其简单的语法及灵活的使用方法，Python很适合零基础入门；

2、Python有丰富的机器学习库，极大方便机器学习的开发；

3、Python在机器学习领域有较高的使用率，意味着社区庞大，应用范围广，市场上有较多的工作机会；

数学方面：数学无疑是重要的，有良好的数学基础对于算法原理的理解及进阶至关重要。但这一点对于入门的初学者反而影响没那么大，对于初学者如果数学基础比较差，有个思路是先补点“数学的最小必要知识”：如线性代数的矩阵运算；高等数学的梯度求导；概率的条件、后验概率及贝叶斯定理等等。这样可以应付大部分算法的理解。

人工智能的核心——机器学习

外部学习链接（学习路线图）

1. Python人工智能学习路线(长篇干货)
   

2. 泳鱼的github仓库：https://github.com/aialgorithm
   

3. 唐宇迪的github仓库：https://github.com/tangyudi/Ai-Learn/tree/master

以上是我在网上找到一些“免费”的学习资料与路线，无论这些大佬们是热诚开源也好还是夹带私货也罢，都给小白或初学者洒下了入门AI的一丝希冀。

于我而言，任何可以武装思想，提高能力，开拓视野的东西，都可尝试一番。

NumPy科学计算库

NumPy（Numerical Python）是Python的一种开源的数值计算扩展。提供多维数组对象，各种派生对象（如掩码数组和矩阵），这种工具可用来存储和处理大型矩阵，比Python自身的嵌套列表（nested list structure)结构要高效的多（该结构也可以用来表示矩阵（matrix）），支持大量的维度数组与矩阵运算，此外也针对数组运算提供大量的数学函数库，包括数学、逻辑、形状操作、排序、选择、输入输出、离散傅立叶变换、基本线性代数，基本统计运算和随机模拟等等。

• 几乎所有从事Python工作的数据分析师都利用NumPy的强大功能。

  • 强大的N维数组
  • 成熟的广播功能
  • 用于整合C/C++和Fortran代码的工具包
  • NumPy提供了全面的数学功能、随机数生成器和线性代数功能

• 安装Python库

  • pip install jupyter -i https://pypi.tuna.tsinghua.edu.cn/simple
  • pip install numpy -i https://pypi.tuna.tsinghua.edu.cn/simple

基本操作

数组创建

创建数组的最简单的方法就是使用array函数，将Python下的list转换为ndarray。

import numpy as np
l = [1,3,5,7,9] # 列表
arr = np.array(l) # 将列表转换为NumPy数组
arr # 数据一样，NumPy数组的方法，功能更加强大
# 输出为
# array([1, 3, 5, 7, 9])

可以利用np中的一些内置函数来创建数组，比如创建全0的数组，也可以创建全1数组，全是其他数字的数组，或者等差数列数组，正态分布数组，随机数。

import numpy as np

arr1 = np.ones(10)  # 输出为：array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])
arr2 = np.zeros(10)  # 输出为： array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])
arr3 = np.full(shape=[2, 3], fill_value=2.718)
# 输出为：
# array([[2.718, 2.718, 2.718],
#       [2.718, 2.718, 2.718]])

arr4 = np.arange(start=0, stop=20, step=2)
# 等差数列 输出为：array([ 0,  2,  4,  6,  8, 10, 12, 14, 16, 18])

arr5 = np.linspace(start=0, stop=9, num=10)
# 等差数列 输出为：array([0., 1., 2., 3., 4., 5., 6., 7., 8., 9.])

arr6 = np.random.randint(0, 100, size=10)
# int随机数 输出为：array([ 4,  8, 79, 62, 34, 35,  2, 65, 47, 18])

arr7 = np.random.randn(5)
# 正态分布 输出为：array([ 0.57807872,  0.37922855,  2.37936837, -0.28688769,  0.2882854 ])

arr8 = np.random.random(size=5)
# float 随机数 输出为：array([0.59646412, 0.37960586, 0.38077327, 0.76983539, 0.22689201])

查看数组属性

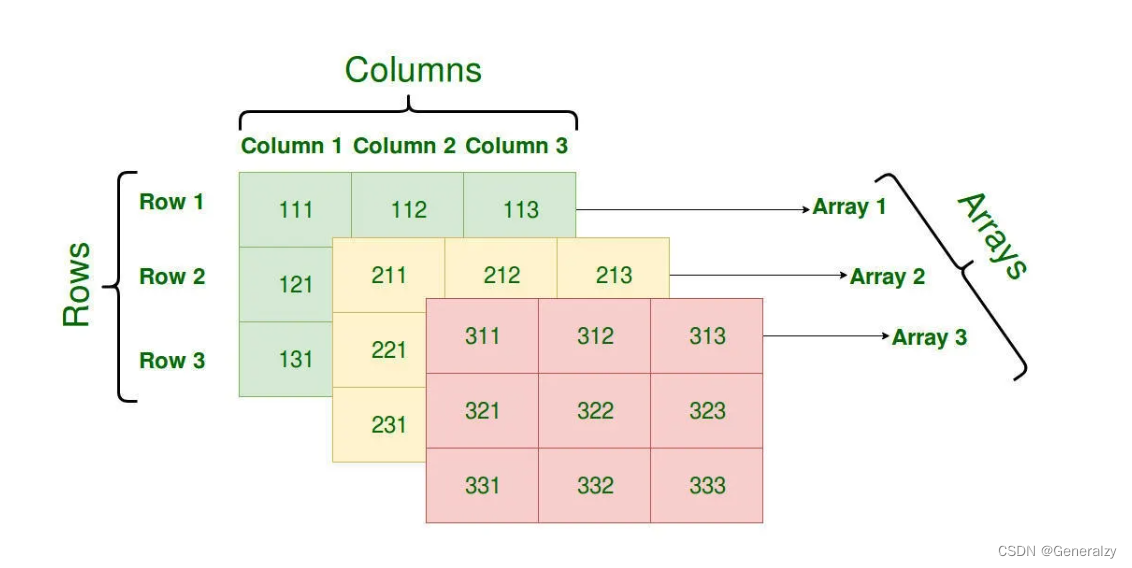
数组的轴数、维度

import numpy as np 
# 四行五列高度为3的三维数组
# def randint(low, high=None, size=None, dtype=None)
arr = np.random.randint(0,100,size = (3,4,5))
arr.ndim # 输出 3

[[[32 36 91 55 67]
  [91 18 75 60 56]
  [37 16 71 27 31]
  [85 77 53 28  0]]

 [[26 60 62  3  3]
  [89 25 11 81 40]
  [21 11 10 61 32]
  [79 36 62 48 46]]

 [[58 31 98 56 34]
  [84 12  8 12 47]
  [94 11 85 62 50]
  [66 67 44 47 81]]]

一个二维数组可以被认为是一个带有 x 行和 y 列的表格，同理一个三维数组可以看作是一个带有z个x行和y列的三维表格。 为了方便取值，z为三维数组的高，x为行，y为列，所以size为（高，行，列），对于(d)维数组n的也就是带有d个d-1维的数组。 比如size = ( 2,2,2,2)就是2个长宽高都为2的三维数组的四维数组。

数组元素的总数

import numpy as np 
arr = np.random.randint(0,100,size = (3,4,5))
arr.size # 输出 3*4*5 = 60

数据类型

import numpy as np 
arr = np.random.randint(0,100,size = (3,4,5))
arr.dtype # 输出 dtype('int64')

数组中每个元素的大小（以字节为单位）

import numpy as np 
arr = np.random.randint(0,100,size = (3,4,5))
arr.itemsize #输出是 8 ，因为数据类型是int64，64位，一个字节是8位，所以64/8 = 8

文件IO操作

保存数组

save方法保存ndarray到一个npy文件，也可以使用savez将多个array保存到一个.npz文件中

x = np.random.randn(5)
y = np.arange(0,10,1)
#save方法可以存一个ndarray
np.save("x_arr",x)
#如果要存多个数组，要是用savez方法，保存时以key-value形式保存，key任意（xarr、yarr）
np.savez("some_array.npz",xarr = x,yarr=y)

读取

load方法来读取存储的数组，如果是.npz文件的话，读取之后相当于形成了一个key-value类型的变量，通过保存时定义的key来获取相应的array

np.load('x_arr.npy') # 直接加载

# 通过key获取保存的数组数据
np.load('some_array.npz')['yarr']

读写csv、txt文件

arr = np.random.randint(0,10,size = (3,4))
#储存数组到txt文件
np.savetxt("arr.csv",arr,delimiter=',') # 文件后缀是txt也是一样的
#读取txt文件，delimiter为分隔符，dtype为数据类型
np.loadtxt("arr.csv",delimiter=',',dtype=np.int32)

数据类型

ndarray的数据类型：

• int: int8、uint8、int16、int32、int64
• float: float16、float32、float64
• str

array创建时，指定

import numpy as np
np.array([1,2,5,8,2],dtype = 'float32') 
# 输出 ：array([1., 2., 5., 8., 2.], dtype=float32)

asarray转换时指定

import numpy as np
arr = [1,3,5,7,2,9,0]
# asarray 将列表进行变换
np.asarray(arr,dtype = 'float32') 
# 输出：array([1., 3., 5., 7., 2., 9., 0.], dtype=float32)

数据类型转换astype

import numpy as np
arr = np.random.randint(0,10,size = 5,dtype = 'int16') 
# 输出：array([6, 6, 6, 6, 3], dtype=int16)
# 使用astype进行转换
arr.astype('float32') # 输出：array([1., 4., 0., 6., 6.], dtype=float32)

数组运算

加减乘除幂运算

import numpy as np
arr1 = np.array([1,2,3,4,5])
arr2 = np.array([2,3,1,5,9])
arr1 - arr2 # 减法
arr1 * arr2 # 乘法
arr1 / arr2 # 除法
arr1**arr2 # 两个星号表示幂运算
[-1 -1  2 -1 -4]
[ 2  6  3 20 45]
[0.5        0.66666667 3.         0.8        0.55555556]
[      1       8       3    1024 1953125]

如果array时二维的就会变成m*n矩阵的计算。

逻辑运算

import numpy as np
arr1 = np.array([1,2,3,4,5])
arr2 = np.array([1,0,2,3,5])
arr1 < 5
arr1 >= 5
arr1 == 5
arr1 == arr2
arr1 > arr2

数组与标量计算

数组与标量的算术运算也会将标量值传播到各个元素。

import numpy as np
arr = np.arange(1,10)
1/arr
arr+5
arr*5

*=、+=、-=操作

import numpy as np
arr1 = np.arange(5)
arr1 +=5
arr1 -=5
arr1 *=5
# arr1 /=5 不支持运算

扩展矩阵操作

由 mn 个数排成的m行n列的数表称为m行n列的矩阵，简称 mn 矩阵。记作：

这 m*n 个数称为矩阵的元素，简称为元，数aij位于矩阵 A的第i行第j列，称为矩阵 A的 (i, j) 元。

元素是实数的矩阵称为实矩阵，元素是复数的矩阵称为复矩阵。

若多个矩阵的行数和列数相同，我们称它们为同型矩阵。

行数与列数都等于n的矩阵称为n阶矩阵或n阶方阵。若多个方阵的行数（行数=列数）相同，我们称它们为同阶矩阵。

矩阵的加减法和矩阵的数乘合称矩阵的线性运算。

加法

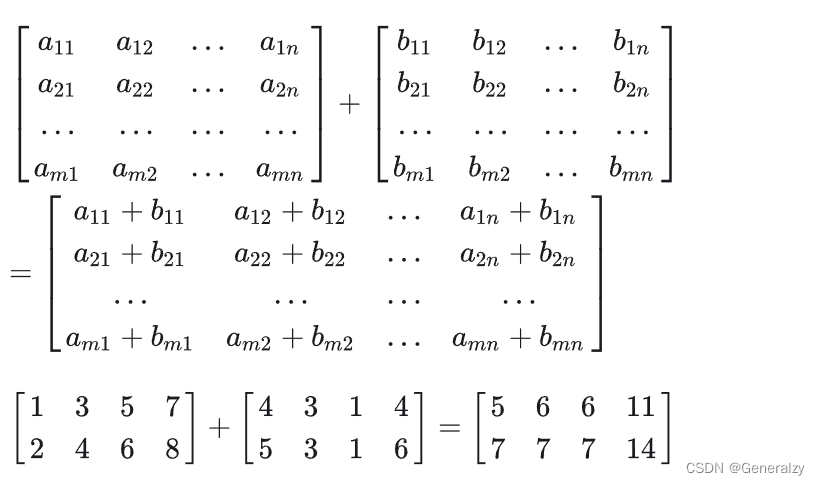
只有同型矩阵之间才可以进行加法运算，将两个矩阵相同位置的元相加即可，m行n列的两个矩阵相加后得到一个新的m行n列矩阵，例如：

交换律：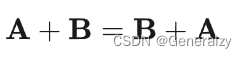

结合律：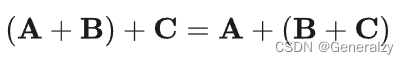

减法

与加法类似，如下：

数乘

数乘即将矩阵乘以一个常量，矩阵中的每个元都与这个常量相乘，例如：

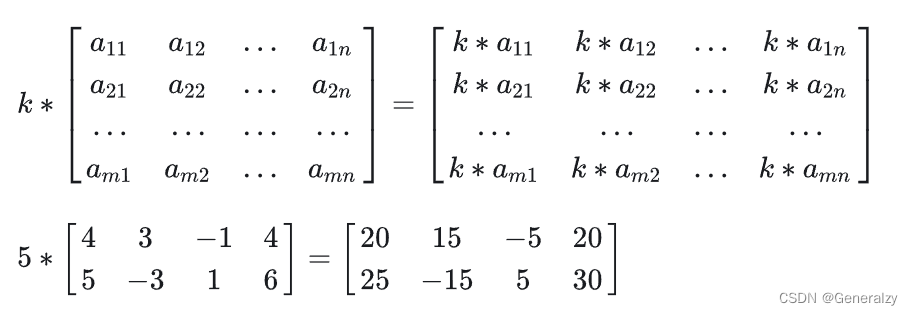
运算律:

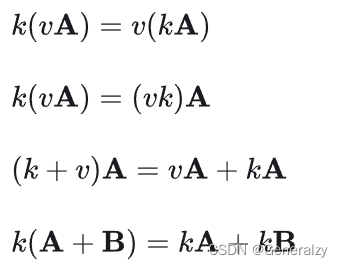
转置

把矩阵的行和列互相交换所产生的矩阵称为A的转置矩阵（标记为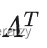
），这一过程称为矩阵的转置。

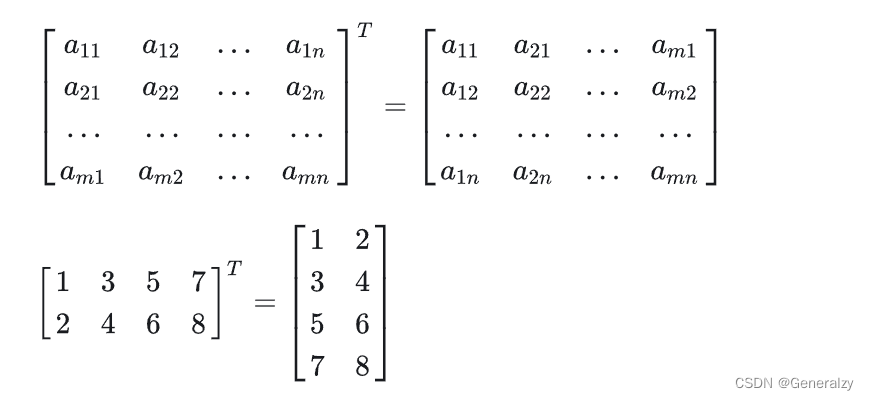
运算律：

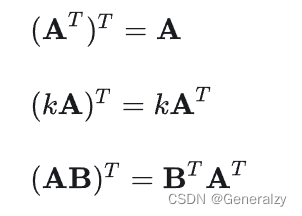
共轭

对于一个复数矩阵对其做实部不变，虚部取负的操作即为共轭操作，记作

。例如：

乘法

两个矩阵的乘法仅当第一个矩阵的列数和另一个矩阵的行数相等时才能定义，m×n 矩阵
和 n×p 矩阵相乘，会得到一个 m×p 矩阵 。

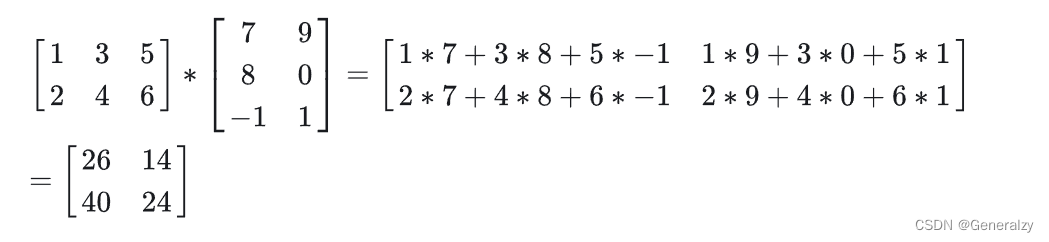
运算律：

… 其他内容需要涉猎高数，线性代数复习，（考试稳定85+的高数线代学渣感到了死去的知识的呼唤QAQ ）

array的赋值，浅拷贝，深拷贝

赋值操作只是赋值了array对象的地址值（起了个别名）：

import numpy as np
a = np.random.randint(0,100,size = (4,5))
b = a
a is b # 返回True a和b是两个不同名字对应同一个内存对象
b[0,0] = 1024 # 命运共同体

浅拷贝（新建了一个内存地址，但是引用了同一个array）：

import numpy as np
a = np.random.randint(0,100,size = (4,5))
b = a.view() # 使用a中的数据创建一个新数组对象

a is b # 返回False a和b是两个不同名字对应同一个内存对象
b.base is a # 返回True，b视图的根数据和a一样
b.flags.owndata # 返回False b中的数据不是其自己的
a.flags.owndata # 返回True a中的数据是其自己的
b[0,0] = 1024 # a和b的数据都发生改变

深拷贝（完全在内存中复制一份）：

import numpy as np
a = np.random.randint(0,100,size = (4,5))
b = a.copy()
b is a # 返回False
b.base is a # 返回False
b.flags.owndata # 返回True
a.flags.owndata # 返回True
b[0,0] = 1024 # b改变，a不变，分道扬镳

copy应该在不再需要原来的数组情况下，切片后调用。例如，假设a是一个巨大的中间结果，而最终结果b仅包含的一小部分a，则在b使用切片进行构造时应制作一个深拷贝：

import numpy as np
a = np.arange(1e8)
b = a[::1000000].copy() # 每100万个数据中取一个数据
del a # 不在需要a，删除占大内存的a
b.shape # shape(100,)

索引、切片和迭代

基本索引和切片

numpy中数组切片是原始数组的视图，这意味着数据不会被复制，视图上任何数据的修改都会反映到原数组上：

arr = np.array([0,1,2,3,4,5,6,7,8,9])
arr[5] #索引 输出 5
arr[5:8] #切片输出：array([5, 6, 7])
arr[2::2] # 从索引2开始每两个中取一个 输出 array([2, 4, 6, 8])
arr[::3] # 不写索引默认从0开始，每3个中取一个 输出为 array([0, 3, 6, 9])
arr[1:7:2] # 从索引1开始到索引7结束，左闭右开，每2个数中取一个 输出 array([1, 3, 5])
arr[::-1] # 倒序 输出 array([9, 8, 7, 6, 5, 4, 3, 2, 1, 0])
arr[::-2] # 倒序 每两个取一个 输出  array([9, 7, 5, 3, 1])
arr[5:8]=12 # 切片赋值会赋值到每个元素上，与列表操作不同
temp = arr[5:8]
temp[1] = 1024
arr # 输出：array([   0,    1,    2,    3,    4,   12, 1024,   12,    8,    9])

对于二维数组或者高维数组，可以按照之前的知识来索引，当然也可以传入一个以逗号隔开的索引列表来选区单个或多个元素：

arr2d = np.array([[1,3,5],[2,4,6],[-2,-7,-9],[6,6,6]]) # 二维数组 shape(3,4)
arr2d[0,-1] #索引 等于arr2d[0][-1] 输出 5
arr2d[0,2]  #索引 等于arr2d[0][2] ==  arr2d[0][-1] 输出 5

arr2d[:2,-2:] #切片 第一维和第二维都进行切片 等于arr2d[:2][:,1:] 
arr2d[:2,1:] #切片 1 == -2 一个是正序，另个一是倒序，对应相同的位置
# 输出：
#array([[3, 5],
#       [4, 6]])

这些千奇百怪的index都是实现了getitem的行为：

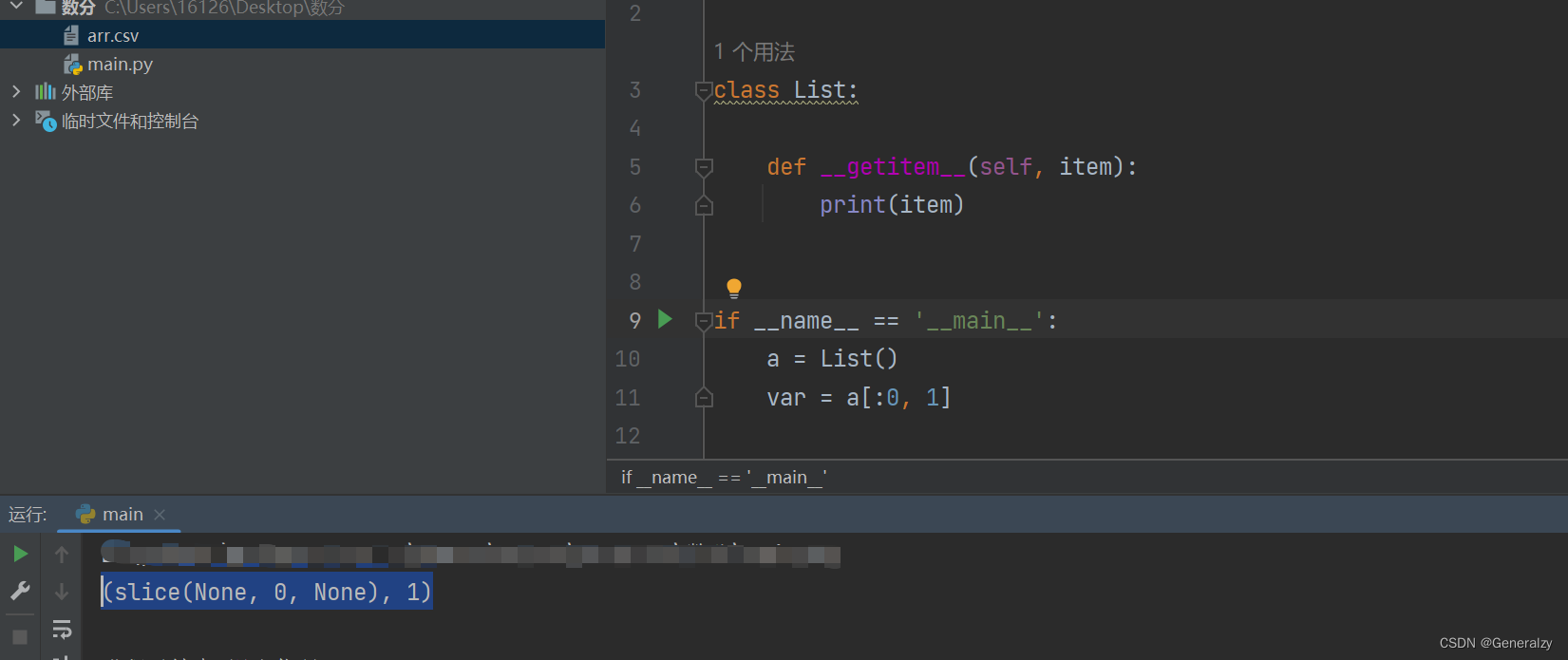
花式索引

除了传统的index索引外，numpy还支持一些花式索引：

import numpy as np
#一维
arr1 = np.array([1,2,3,4,5,6,7,8,9,10])
arr2 = arr1[[1,3,3,5,7,7,7]] # 输出 array([2, 4, 4, 6, 8, 8, 8])
arr2[-1] = 1024 # 修改值，不影响arr1
#二维
arr2d = np.array([[1,3,5,7,9],[2,4,6,8,10],[12,18,22,23,37],[123,55,17,88,103]]) #shape(4,5)
arr2d[[1,3]] # 获取第二行和第四行，索引从0开始的所以1对应第二行 
# 输出 array([[  2,   4,   6,   8,  10],
#            [123,  55,  17,  88, 103]])
arr2d[([1,3],[2,4])] # 相当于arr2d[1,2]获取一个元素,arr2d[3,4]获取另一个元素
# 输出为 array([  6, 103])
# 选择一个区域
arr2d[np.ix_([1,3,3,3],[2,4,4])] # 相当于 arr2d[[1,3,3,3]][:,[2,4,4]]
arr2d[[1,3,3,3]][:,[2,4,4]]
# ix_()函数可用于组合不同的向量
# 第一个列表存的是待提取元素的行标，第二个列表存的是待提取元素的列标
# 输出为
# array([[  6,  10,  10],
#        [ 17, 103, 103],
#        [ 17, 103, 103],
#        [ 17, 103, 103]])

boolean值索引：

names = np.array(['softpo','Brandon','Will','Michael','Will','Ella','Daniel','softpo','Will','Brandon'])
cond1 = names == 'Will'
cond1 
# 输出array([False, False,  True, False,  True, False, False, False,  True, False])
names[cond1] # array(['Will', 'Will', 'Will'], dtype='<U7')
arr = np.random.randint(0,100,size = (10,8)) # 0~100随机数
cond2 = arr > 90 
# 找到所有大于90的索引，返回boolean类型的数组 shape(10,8)，大于返回True，否则False
arr[cond2] # 返回数据全部是大于90的

形状操作

数组变形

import numpy as np
arr1 = np.random.randint(0,10,size = (3,4,5))
arr2 = arr1.reshape(12,5) # 形状改变，返回新数组
arr3 = arr1.reshape(-1,5) # 自动“整形”，自动计算

数组转置

import numpy as np
arr1 = np.random.randint(0,10,size = (3,5)) # shape(3,5)
arr1.T # shape(5,3) 转置
arr2 = np.random.randint(0,10,size = (3,6,4)) # shape(3,6,4)
np.transpose(arr2,axes=(2,0,1)) # transpose改变数组维度 shape(4,3,6)

数组堆叠

import numpy as np
arr1 = np.array([[1,2,3]])
arr2 = np.array([[4,5,6]])
np.concatenate([arr1,arr2],axis = 0) 
# 串联合并shape(2,3) axis = 0表示第一维串联 输出为
# array([[1, 2, 3],
#        [4, 5, 6]])
np.concatenate([arr1,arr2],axis = 1) 
# shape(1,6) axis = 1表示第二维串联 输出为：array([[1, 2, 3, 4, 5, 6]])

np.hstack((arr1,arr2)) # 水平方向堆叠 输出为：array([[1, 2, 3, 4, 5, 6]])
np.vstack((arr1,arr2)) 
# 竖直方向堆叠，输出为：
# array([[1, 2, 3],
#        [4, 5, 6]])

split数组拆分

import numpy as np
arr = np.random.randint(0,10,size = (6,5)) # shape(6,5)
np.split(arr,indices_or_sections=2,axis = 0) # 在第一维（6）平均分成两份 
np.split(arr,indices_or_sections=[2,3],axis = 1) # 在第二维（5）以索引2，3为断点分割成3份

np.vsplit(arr,indices_or_sections=3) # 在竖直方向平均分割成3份
np.hsplit(arr,indices_or_sections=[1,4]) # 在水平方向，以索引1，4为断点分割成3份

广播机制

当两个数组的形状并不相同的时候，可以通过扩展数组的方法来实现相加、相减、相乘等操作，这种机制叫做广播（broadcasting）

一维数组广播

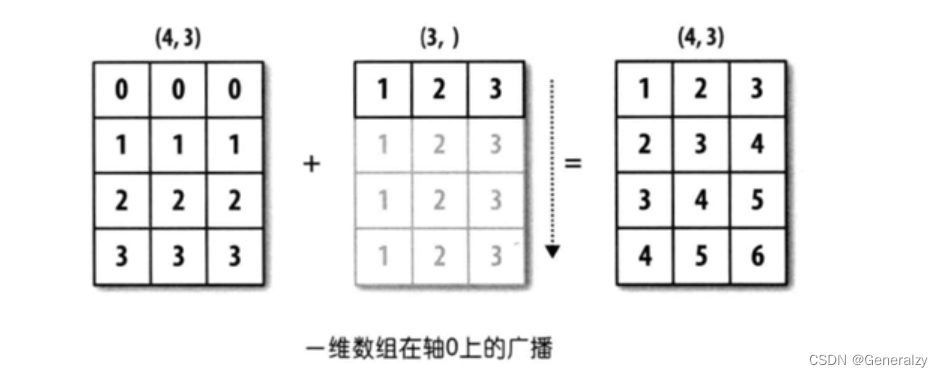
import numpy as np
arr1 = np.sort(np.array([0,1,2,3]*3)).reshape(4,3) #shape(4,3)
arr2 = np.array([1,2,3]) # shape(3,)
arr3 = arr1 + arr2 # arr2进行广播复制4份 shape(4,3)
arr3

二维数组的广播

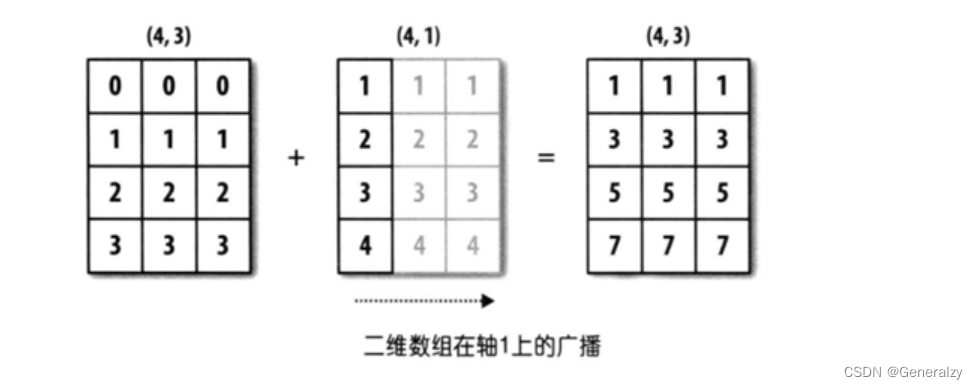
import numpy as np
arr1 = np.sort(np.array([0,1,2,3]*3)).reshape(4,3) # shape(4,3)
arr2 = np.array([[1],[2],[3],[4]]) # shape(4,1)
arr3 = arr1 + arr2 # arr2 进行广播复制3份 shape(4,3)
arr3

三维数组广播

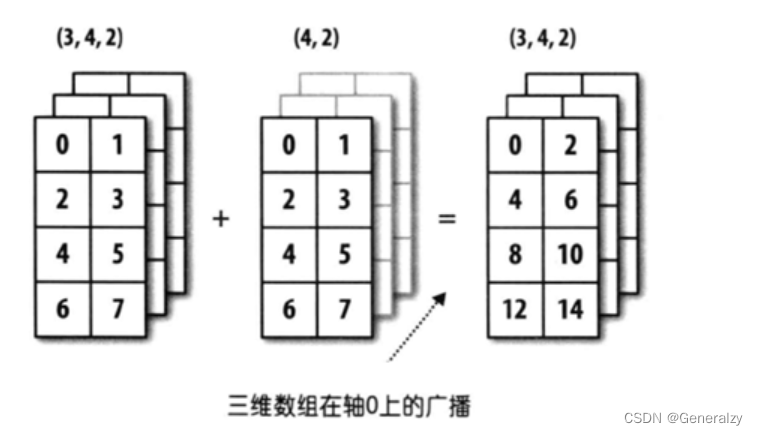
import numpy as np
arr1 = np.array([0,1,2,3,4,5,6,7]*3).reshape(3,4,2) #shape(3,4,2)
arr2 = np.array([0,1,2,3,4,5,6,7]).reshape(4,2) #shape(4,2)
arr3 = arr1 + arr2 # arr2数组在0维上复制3份 shape(3,4,2)
arr3

通用函数

数学函数

abs、sqrt、square、exp、log、sin、cos、tan，maxinmum、minimum、all、any、inner、clip、round、trace、ceil、floor

import numpy as np
arr1 = np.array([1,4,8,9,16,25])
np.sqrt(arr1) # 开平方
np.square(arr1) # 平方
np.clip(arr1,2,16) # 输出 array([ 2,  4,  8,  9, 16, 16])

x = np.array([1,5,2,9,3,6,8])
y = np.array([2,4,3,7,1,9,0])
np.maximum(x,y) # 返回两个数组中的比较大的值
arr2 = np.random.randint(0,10,size = (5,5))
np.inner(arr2[0],arr2) #返回一维数组向量内积

where函数

where 函数，三个参数，条件为真时选择值的数组，条件为假时选择值的数组

import numpy as np
arr1 = np.array([1,3,5,7,9])
arr2 = np.array([2,4,6,8,10])
cond = np.array([True,False,True,True,False])
np.where(cond,arr1,arr2) # True选择arr1，False选择arr2的值
# 输出 array([ 1,  4,  5,  7, 10])

arr3 = np.random.randint(0,30,size = 20)
np.where(arr3 < 15,arr3,-15) # 小于15还是自身的值，大于15设置成-15

排序方法

np中还提供了排序方法，排序方法是就地排序，即直接改变原数组

arr.sort()、np.sort()、arr.argsort()

import numpy as np
arr = np.array([9,3,11,6,17,5,4,15,1])
arr.sort() # 直接改变原数组
np.sort(arr) # 返回深拷贝排序结果
arr = np.array([9,3,11,6,17,5,4,15,1])
arr.argsort() # 返回从小到大排序索引 array([8, 1, 6, 5, 3, 0, 2, 7, 4])

集合运算函数

A = np.array([2,4,6,8])
B = np.array([3,4,5,6])
np.intersect1d(A,B) # 交集 array([4, 6])
np.union1d(A,B) # 并集 array([2, 3, 4, 5, 6, 8])
np.setdiff1d(A,B) #差集，A中有，B中没有 array([2, 8])

统计函数

min、max、mean、median、sum、std、var、cumsum、cumprod、argmin、argmax、argwhere、cov、corrcoef

import numpy as np
arr1 = np.array([1,7,2,19,23,0,88,11,6,11])
arr1.min() # 计算最小值 0
arr1.argmax() # 计算最大值的索引 返回 6
np.argwhere(arr1 > 20) # 返回大于20的元素的索引
np.cumsum(arr1) # 计算累加和
arr2 = np.random.randint(0,10,size = (4,5))
arr2.mean(axis = 0) # 计算列的平均值
arr2.mean(axis = 1) # 计算行的平均值
np.cov(arr2,rowvar=True) # 协方差矩阵
np.corrcoef(arr2,rowvar=True) # 相关性系数

线性代数

矩阵乘积

#矩阵的乘积
A = np.array([[4,2,3],
              [1,3,1]]) # shape(2,3)
B = np.array([[2,7],
              [-5,-7],
              [9,3]]) # shape(3,2)
np.dot(A,B) # 矩阵运算 A的最后一维和B的第一维必须一致
A @ B # 符号 @ 表示矩阵乘积运算

矩阵其他计算

下面可以计算矩阵的逆、行列式、特征值和特征向量、qr分解值，svd分解值

#计算矩阵的逆
from numpy.linalg import inv,det,eig,qr,svd
A = np.array([[1,2,3],
              [2,3,4],
              [4,5,8]]) # shape(3,3)
inv(t) # 逆矩阵
det(t)#计算矩阵行列式