---

一、58. 最后一个单词的长度

简单
给你一个字符串 s，由若干单词组成，单词前后用一些空格字符隔开。返回字符串中 最后一个 单词的长度。
单词 是指仅由字母组成、不包含任何空格字符的最大子字符串。

示例 1：
输入：s = “Hello World”
输出：5
解释：最后一个单词是“World”，长度为5。

示例 2：
输入：s = " fly me to the moon "
输出：4
解释：最后一个单词是“moon”，长度为4。

示例 3：
输入：s = “luffy is still joyboy”
输出：6
解释：最后一个单词是长度为6的“joyboy”。

class S58:
    def func(self, s):

        r = len(s) - 1

        for i in range(len(s) - 1, -1, -1):
            if s[i] == " ":
                r -= 1
            else:
                break

        l = r
        for i in range(l, -1, -1):
            if s[i] != " ":
                l -= 1
            else:
                break

        return r - l


r = S58()
s = "   fly me   to   the moon  "
print(r.func(s))

二、48. 旋转图像

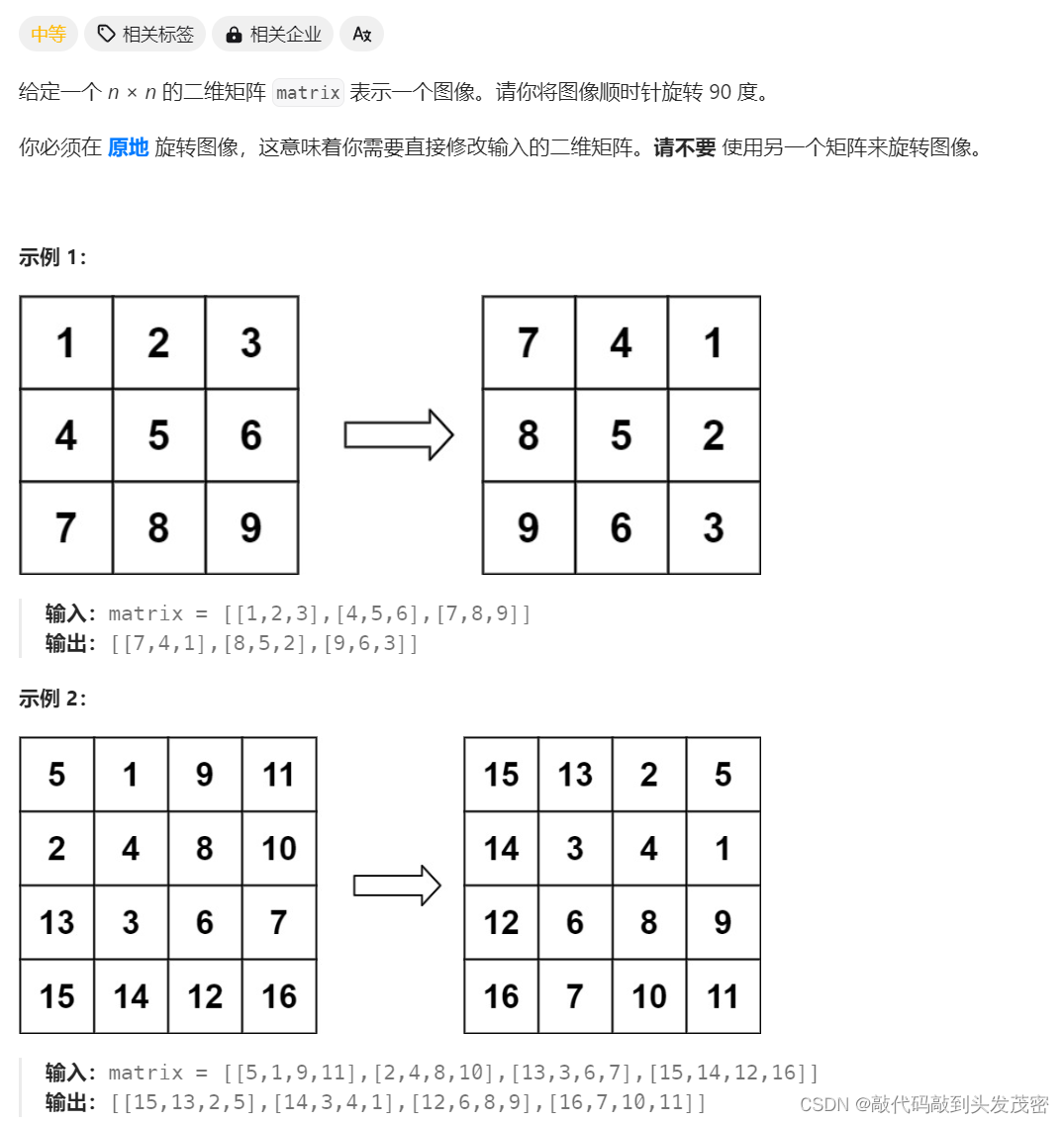
先上下反转
再按照对角线反转
本题采用上下反转
1 2 3 7 8 9
4 5 6 4 5 6
7 8 9 1 2 3
载通过主对角线进行反转
7 4 1
8 5 2
9 6 3

class S48:
    def func(self, nums):
        n = len(nums)
        i = 0
        j = n - 1
        for m in range(n):
            nums[i][m], nums[j][m] = nums[j][m], nums[i][m]

        # 对角线进行反转，对下部分进行反转
        for x in range(1, n):
            for y in range(x):
                nums[x][y], nums[y][x] = nums[y][x], nums[x][y]

        return nums


r = S48()
nums = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
print(r.func(nums))

三、69. x 的平方根

简单
给你一个非负整数 x ，计算并返回 x 的 算术平方根 。
由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去 。
注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

示例 1：
输入：x = 4
输出：2

示例 2
输入：x = 8
输出：2
解释：8 的算术平方根是 2.82842…, 由于返回类型是整数，小数部分将被舍去。

思路：二分查找

class S69:
    def func(self,x):
        left=0
        right=x     #任何数的平方根都小于本身
        ans=-1
        while left<=right:
            mid=(left+right)//2
            if mid*mid<=x:
                ans=mid
                left=mid+1
            else:
                right=mid-1
        return ans

r=S69()
x=8
print(r.func(x))

四、50. Pow(x, n)

中等
实现 pow(x, n) ，即计算 x 的整数 n 次幂函数（即，xn ）。

示例 1：
输入：x = 2.00000, n = 10
输出：1024.00000

示例 2：
输入：x = 2.10000, n = 3
输出：9.26100

示例 3：
输入：x = 2.00000, n = -2
输出：0.25000
解释：2-2 = 1/22 = 1/4 = 0.25

class S50:
    def func(self,x,n):
        if n<0:
            x=1/x
            n=-n
        res=1
        while n:
            if n%2==0:
                x=x*x
                n=n//2
            else:
                res=res*x
                n=n-1
        return res
r=S50()
x = 2.00000
n = 3
print(r.func(x, n))

---