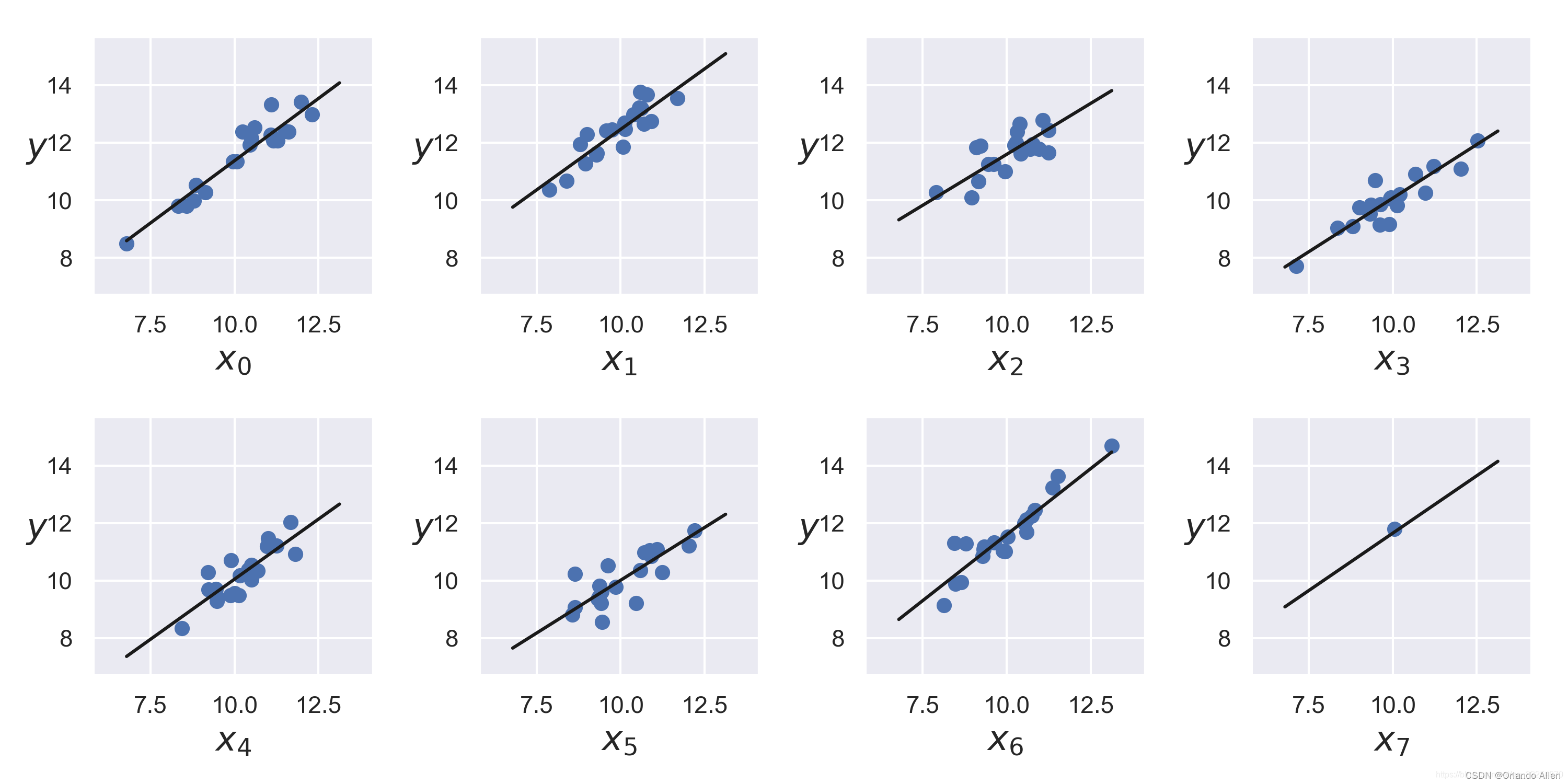
贝叶斯回归是一种统计方法,它利用贝叶斯定理来更新对回归参数的估计。这种方法不仅考虑了数据的不确定性,还考虑了模型参数的不确定性,为预测提供了一个更加全面的框架。在本文中,我们将深入探讨贝叶斯回归的基本概念、如何实现它以及它与传统回归方法之间的区别。
贝叶斯回归的基本原理
贝叶斯回归基于贝叶斯定理,这是一种计算条件概率的方法。在回归分析的背景下,条件概率用于表示在给定数据D的情况下,模型参数θ的概率。贝叶斯定理可以表达为:

实现贝叶斯回归
实现贝叶斯回归主要涉及三个步骤:选择先验分布、计算似然函数和计算后验分布。先验分布通常根据先前的知识或经验选择。似然函数根据数据和模型计算。最后,利用贝叶斯定理计算后验分布,这个分布反映了在考虑数据信息后参数的不确定性。
贝叶斯回归与传统回归的区别
贝叶斯回归和传统回归最主要的区别在于处理不确定性的方式。传统回归方法,如最小二乘回归,通常提供一个点估计,忽略了参数估计的不确定性。相比之下,贝叶斯回归提供了一个概率分布,这个分布表明了参数可能的值及其相应的不确定性水平。
此外,贝叶斯回归通过先验分布允许在分析之前引入背景知识或假设,这为模型提供了更大的灵活性。而传统回归方法通常不考虑先验知识。
应用领域
贝叶斯回归因其处理不确定性和整合先验知识的能力,在多个领域中得到了广泛应用。这些领域包括但不限于金融模型预测、生物统计学、环境科学和机器学习。
示例代码
为了给你一个贝叶斯回归的具体实例,我们将使用 Python 的 PyMC3 库。PyMC3 是一个流行的贝叶斯建模工具,它允许用户以非常直观的方式定义模型,并且利用 MCMC(Markov Chain Monte Carlo)方法进行后验分布的采样。在这个示例中,我们将创建一个简单的线性回归模型,其中参数的不确定性将通过贝叶斯方法进行估计。
import pymc3 as pm
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(123)
X = np.linspace(0, 10, 100)
slope_true = 2.5
intercept_true = 0.5
Y = slope_true * X + intercept_true + np.random.randn(100) * 2
# 使用PyMC3定义模型
with pm.Model() as model:
# 定义先验分布
intercept = pm.Normal('Intercept', mu=0, sigma=10)
slope = pm.Normal('Slope', mu=0, sigma=10)
sigma = pm.HalfNormal('sigma', sigma=1)
# 定义似然函数
likelihood = pm.Normal('Y', mu=intercept + slope * X, sigma=sigma, observed=Y)
# 进行MCMC采样
trace = pm.sample(3000, return_inferencedata=False)
pm.traceplot(trace)
plt.show()
print(pm.summary(trace))
结论
贝叶斯回归提供了一种强大的方法来处理统计分析中的不确定性问题。通过整合数据信息和先验知识,它能够提供关于模型参数的全面视角,从而使预测更加可靠。尽管贝叶斯回归的计算可能比传统方法更复杂,但其在处理复杂数据结构和不确定性方面的优势使其成为许多领域的首选方法。随着计算技术的进步和统计软件的发展,贝叶斯方法变得越来越易于实现,预计将在未来的统计分析和数据科学研究中发挥更大的作用。