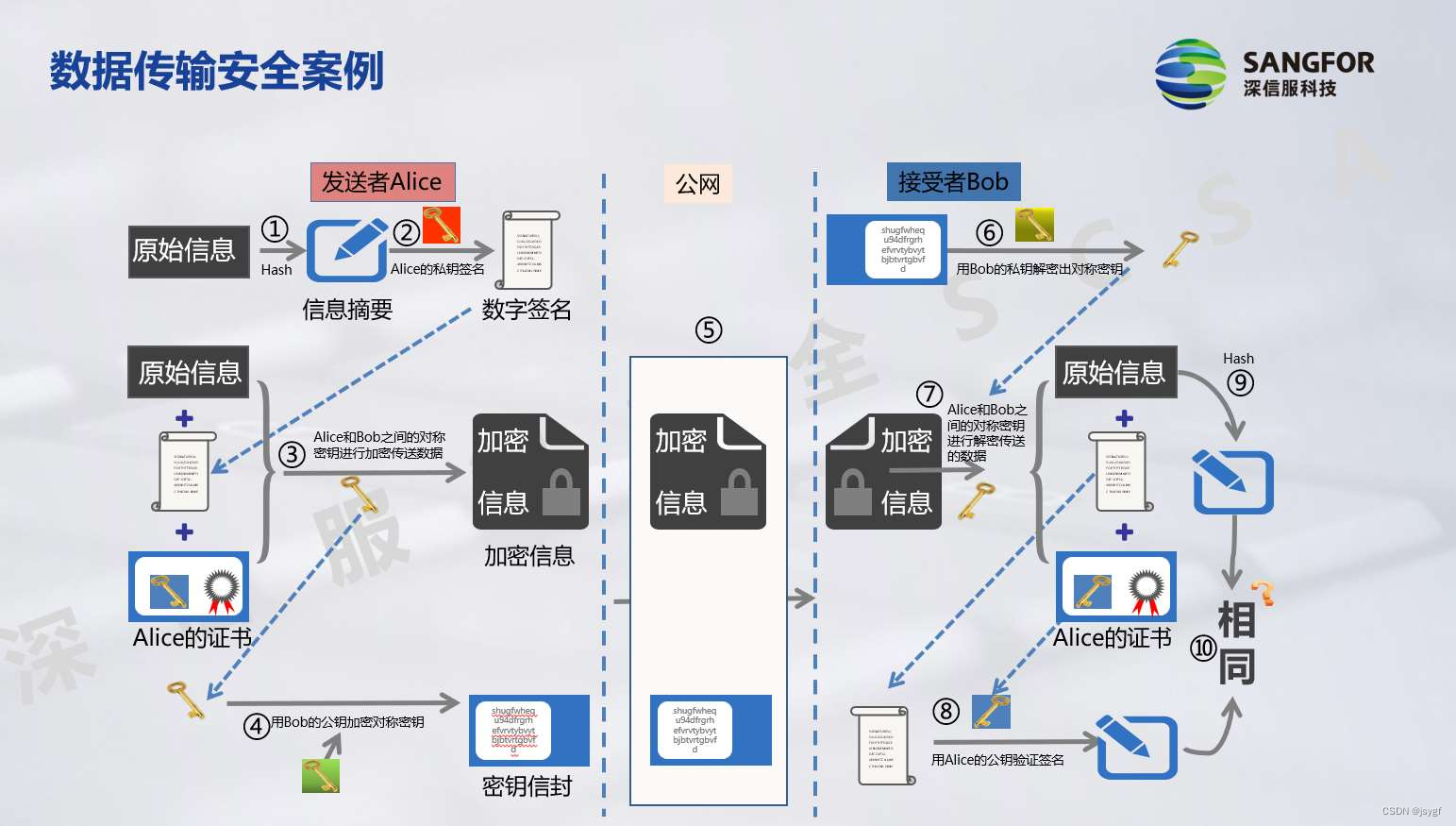
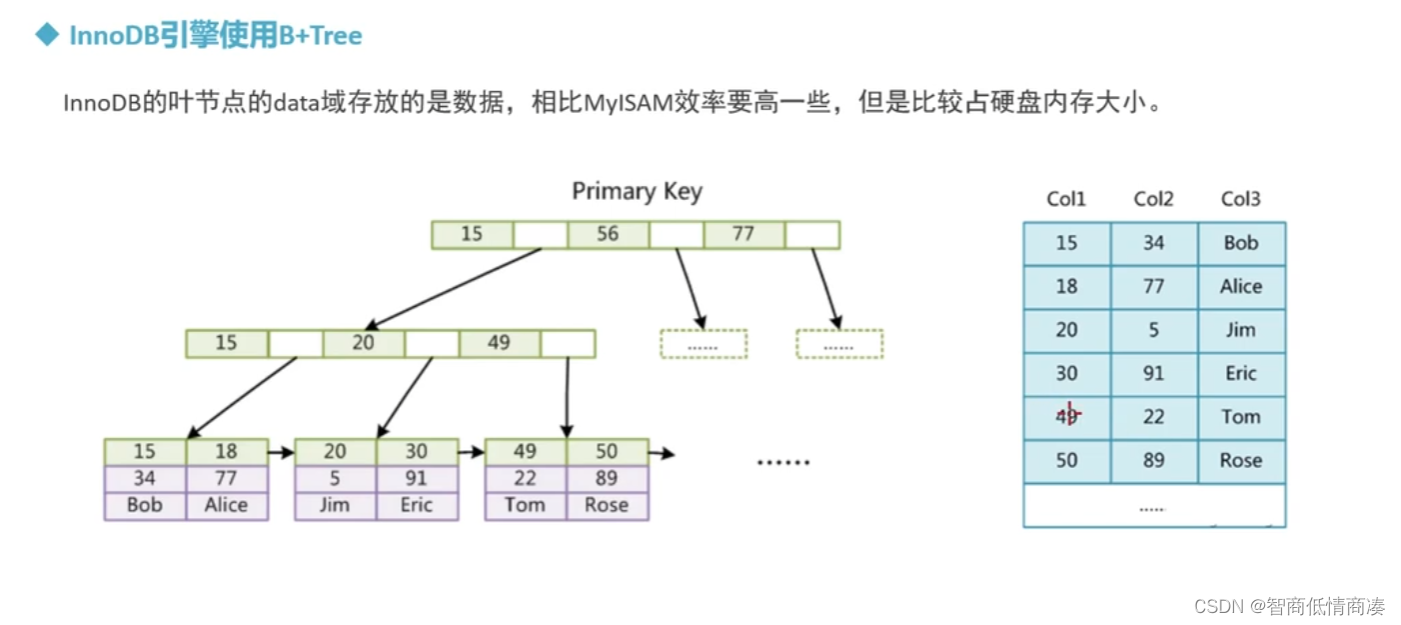
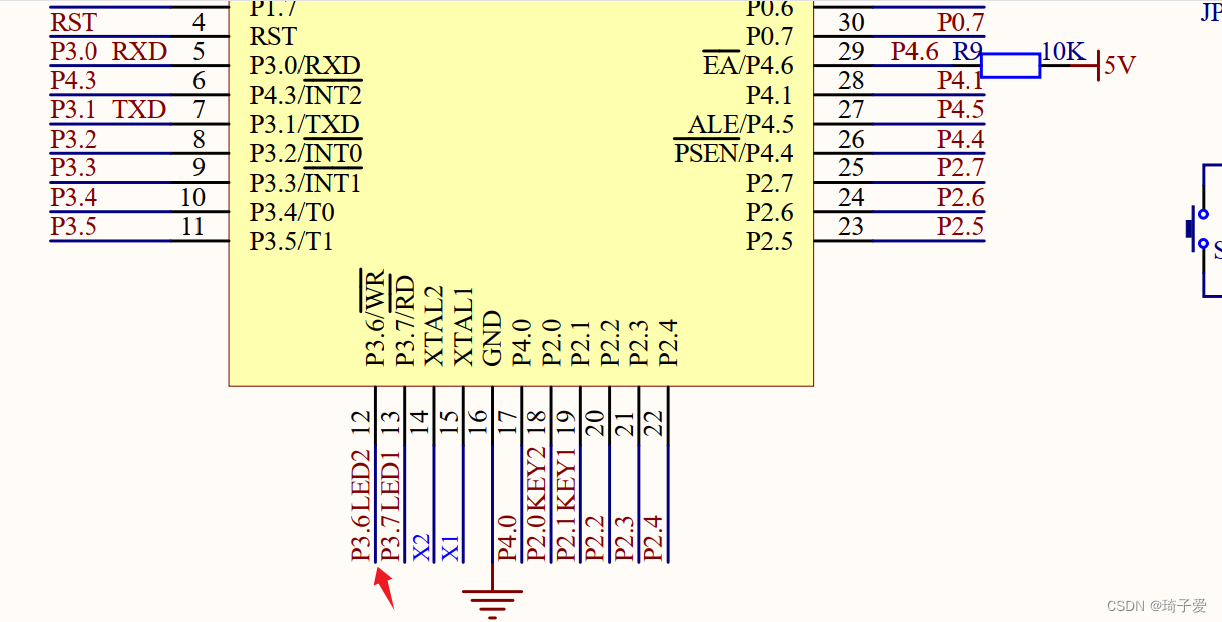
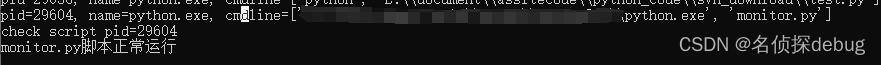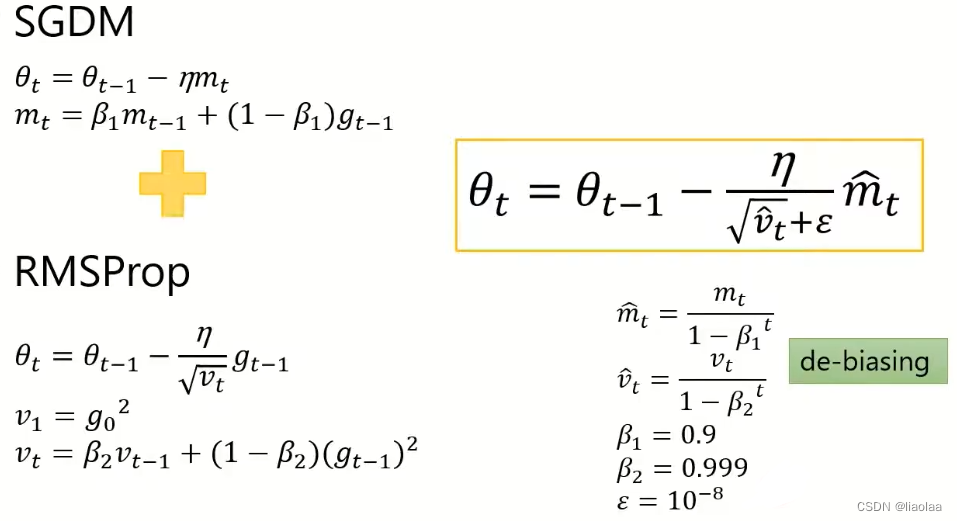思路：

1. 经验+题目要求
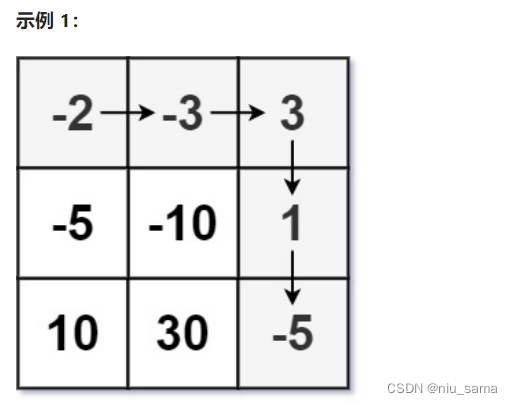
   a.以某个位置为结尾…
   dp[i][j]表示：走到【i，j】位置的时候，所需要的最初最低血量。
   b.以某个位置为起点
   dp[i][j]表示，从【i，j】出发，到达终点，所需要的最低初始健康血量

对于a思路来讲，我们需要上一步的两个位置的状态来更新下一个状态，就拿示例1来举例：我们要想从-2走出去，就需要3血量，但是无论走到下一步-3还是-5都会死，所以我们还会受到下两步的影响，所以这个思路不行。

对于b思路，倒着来的，
我们从-5走到终点，所需最小为6，
然后从1走向-5，我们要让所需的最小血量变为也就是6-1，为5，
然后从3走向1，变为5-3，为2，
然后从-3走向3，变为2-(-3)为2，为5；
然后从-2走向-3，变为5-(-2)即为7.

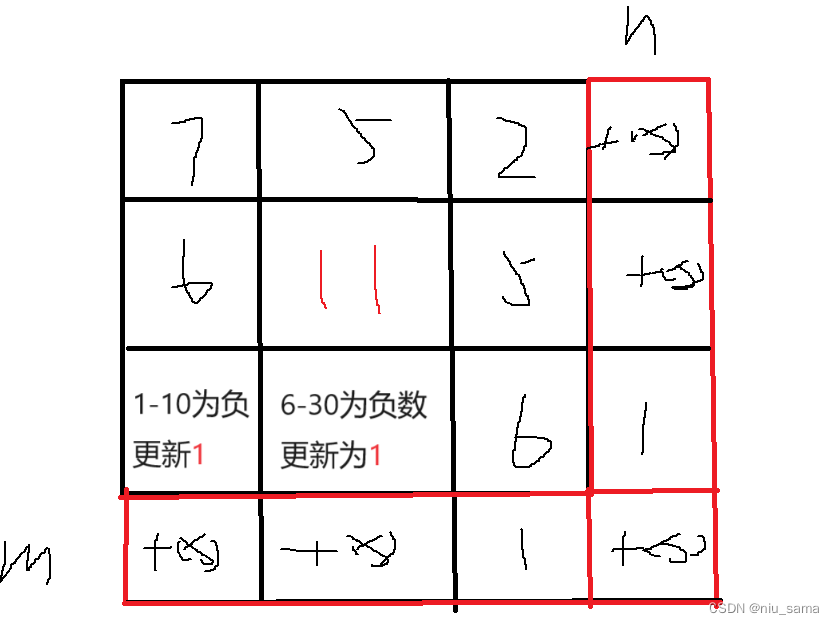
2.在三角符号处，我们假设所需走到终点所需最小血量为x，就有x + d[i]j >= dp[i]j+1； 就有x >= dp[i][j+1] - d[i][j]
但是，又不能让血量为0或负数，所以每个dp[i][j]都需要取max(1,dp[i][j]), 如果为负数就更新为1

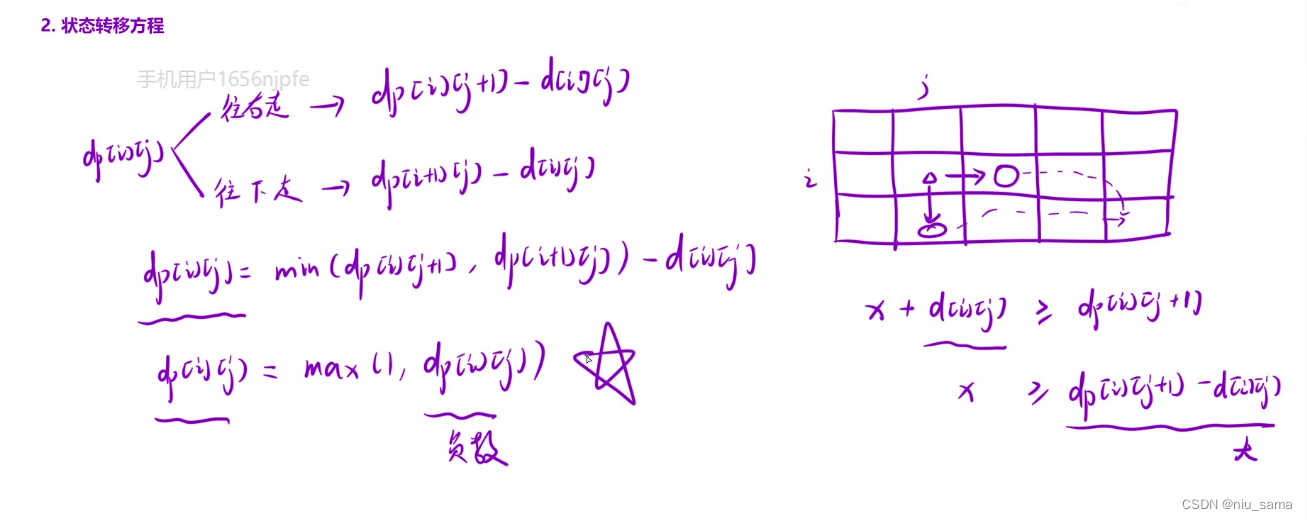
3.注意，有i+1，j+1，多加一行一列，但是加在右下。
最右下角的那个值要想正确，就取决于箭头指向那个两个位置的值，而且想要活着出去，剩的值最少是1。其他值都不影响结果就行。

4.从上到下填写每一行，每一行从左向右。

class Solution {
public:
    int calculateMinimumHP(vector<vector<int>>& dungeon) {
        int m = dungeon.size();
        int n = dungeon[0].size();
        vector<vector<int>> dp(m+1,vector<int>(n+1,INT_MAX));//建表并初次初始化
        dp[m][n-1] = dp[m-1][n] = 1;//初始化
        for(int i = m-1; i>=0; i--)//填表
        {
            for(int j = n-1; j>=0; j--)
            {
                dp[i][j] = min(dp[i+1][j],dp[i][j+1]) - dungeon[i][j];
                if(dp[i][j] <= 0)//血量为负数就更新
                    dp[i][j] = 1;
            }
        }

        return dp[0][0];

    }
};

对应的示例图：