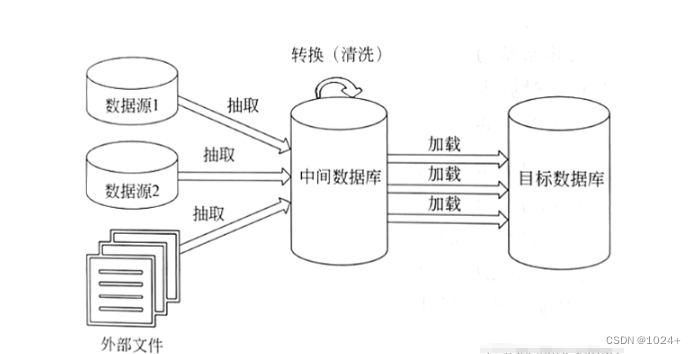
矩阵，一个令人头疼的名字，学过线性代数的友友们想必对矩阵的运算规则烂熟于心，与它延申出来的向量知识曾经让我们深陷其中。矩阵在高级的数据存储中占据着重要的地位。定义字典类型的过程，其实就是寻找key和value关系的过程，定义list的过程，其实就是存储各类数据的过程，而定义矩阵的过程，和list有点关系，我们看成是将list方向化。今天我们看看，GEE上，如何对矩阵进行一系列操作。
1.定义矩阵数据
//定义一个二维数组
var array1 = ee.Array([[1,2,3,4,5,6],
[2,3,4,5,6,7],
[3,4,5,6,7,8],
[4,5,6,7,8,9],
[5,6,7,8,9,10],
[6,7,8,9,10,11]]);
print("Array1:",array1);为了方便大家理解代码，小编多敲了几个换行，此处定义了一个6*6的矩阵，通过ee.Array([[......],[......],.....])进行矩阵的定义。如果小编要定义2*4的矩阵或者是4*2的矩阵，应该如果写参数？
var A1 = ee.Array([[1,2,3,4],[2,3,4,5]]);//2*4
var A2 = ee.Array([[1,2],[2,3],[3,4],[4,5]]);//4*2
print("2*4:",A1,"4*2",A2);结果如下：
2.创建单位矩阵
//创建单位矩阵
var arrayId = ee.Array.identity(6);
print("arrayId:",arrayId);单位矩阵在是矩阵的基本单元，支撑了矩阵的多种运算技巧。在GEE上通过使用：
ee.Array.identity(number)
可以创建number*number规格的单位矩阵，此处小编创建了6*6的单位矩阵。结果如下：
3.创建重复矩阵
//创建重复矩阵
var arrayRe0 = ee.Array([[1,2,3],
[2,3,4]]).repeat(0,2);
var arrayRe1 = ee.Array([[1,2,3]
,[2,3,4]]).repeat(1,2);
print("arrayRe0:",arrayRe0,"arrayRe1",arrayRe1);创建重复矩阵可以将同一行或者是同一列进行复制，使用：
ee.Array.repeat(axis,count)
即按照指定的坐标轴进行矩阵内容的复制，这里的轴包括0轴和1轴，其中0轴代表行轴，1轴代表列轴，count指的是要复制的次数。此处小编首先想围绕给定的0轴按行进行复制2次，其次，小编想通过按列轴的形式，对矩阵的两列复制两次，最后得到的结果如下：
4.矩阵的四则运算
//进行加减乘除四则运算
var array2 = ee.Array([[1,2],
[2,3]]);
var array3 = ee.Array([[2,4],
[4,6]]);
print("add:",array2.add(array3));
print("subtract:",array2.subtract(array3));
print("divide:",array3.divide(array2));
print("multiply:",array2.multiply(array3));矩阵的四则运算比较简单，和Number数据类型的运算类似，分别采用add，subtract，divide，multiply即可完成相应的运算。
5.对矩阵的某一列或者某一行进行计算
//对某一行（0轴）或某一列(1轴）进行计算
var array4 = ee.Array([[1,2,3,4],
[4,3,4,5],
[3,4,5,6],
[8,5,6,7]]);
print("aXis 0:",array4.reduce(ee.Reducer.sum(),[0]));//传入0轴（行轴），计算每一列和
print("aXis 1:",array4.reduce(ee.Reducer.sum(),[1]));//传入1轴（列轴），计算每一行和此处小编定义了一个4*4的矩阵，合理运用：
ee.Array.reduce(Reducer,axls)
可以单独对矩阵的行和列进行计算，通过传入0轴，我们能够每一列的和，通过传入列轴，我们能够得到每一行的和。计算的结果如下：
6.矩阵的掩膜
//矩阵的掩膜
var array5 = ee.Array([[1,1,1],
[2,3,4],
[5,6,7],
[1,1,1]]);
var array6 = ee.Array([[1],
[0],
[1],
[0]]);
print("array5:",array5,"array6",array6);
print("Mask:",array5.mask(array6));掩膜的作用是保留想要的矩阵的部分，此处下边定义了一个4*3的矩阵，想保留第一行和第三行的数据，因此在掩膜矩阵定义的4*1矩阵中，将第一行和第三行设置为1，第二行和第四行设置为0，这样便能够保留第一行和第三行的数据了。其他行或列的保留大家可以模仿试试看。
7.矩阵的转置
//矩阵的转置
var array7 = ee.Array([[1,1,1],
[2,3,4],
[5,6,7],
[1,1,1]]);
print("array7:",array7);
print("transpose:",array7.transpose());矩阵的转置即原行变新列，原列变新行的过程，它和原矩阵之间存在微妙的关系，我们在线代中已经学过。在GEE中使用：
ee.Array.transpose()
可以实现矩阵的转置，得到的结果如下：
8.矩阵内元素格式的转换
//矩阵内元素的数据格式转换
var array8 = ee.Array([[1.3,4.5,6.8],
[5.27,4.22,6.08]]);
print("array8:",array8);
var transform = array8.uint8();
print("Transfrom:",transform);遇见小数的矩阵，总想转为正数，使用：
ee.Array.uint8
即可按照四舍五入的原则进行数据的转换，除此之外，还有很多数据类型的转换方法，大家可以查阅GEE上封装的相关方法，用起来都差不多，篇幅原因，就不一一介绍啦！
9.矩阵的交并运算
//矩阵的交并操作
var array11 = ee.Array([[2,0,2],
[0,1,3],
[4,2,0]]);
var array12 = ee.Array([[3,1,0],
[1,1,2],
[0,1,0]]);
print("Array11:",array11,"Array12:",array12);
print("ArrayAnd:",array11.and(array12));
print("ArrayOr:",array11.or(array12));交并我们在在前面的数据集中已经聊过，最后返回的数据比较简单，就是0和1，and和or也是常见的方法，这里就只展示结果哈！
10.矩阵的比较
//矩阵的比较方法，对应元素比较，得0或1；
var array9 = ee.Array([[1,2,3,4],
[4,3,4,5],
[3,4,5,6],
[8,5,6,7]]);
var array10 = ee.Array([[1,2,5,6],
[4,5,8,1],
[2,4,6,6],
[8,5,6,9]]);
print("array9:",array9,"array10",array10);
var compare = array9.eq(array10);
print("Compare:",compare);矩阵的比较主要是判断两个矩阵是否相等，通过对应元素一一eq，返回1或0来确定，1代表两个矩阵的对应元素相等，0代表两个矩阵的元素不同。此处小编定义两个矩阵进行判断，得到的结果如下所示：
关于GEE的矩阵的基本操作到这里就结束了，如果对你学习有帮助，不要忘记了给小编点赞哦！更多内容，欢迎关注小编的公众号“梧桐凉月”，谢谢大家！
本期代码链接：
https://code.earthengine.google.com/d43d5b7e413d72121fdc35ab00b6690d
https://code.earthengine.google.com/d43d5b7e413d72121fdc35ab00b6690d
![[word] 怎么把word表格里的字放在正中间？ #职场发展#知识分享#知识分享](https://img-blog.csdnimg.cn/img_convert/f35c948dbf16018bd09033216ad272a6.jpeg)
