做题步骤:
-
确定dp数组的含义(一维或者二维)
-
获取递推公式
-
dp数组如何初始化
-
确定遍历顺序
-
打印dp数组(检查)
题目:
1. 斐波那契数 509
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
解析:
-
dp数组为存放斐波那契数的容器,下标 i 代表存储斐波那契数值n的位置。
-
递推公式:
dp[i] = dp[i - 1] + dp[i - 2]
-
遍历顺序从前向后
所以解题代码如下:
class Solution {
public int fib(int n) {
if(n < 2){
return n;
}
int[] dp = new int[n + 1];
dp[0] = 0;
dp[1] = 1;
for(int i = 2; i <= n; i++){
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
}2. 爬楼梯 70
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
解析:
-
dp数组为存储爬楼梯方法数的容器,即爬到第 dp[i] 阶有 i 种方法。
-
递推公式:
dp[i] = dp[i - 1] + dp[i - 2]
-
由于dp[0]是无意义的,同时题目要求
1 <= n <= 45所以我们从1开始初始化即:d[1] = 1, d[2] = 2 -
遍历顺序从前向后
所以解题代码如下:
class Solution {
public int climbStairs(int n) {
if ( n == 1) return 1;
int[] dp = new int[n + 1];
dp[1] = 1;
dp[2] = 2;
for(int i = 3; i <= n; i++){
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
}3. 使用最小花费爬楼梯 746
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
解析:
-
dp数组为存储该层向上跳跃所花费能量的容器。i 表示层数。
-
递推公式:
-
由于到达 i 层存在两种方式
-
通过 i - 1跳一步,花费能量:
dp[i] = dp[i - 1] + cost[i - 1];
-
通过 i - 2 跳两步,花费能量:
dp[i] = dp[i - 2] + cost[i - 2];
-
所以综上所述我们的递推公式为:
dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
-
-
接下来初始化由于题目给出我们可以在0或1位置起跳,所以
dp[0] = dp[1] = 0
-
遍历顺序为从前向后
所以解题代码如下:
class Solution {
public int minCostClimbingStairs(int[] cost) {
int[] dp = new int[cost.length + 1];
dp[0] = 0;
dp[1] = 0;
for(int i = 2; i <= cost.length; i++){
dp[i] = Math.min((dp[i-1] + cost[i-1]),(dp[i-2] + cost[i-2]));
}
return dp[cost.length];
}
}4. 不同路径 62
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
解析:
-
dp数组表示一个存储到达当前位置的路径方法数目的容器。
-
递推公式:
-
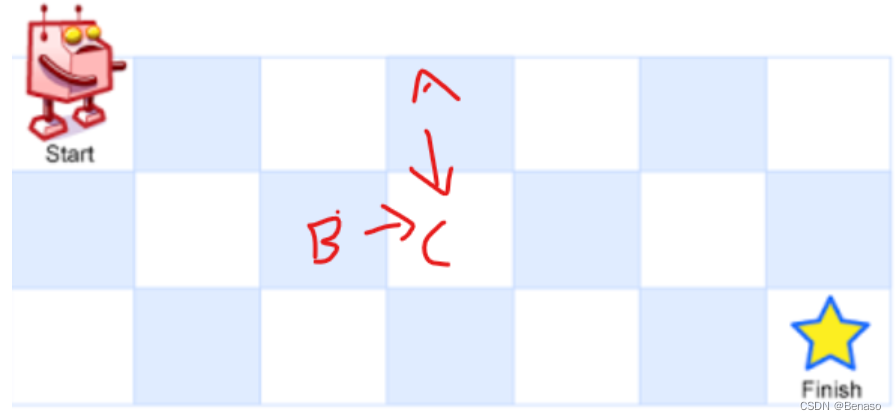
比如我们的dp[i][j]是 C 这个位置的路径数目,我们到达 A 的路径数目有 dp[i - 1][j] 种,我们到达 B 的路径数目有 dp[i][j - 1] 种。由于机器人只能向左或者向右行走,所以我们的只能从 A 或者 B 到达 C 。所以 C 处路径总数为 A 处路径总数加上 B 处路径总数。
-
公式为:
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
-
初始化由于我们在出发点,到 x = 0 与 y = 0 位置的路径数都为1,即:

所以初始化 x = 0, 与 y = 0 即可:
for(int j = 0; j < n; j++) dp[0][j] = 1; for(int i = 0; i < m; i++) dp[i][0] = 1;
-
遍历方向为从上到下和从左往右
所以解题代码如下:
class Solution {
public int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
for(int j = 0; j < n; j++) dp[0][j] = 1;
for(int i = 0; i < m; i++) dp[i][0] = 1;
for(int i = 1; i < m; i++){
for(int j = 1; j < n; j++){
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
}5. 不同路径2 63
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
解析:
该题和上一题类似,递推公式一致,只需要额外增加以下两点:
-
递推公式需先判断该位置是否为0(无阻塞)
-
初始化时,如若在 x = 0 或 y = 0 位置遇到阻碍则阻碍之后的dp数组初始化定义为 0 (或null):
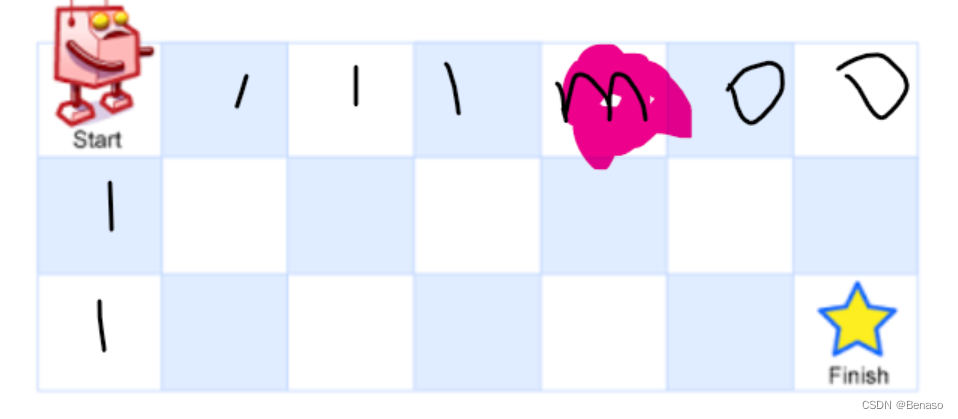
所以解题代码如下:
class Solution {
public int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
for(int j = 0; j < n; j++) dp[0][j] = 1;
for(int i = 0; i < m; i++) dp[i][0] = 1;
for(int i = 1; i < m; i++){
for(int j = 1; j < n; j++){
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
}6. 整数拆分 343
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
解析:
-
dp数组含义:i表示正整数值, dp[i]表示乘积最大值。
-
递归公式:
-
由于dp[i] = j * (i - j) => dp[i] = j * dp[i - j] (即在原有基础上在进行一次拆分);
-
由于我们去最大值,所以为
Math.max(Math.max(j * (i - j), j * dp[i-j]), dp[i])
注解:为什么要再一次比较 dp[i] 呢?
答:由于我们在遍历时,每次 j++ , dp[i]都保存上一次的最大值,所以我们需要比较当前最大值和历史最大值,取其中大的为返回值。
-
-
初始化 dp[0] = 0, dp[1] = 0, dp[2] = 1;
-
遍历方向:从左至右
所以解题代码如下:
class Solution {
public int integerBreak(int n) {
int[] dp = new int[n + 1];
dp[0] = 0;
dp[1] = 0;
dp[2] = 1;
for(int i = 3; i <= n; i++){
for(int j = 1; j <= i - j; j++){
dp[i] = Math.max(Math.max(j * (i - j), j * dp[i-j]), dp[i]);
}
}
return dp[n];
}
}