Push-Relabel算法相关阅读
- 1.Push-Relabel算法思想
- 2.Push-Relabel算法原理示意图
- 3.Push-Relabel算法具体实例
- 4. 网络流各类算法简单总结与比较
- 5. Push-Relabel 预流推进算法
- 6. Push-Relabel算法(最大流)
1.Push-Relabel算法思想
对于一个网络流图: 该算法直观可以这样理解,先在源节点处加入充足的流(跟源节点ss相连的所有边的容量之和),然后开始按一定规则进行流渗透,一个边一个边的向汇点渗透,直到没法再渗透(类似于Ford-Fulkerson算法中找不到增广路径了),那么这时再把一些剩余的流回收到源节点ss就可。
主要分为两个步骤:push和relabel。push表示从所有节点找出一个存水量大于0的节点uu,将它所存的水尽可能推向与它相邻的节点vv。要实现该push的操作必须满足下面条件:该点存水量e(u)>0e(u)>0,节点uu的高度大于节vv的高度。本次推送的流值(u,v).f=mine(u),(u,v).capacity(u,v).f=mine(u),(u,v).capacity,(u,v).capacity(u,v).capacity为边 edge(u,v)edge(u,v)的当前容量,这个值在推进过程中会一直变换。relabel表示某一个节点存水量大于0但水流不出去时,我们对该节点高度增加1,这就是所谓relabel操作,使得该节点的存水量流入比它低的节点。一开始的时候我们设置源节点高度为N,此处N为节点数N,此处N为节点数,其他所有节点高度为0,并且汇节点的高度固定为0,其他节点高度在算法执行过程中高度hh会改变。
算法步骤:
1.初始化前置流:将与源点s相连的管道流量f(0,i)设为该管道的容量,即 f(0,i)=c(0,i);将源点s的高度h(0)=V,(V表示图的顶点个数),其余顶点高度h(i)=0;将源的点余量e(0)设为源容量减去源的流出量,即e(0)=-∑f(0,i)=-∑c(0,i),与源s相连的点余量设为该点的流入量e(i)=c(0,i),其余点都为0。
2.搜索是否有节点的点余量e(u)>0e(u)>0,如果存在,表示要对该点进行操作——重标记或者压入流:检查与该点u全部的相邻点v,若该点比它相邻点的高度大h(u)>h(v),该管道的当前容量为c(u,v)c(u,v),将该点u的余量以最大方式压入该管道delta=min(e(u),c(u,v))delta=min(e(u),c(u,v)), 然后对节点u,v的余量e、边(u,v)的容量进行相应的进行减加操作;如果找不到高度比自己低的相邻节点v,则对节点u的高度增加1,即h(u)=h(u)+1h(u)=h(u)+1。如此继续进行Push操作。以上的重标记或压入流操作循环进行,直至该点的余量e(u)为0。
3.重复第2步,直找不到余量大于0的节点,停止算法,最后输出汇点t的余量e(t), 该值就是最后所求的最大流。最小割。
2.Push-Relabel算法原理示意图
给定的网络流图如下:

第一步:初始化操作:
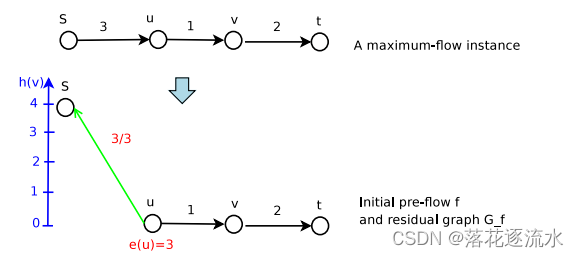
第一次Push不成功,进行Relabel
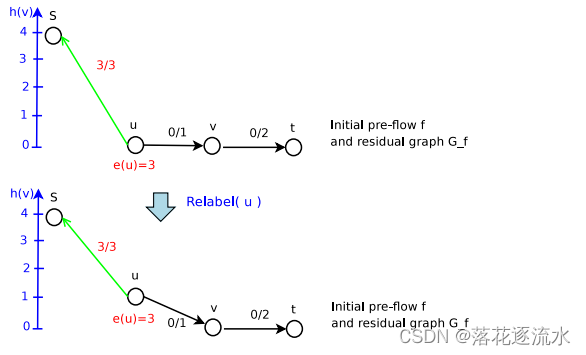
第二次Push,成功
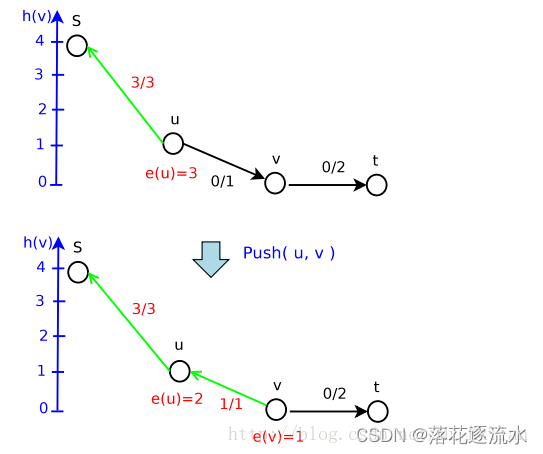
继续Push
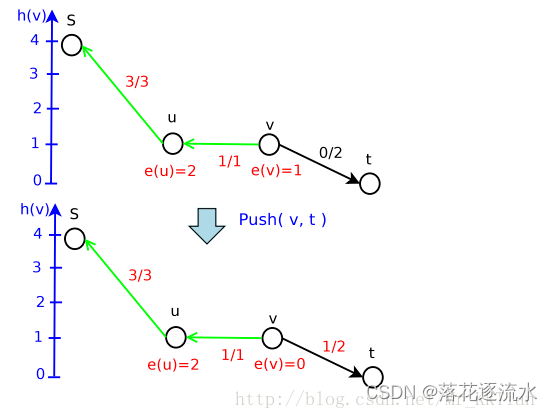
继续Push
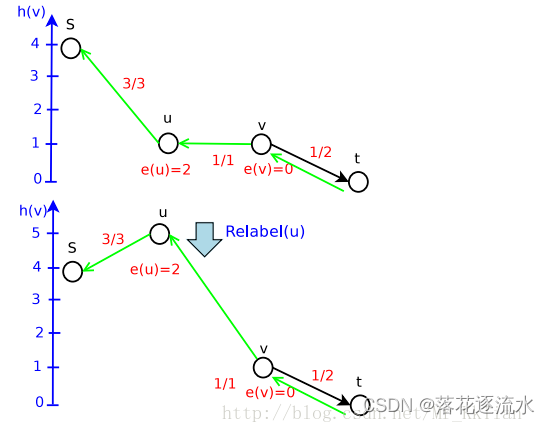
继续Push
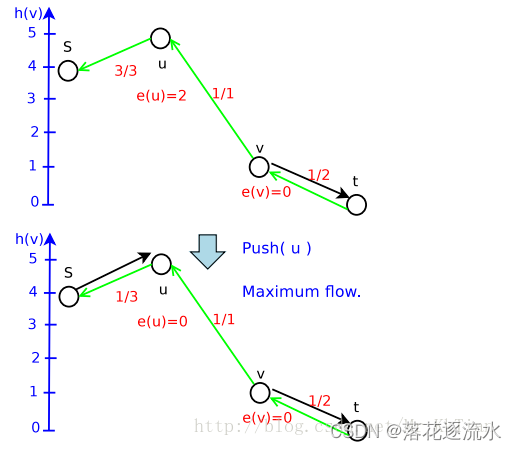
至此结束。
3.Push-Relabel算法具体实例
求解下面网络流图的最大流:
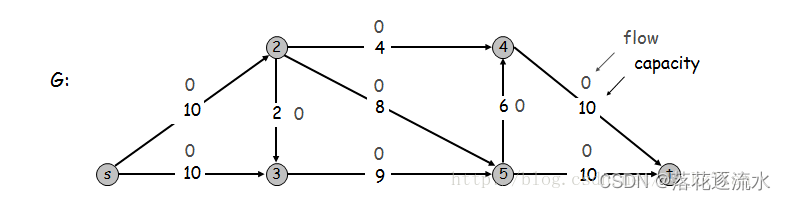
源节点为s,汇节点为t
具体程序实现如下:
/****************************************************
Description:Push-Relabel算法求解网络最大流
Author:Robert.TY
Date:2016.12.10
****************************************************/
#include<iostream>
#include<limits>
#include<iomanip>
using namespace std;
struct Point{
char ch;//节点标识
int e;//存货量
int h;//高度
};
Point point[6];
int graph[6][6]={{0,10,10,0,0,0},
{0,0,2,8,4,0},
{0,0,0,9,0,0},
{0,0,0,0,9,10},
{0,0,0,0,0,10},
{0,0,0,0,0,0}} ;
int Push_Relabel(int s, int t,int n); //参数为 起点 端点 节点数
int main(){
int n=6;
point[0].ch='s'; point[0].e=0; point[0].h=0;
point[1].ch='u'; point[1].e=0; point[1].h=0;
point[2].ch='v'; point[2].e=0; point[2].h=0;
point[3].ch='a'; point[3].e=0; point[3].h=0;
point[4].ch='b'; point[4].e=0; point[4].h=0;
point[5].ch='t'; point[5].e=0; point[5].h=0;
cout<<"原始网络图邻接矩阵:"<<endl;
for(int i=0;i<=5;i++){
for(int j=0;j<=5;j++){
cout<<setw(6)<<graph[i][j]<<" ";
}cout<<endl;
}
cout<<"max_flow="<<Push_Relabel(0, n-1,n)<<endl;
cout<<"graph流图矩阵:"<<endl;
for(int i=0;i<=5;i++){
for(int j=0;j<=5;j++){
cout<<setw(6)<<graph[i][j]<<" ";
}cout<<endl;
}
return 0;
}
int Push_Relabel(int s, int t,int n)
{
int max_flow;
point[s].h = n; //起始点高度置为n 最高
//初始化 将start点的库存 流出去 update剩余图
for (int u = 1; u <= t; u++) {
if (graph[s][u] > 0) {
point[u].e = graph[s][u];
point[s].e -= graph[s][u];
graph[u][s] = graph[s][u];
graph[s][u] = 0;
}
}
while(1) {
int finishflag = 1;
for (int u = s+1; u < t; u++) { //搜索除 节点s 节点t以外的节点
if (point[u].e > 0) { //发现库存量大于0的节点 u 进行push
finishflag = 0;
int relabel = 1; //先假设顶点u需要relabel 提高高度h
for (int v = s; v <= t && point[u].e > 0; v++) { //搜索能push的顶点
if (graph[u][v] > 0 && point[u].h >point[v].h) { //发现节点v
relabel = 0; //顶点u不需要relabel
int bottleneck = min(graph[u][v], point[u].e);
point[u].e -= bottleneck; //u节点库存量减少
point[v].e += bottleneck; //v节点库存量减少
graph[u][v] -= bottleneck;
graph[v][u] += bottleneck;
}
}
if (relabel==1) { //没有可以push的顶点,u节点需要relabel 提高高度
point[u].h += 1;
}
}
}
if (finishflag==1) { // 除源点和汇点外,每个顶点的e[i]都为0
max_flow = 0;
for (int u = s; u <= t; u++) {
if (graph[t][u] > 0) {
max_flow += graph[t][u];
}
}
//cout<<"max_flow="<<max_flow<<endl;
break;
}
}
return max_flow;
}
结果如下:
原始网络图邻接矩阵:
0 10 10 0 0 0
0 0 2 8 4 0
0 0 0 9 0 0
0 0 0 0 9 10
0 0 0 0 0 10
0 0 0 0 0 0
max_flow=19
graph流图矩阵:
0 0 1 0 0 0
10 0 2 2 0 0
9 0 0 0 0 0
0 6 9 0 4 0
0 4 0 5 0 1
0 0 0 10 9 0
--------------------------------
Process exited after 0.0801 seconds with return value 0
Press ANY key to exit...
参考:最大流网络之Push-Relabel算法
4. 网络流各类算法简单总结与比较
容量,流量,可行流,残量网络等等基础概念不赘述了
第一类,增广路算法(Augmenting-Path):
该类算法是基于路径/割的,由Ford和Fulkerson两个人提出,实际上代表了一类算法,:
从零流开始考虑,假如有这么一条路,这条路从源点开始到达汇点,并且这条路上的每一段都满足Flow<C,
则我们一定能找到这条路上的每一段的C−Flow的值当中的最小值δ
把这条路上每一段的Flow都加上这个δ,一定是一个可行流,这样我们就得到了一个更大的可行流,而这条路就叫做增广路
我们不断地从起点开始寻找增广路,每次都对其进行增广,直到找不到增广路为止。当找不到增广路的时候,当前的流量就是最大流
这也是增广路类网络流的核心思路,下来就是这么找增广路,怎么增广了
(1)Dfs寻找任意一个增广路,并沿着路进行增广复杂度为O(E|Maxflow|)这个算法一般认为这个是Ford-Fulkerson算法
实际上一般认为的FF算法是不寻找最短增广路也不划分层次图,每次只是对任意一个增广路去增广的算法.
(2)Edmonds-Karp/SAP/最短增广路算法 利用BFS寻找最短增广路径,
由于存图方式的不同,邻接表O(VE2),邻接矩阵O(V3)
(3)MPLA/最短路径增值算法 在残量网络上引入层次,
构建层次图O(V),V个阶段每个阶段多次BFS寻找增广路O(E2),总复杂度上界为O(VE2)
(4)Dinic/Blocking Flow Algorithm/阻塞流算法 用一次DFS代替MPLA的多次BFS增广
同样建立层次图O(V),V个阶段,每个阶段一次DFS寻找增光路O(VE),总复杂度上界为O(V2E).
(5)ISAP,一般认为是加入了GAP优化的SAP算法,时间效率和 Dinic差不多,可以说为 EK算法的优化版。时间复杂度O(V2E)
(6) Capacity-Scaling/ScalingFord-Fulkerson/Bit-Scaling/容量缩放算法,
把容量视作二进位数字,从最高位开始,每回合添加一个位数,扩充流量,寻找增广路,填满多出的容量,达到最大流。
显然,当使用邻接矩阵时,复杂度O(E2log(Cmax)V2),使用邻接表时是O((V+E)Elog(Cmax))Cmax$为边上的最大容量
第二类,预流推进类算法
该类算法是以点为基础的
1.推进/push:
我们认为汇点是最低点,源点是最高的,推进模拟水流在图上流动到汇点的过程,我们每次先把水流流入中间节点,再逐步向后推进
2.储流,过载/excess/overflowing:
为了实现推进,我们给每个点一个储流量,点就可以分为储流点/非储流点,储流点(也叫过载点),为了下一步的推进保存当前流量,
显然,对于任意一个点,实际上的流入==流出,换句话说,除了汇点和源点,所有点应该是不储流的,但显然目前是"过载"/overflowing的
3.可行边/admissible edge与高度标号/height label:
给每个点进行高度标号,并规定只能从高点向地点流量,与层次图类似
4.预流/preflow:
由于每次只到下一层推进,所以预先推进源点的流量到所有相邻点中
5.重标号/relabel:
当一个点无法流动,就抬高它,让水可以回流/流到同高度的点上
6.重回/retreat:
可以想见的是,所有中间节点都无法继续流下去,显然根据重标号,中间节点会愈来愈高,甚至高于源点,当所有的过载流量终将沿着反向边回流到源点,至此算法结束
实际过程中的基本框架就是对图上各点不断推进和重标号,直到无法进行为止,或者说,最大流存入汇点,多余的流量流回起点,所有其他点均不储流/不过载
最终汇点的储流量/源点所流出的流量,就是最大流。
下来就是怎么推进,怎么重标号了
1.朴素预流推进算法/Push-relabel algorithm with FIFO:
每个点重标号次数 O(V) 一共 O(V2) ,邻接矩阵每推一次为 O(V) 邻接表 为常数
标号一共O(V3) 或 O(EV2)
每个边可能被推进O(V)饱和情况下一共O(VE)非饱和情况下一共O(EV2)
用一个队列保存储流点即可.
2.重标优先预流推进/Relabel-to-front Algorithm
建立链表,保存当前图的拓扑序形式,不含源点汇点,按照拓扑序取点,跳过非储流点,把之前被推进过的点重新放入表头,并推进
3.最高标号预流推进/Highest-Label Preflow-Push Algorithm/HLPP
使用优先队列,每次取出最高标号点进行推进,直到结束,理论复杂度
O
(
s
q
r
t
(
m
)
n
2
)
O(sqrt(m)n^2)
O(sqrt(m)n2)可以使用GAP优化!
其实也可以发现,高度标号和层次图有异曲同工之妙
最后 给一个权威表格,甚至引入了动态树,不过没有HLPP算法
https://www.cnblogs.com/nervendnig/p/8927015.html
| Method | Complexity | Description |
|---|---|---|
| Linear programming | Constraints given by the definition of a legal flow. See the linear program here. | |
感想…
但实际上目前竞赛中常用的算法,无论是Dinic还是ISAP或是HLPP,他们的速度都无法与单纯的最短路算法相比,就连理论上界达到O(VE)最高的SPFA都无法达到
而目前科学界理论下界最低的,是Orlin’s提出的集大成者,复杂度上界达到O(VE),但是目前还没有进入算法竞赛中来,目前所有的网络流题目复杂度都是按照O(V2E)来的
但是,实际上无论是网络流还是费用流,我们目前均不需要复杂度如此低的算法
绝大多数模型都不会需要建立一个极端的稠密图/链形图,点数和边数经常是处于一个数量级的,对于O(EV2)的算法足够用了
研究大量复杂度相近而实现方式不同的算法,在OI中是有意义的,
OI赛制中需要大量的不同数据来区分不同的人实力,达到区分度,这也是OI选手对于复杂度,读入输出,花式优化的精益求精的原因,
以Bellmon-Ford最短路为例,的复杂度达到了O(VE)
但是实际上有队列优化,不重复入队/重复入队,SLF,均值,转DFS,邻接表指针化等等不同的优化/实现方式
在不同的图中都有不同的效果,即使其理论复杂度依然是O(VE),但只要选手根据不同的图去选择优化方式,就几乎无法被卡了
而且对于一个题,即使你的复杂度无法满足数据量,你依然可以通过其中很多的数据组,得到很多分,此时,一个优化到极致的算法就很重要了…
而在ICPC赛制中,区分度更多的在题目本身的思维,程序准确性,与复杂度上界,因为所有算法都通过所有的样例,也就是说必须用正确的复杂度通过,
在这种情况下,错误的复杂度毫无意义,必须选择一个复杂度稳定,编码容易,灵活的稳定算法,且从下手的一开始,就必须尝试去满足所有的极限数据和情形
OI的90分可以接受,而ICPC90分就是0分,且0ms的AC和10000ms的AC都同样正确,尤其对于网络流,建一个正确合适网络图,比花式优化的效果更大,尤其是减少多余边
总结,最大流的推荐算法有三个,且代码量均不长,资料也可以找到,:
1.Dinic 最常见的算法,可以加上各种优化方法,但无法改变理论上界
2.ISAP 依然是常见的算法,依然可以加上各种优化方法,据说是实践中最快的
3.HLPP 常见(?)算法中理论上界最低的一个,而且也可以加入不少优化,但可以参考的代码较少,尽管这个算法是最短的?
参考:网络流各类算法简单总结与比较
http://wiki.noip.space/graph/flow/max-flow/
5. Push-Relabel 预流推进算法
这个链接还有很多其他有价值的算法资源,值得细心看。
参考:http://wiki.noip.space/graph/flow/max-flow/
6. Push-Relabel算法(最大流)
Ford-Fulkerson方法还比较好理解,即每一次尝试都需要在剩余图里找到一条增强路径,让整个图的流量最大化。Push-Relabel算法与前面所讲的Ford-Fulkerson算法是另一种思路。
如果给你一个网络流,让你手算它的最大流,你会怎么算? 一般人都会尝试着从源点出发,让每条边的流量尽可能的大,然后一点点往汇点推,直到遇到一条比较窄的弧,原先的流量过不去了,这时再减少原来的量。其实这也是Push-Relabel算法的基本思路。
Push-Relabel算法,先在源节点处加入充足的流(与源节点相连的所有边的容量之和),然后按一定规则进行流渗透,一个边一个边的向汇点渗透,直到没法再渗透(类似于Ford-Fulkerson算法中找不到增广路径)。顾名思义,Push-Relabel算法包含两个核心的操作:
-
Push:Push操作表示从所有节点找出一个存水量大于0( e ( u ) > 0 e(u)>0 e(u)>0 )的节点 u u u ,将它所存的水尽可能推向与它相邻的节点 v v v 。要实现该push的操作必须满足下面条件:该点存水量 e ( u ) > 0 e(u)>0 e(u)>0 且节点 u u u 的高度大于节点 v v v 的高度。本次推送的流值 f = min { e ( u ) , c a p a c i t y ( u , v ) } f=\min\{e(u), capacity(u,v)\} f=min{e(u),capacity(u,v)} c a p a c i t y ( u , v ) capacity(u,v) capacity(u,v)为边 e d g e ( u , v ) edge(u,v) edge(u,v) 的当前容量。
-
Relabel:Relabel表示某一节点的存水量大于0( e ( u ) > 0 e(u)>0 e(u)>0),但水流不出去时,我们对该节点高度增加1,从而使得该节点的存水量流入比它低的节点。一开始的时候我们设置源节点( s s s )高度为 N N N ( N N N为 G G G 的结点数),所有其他节点高度为0,并且汇节点( t t t )的高度固定为0。除去 s$ 和 t t t 外,其他节点在算法执行过程中高度h会不断改变。
下面是简单的示例:
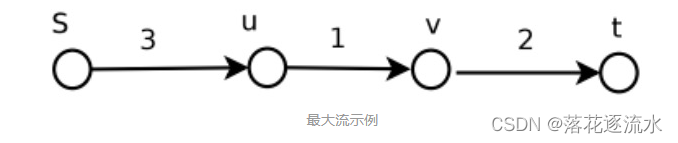

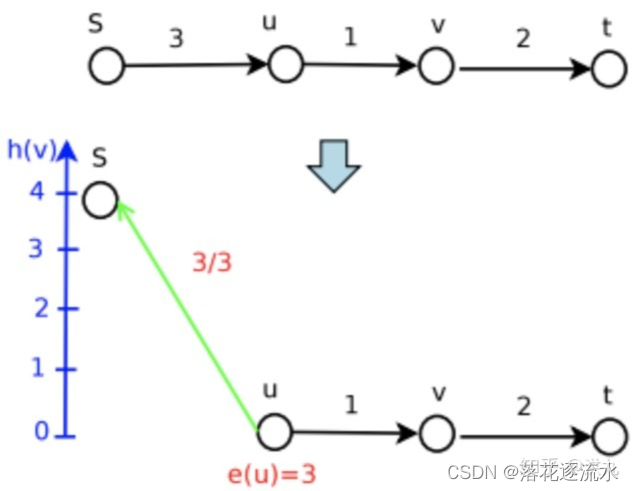
Step2:第一次Push不成功,进行Relabel (push不成功的原因是因为u的高度为0)
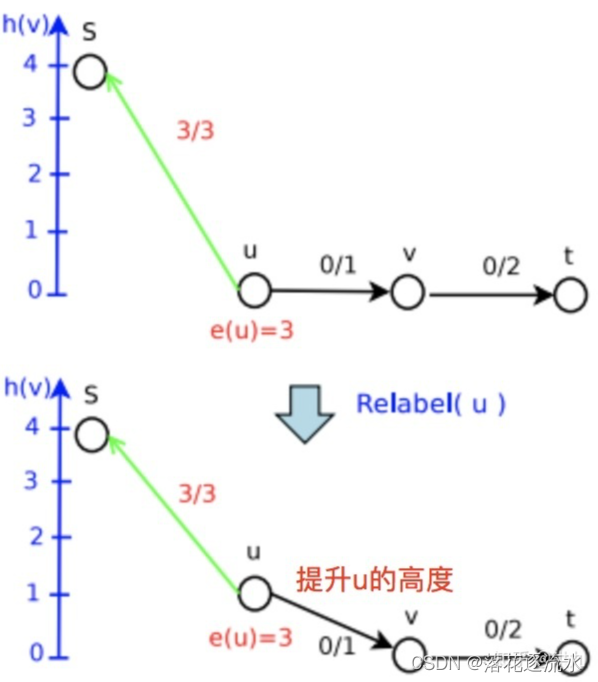
Step3:再次Push成功
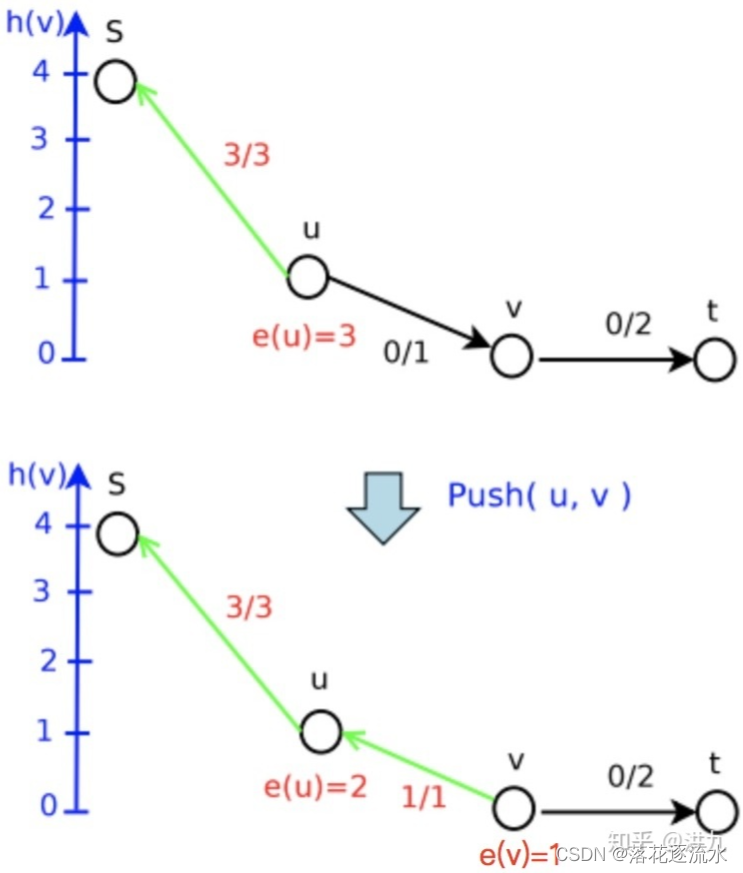
Step4:继续Push
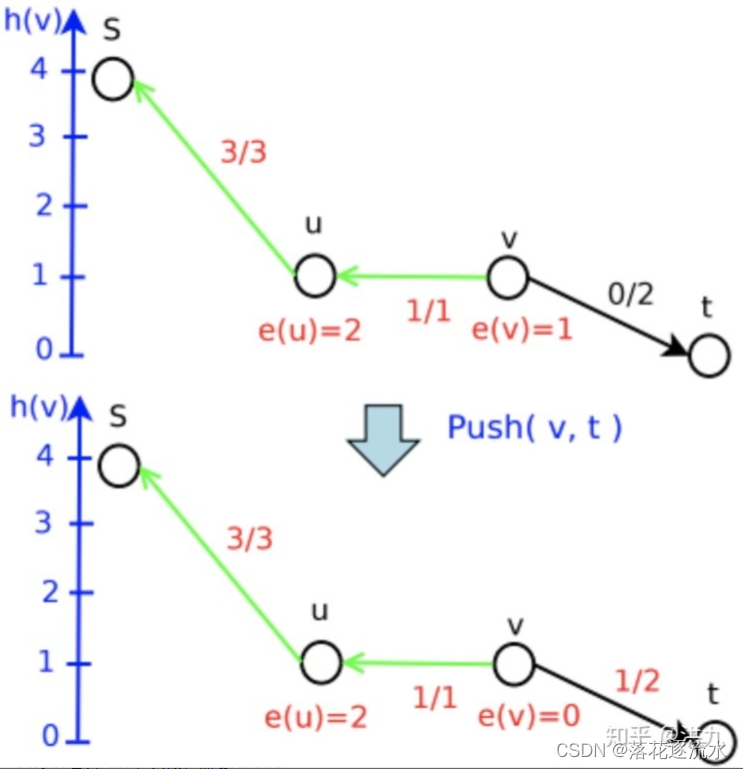
Step5:继续Push,失败,需要Relabel
当一个结点有盈余(
e
(
u
)
>
0
e(u)>0
e(u)>0),周围却没有高度比它低的结点的时候,我们就用Relabel重标号操作使它的标号上升到比周围最低的结点略高一点,使他的盈余能流出去。盈余不能困在某个节点里,对于任意一个非源非汇的结点,有盈余意味着它不满足流量平衡,也就意味着整个网络流不是一个真正合法的网络流。
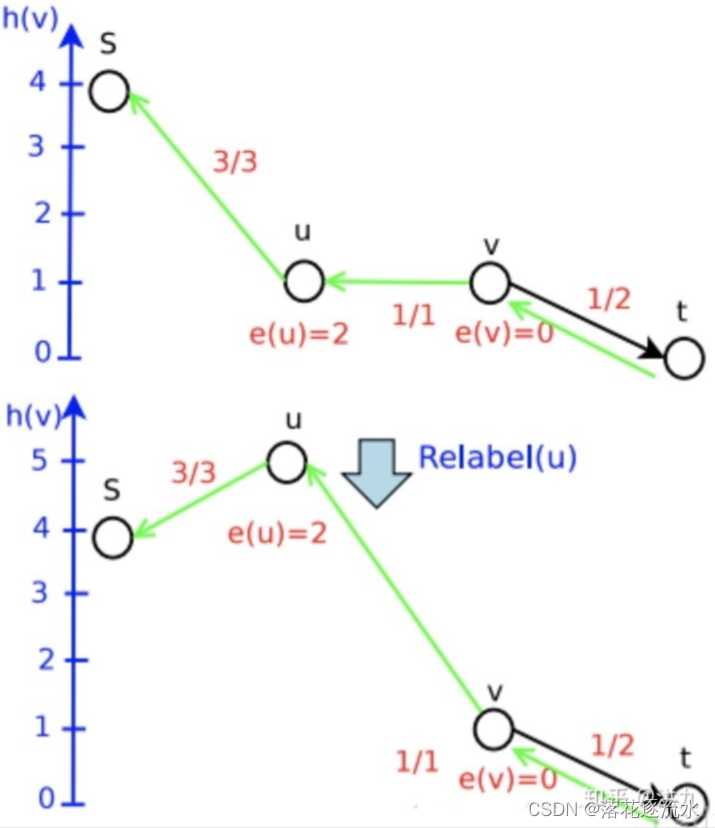
Step6.继续Push
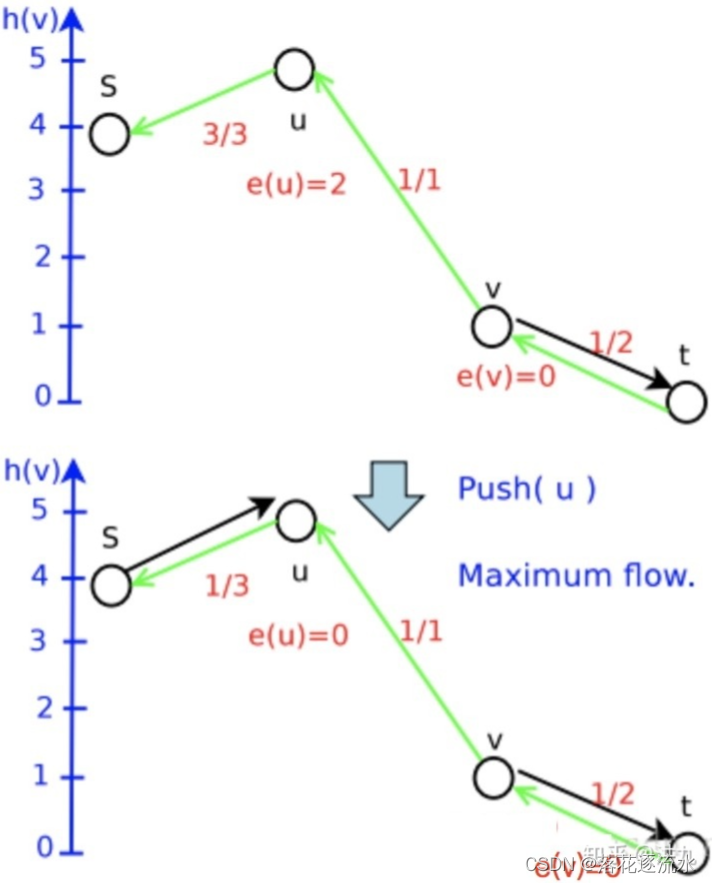
这一步是从
u
u
u 反向流向了
s
s
s 。相当于是从
s
s
s 多推出了一些流量到
u
u
u 再退还给
s
s
s 。这也正是后向弧(绿色线)的作用。程序是缺少大局观的,我们需要有一个能引导流的推进方向的机制,当它发现我们先前的推进是错误的时候,能沿着正确的后向弧推回来。
Step7:算法结束
直到找不到余量(
e
(
u
)
e(u)
e(u) )大于0的节点停止算法,此时网络达到了一种均衡状态,即所有结点的流入等于流出。最后输出汇点
t
t
t 的余量
e
(
t
)
e(t)
e(t) , 该值就是最后所求的最大流(最小割)。
Push-Relabel算法C代码如下:
#include <iostream>
#include <cstring>
using namespace std;
const int MAX_SIZE = 100;
const int INF = 1 << 30;
int capacityGraph[MAX_SIZE][MAX_SIZE];//即c[u][v]
int flowMap[MAX_SIZE][MAX_SIZE];//即f[u][v]
int height[MAX_SIZE];//高度h()
int excess[MAX_SIZE];//余流e()
int src, des;
int vertex_num, edge_num,account=0;//vertex_num顶点数,edge_num边数
// 初始设置
void init() {
memset(capacityGraph, 0, sizeof(capacityGraph));
memset(flowMap, 0, sizeof(flowMap));
memset(height , 0, sizeof(height));
memset(excess , 0, sizeof(excess));
cout<<"输入顶点数和边数:";
cin>>vertex_num>>edge_num;
cout<<"各边的数值:";
for( int i = 1; i <= edge_num; ++i ){
int start, end, cap;
cin>>start>>end>>cap;
capacityGraph[start][end] = cap;
}
src = 1;
des = vertex_num;
height[src] = vertex_num;
}
// 前置流
void preFlow() {
for( int i = src; i <= des; ++i ){
if( capacityGraph[src][i] > 0 ){
const int flow = capacityGraph[src][i];
flowMap[src][i] += flow;
flowMap[i][src] = - flowMap[src][i];
excess[src] -= flow;
excess[i] += flow;
}
}
}
// 压入
void push(int start,int end) {
int flow = excess[start]>(capacityGraph[start][end] - flowMap[start][end] )?(capacityGraph[start][end] - flowMap[start][end] ):excess[start];
flowMap[start][end] += flow;
flowMap[end][start] = -flowMap[start][end];
excess[start] -= flow;
excess[end] += flow;
}
// 重标记
bool reLabel(int index) {
int minestHeight = INF;
for( int i = src; i <= des; ++i ){
if( capacityGraph[index][i] - flowMap[index][i] > 0 ){
minestHeight = minestHeight> height[i]?height[i]:minestHeight;
}
}
if( minestHeight == INF ) return false;
height[index] = minestHeight + 1;
for( i = src; i <= des; ++i ){
if( excess[index] == 0 ) break;
if( height[i] == minestHeight && capacityGraph[index][i] > flowMap[index][i] ){
push( index, i );
}
}
return true;
}
void pushReLabel() {
bool flag = true;
preFlow();
while( true ){
if(flag == false) {
break;
}
flag = false;
for( int i = src; i <= des - 1; ++i ){
if( excess[i] > 0 ) flag = flag || reLabel( i );//此处每轮循环只执行一次函数reLabel( i ),当flag为TRUE时,不执行函数reLabel( i )
}
}
}
int main(){
init();
pushReLabel();
cout<<"max flow : "<<excess[des]<<endl;
return 0;
参考:策略算法工程师之路-图优化算法(二)(最小费用最大流求解)