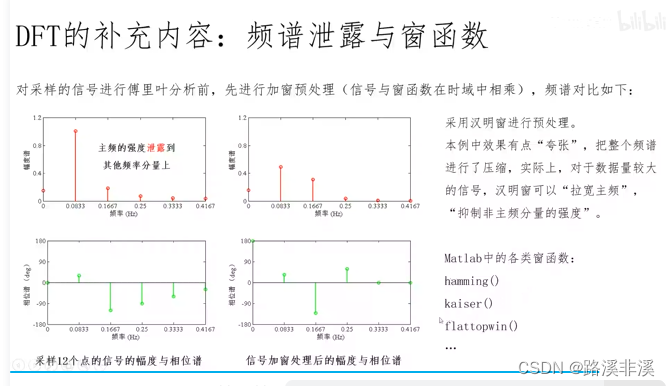
C++——STL之map和set
- 🏐序列式容器和关联式容器
- 🏀什么是键值对
- 🏐什么是set
- 🏀erase
- 🏀count
- 🏀lower_bound&&upper_bound
- 🏀equal_range
- 🏐multipleset
- 🏐什么是map
- 🏐multimap
- 🏐相关问题
- 🏀topk问题(前k个高频单词)
- 🏀两个数组的交集
- 💬总结
👀先看这里👈
😀作者:江不平
📖博客:江不平的博客
📕学如逆水行舟,不进则退
🎉欢迎关注🔎点赞👍收藏⭐️留言📝
❀本人水平有限,如果发现有错误的地方希望可以告诉我,共同进步👍
🏐序列式容器和关联式容器
C++ 容器大致分为 2 类,序列式容器和关联式容器。
- 序列式容器,其存储的都是 C++ 基本数据类型(诸如 int、double、float、string 等)或使用结构体自定义类型的元素。数据之间没有很强的关联性,就是挨着排。
- 关联式容器存储的元素,都是一个一个的“键值对”( <key,value> )。如果已知目标元素的键的值,则直接通过该键就可以找到目标元素,而无需再通过遍历整个容器的方式,具有很强的关联性。也是因为这个特性,数据的增删查改相比于序列式容器来说效率更高。
🏀什么是键值对
是一种具有一一对应关系的结构,这种结构有两个成员变量,一个是键值key,另一个是与key对应的value
在SGI-STL中关于键值对的定义:
template <class T1, class T2>
struct pair
{
typedef T1 first_type;
typedef T2 second_type;
T1 first;
T2 second;
pair() : first(T1()), second(T2())
{}
pair(const T1& a, const T2& b) : first(a), second(b)
{}
};
C++ STL 标准库提供了 4 种关联式容器,分别为 map、set、multimap、multiset。他们的底层结构都是红黑树,下面来看一下这些关联式容器吧。
🏐什么是set
以前学的一般都是两个参数,set是三个

可以看到这里给了一个Compare,和以前的学习优先级队列时的仿函数差不多,可以自己去写定规则去比较,比如T是自定义类型的时候,或者类如Date*这样的,自己需要去写一个比较规则,一个仿函数。
来看一下它的构造:
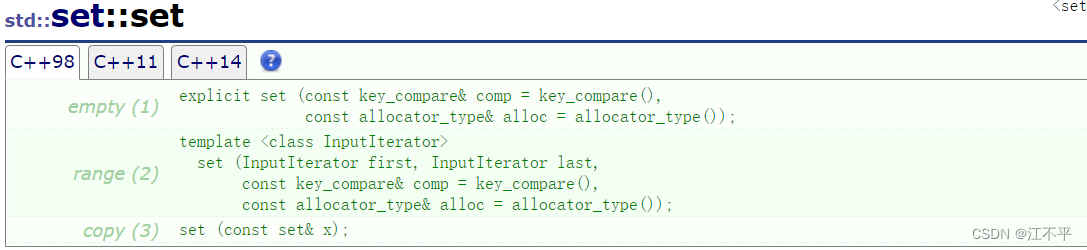
有一个全缺省构造,可以看到在构造这里也传这个仿函数进去,还有一个迭代区间构造,一个拷贝构造
这里拷贝构造是深拷贝,要拷贝一棵树,代价极大,所以如果不少特别需要,要谨慎拷贝
key模型支持增删查不支持改,因为本质是一棵搜索树,修改了就乱了。
void test_set()
{
/*set<int> s;
s.insert(4);
s.insert(2);
s.insert(1);*/
//我们还可以迭代器区间初始化,如果底层是连续的物理空间,那么原生指针就可以当作天然的迭代器
//当然还可以像下面这么写,list,vector都可以这么写,这是C++11里增加的列表初始化
/*set<int> s = { 3, 2, 1, 6, 3, 7, 5 };*/
我们可以用迭代器区间初始化如下面:
int a[] = { 3, 2, 1, 6, 3, 7, 5 };
set<int> s(a, a + sizeof(a) / sizeof(int));
这里set直接完成了排序和去重的功能,去重是间接作用出来的,因为这个地方3在第二次插入的时候发现前面插入过了,所以就没有继续插入。
// 排序 + 去重
set<int>::iterator it = s.begin();
while (it != s.end())
{
//*it = 10;
cout << *it << " ";
++it;
}
cout << endl;
for (auto e : s)//可以使用迭代器就可以使用范围for
{
cout << e << " ";
}
cout << endl;
如果说我们想实现降序的排序,我们怎么可以实现呢?第一种我们可以用反向迭代器,第二种我们可以直接去改变树,我们在初始化插入的时候,迭代器区间去初始化的时候我们这么写(用greater,但是在前面我们要加上#include< function > ):
set<int, greater<int>> s(a, a + sizeof(a) / sizeof(int));
我们可以看到迭代器在此处的作用,这是一种设计模式,它访问list,map,set,vector容器,没有暴露容器的底层结构,迭代器的优点在于不需要关心底层实现,这是一种封装的体现,你不需要去关心它是链表,顺序表还是说是树,用一种方式做到全都访问。
构造主要支持的核心方式是
那我们现在遍历它主要支持的核心方式是什么呢
🏀erase
erase往往与find分不开,那么下面这两种删除方式有区别吗?
s.erase(3);
for (auto e : s)
{
cout << e << " ";
}
cout << endl;
set<int>::iterator pos = s.find(3);
s.erase(pos);
for (auto e : s)
{
cout << e << " ";
}
cout << endl;
答:都是删除3的话在这个序列s上是没区别的。但是如果是下面这样就得出的效果就不一样了
s.erase(30);
for (auto e : s)
{
cout << e << " ";
}
cout << endl;
set<int>::iterator pos = s.find(30);
s.erase(pos);
for (auto e : s)
{
cout << e << " ";
}
cout << endl;
第一个呢,仍然不会报错,但是第二个用迭代器的会报错,这是什么原因呢,原来find在没有找到目标值时会返回end,所以删除出了问题。那么我们可以改进一下代码,在查找后加入判断,如果没有找到目标则不进行删除,找到了再进行删除。如下:
s.erase(30);
for (auto e : s)
{
cout << e << " ";
}
cout << endl;
set<int>::iterator pos = s.find(30);
if(pos!=s.end())
{
s.erase(pos);
}
for (auto e : s)
{
cout << e << " ";
}
cout << endl;
传值传位置都可以,有什么区别呢?感觉传位置还麻烦一些啊,不如传值
确认值在不在就可以用第二种,不然就用删除值的,根据你的需求去选择合适的
🏀count

考虑这个数在不在的时候可以用count,不过不是为了这里设计的,为的是multiset,允许key值冗余,在这设计的原因是为了保持兼容一致。
🏀lower_bound&&upper_bound
lower_bound低边界的意思,要的是≥这个边界的值,upper_bound是高边界的意思,要的是<这个边界的值,可以说是一个左闭右开区间。测试代码如下:
void test_set2()
{
std::set<int> myset;
std::set<int>::iterator itlow, itup;
for (int i = 1; i < 10; i++)
myset.insert(i * 10); // 10 20 30 40 50 60 70 80 90
itlow = myset.lower_bound(25); // >= val
itup = myset.upper_bound(60); // > val //
cout << "["<<*itlow <<","<<*itup<<"]"<<endl;
myset.erase(itlow, itup); // 10 20 70 80 90
std::cout << "myset contains:";
for (std::set<int>::iterator it = myset.begin(); it != myset.end(); ++it)
std::cout << ' ' << *it;
std::cout << '\n';
}
效果如下:
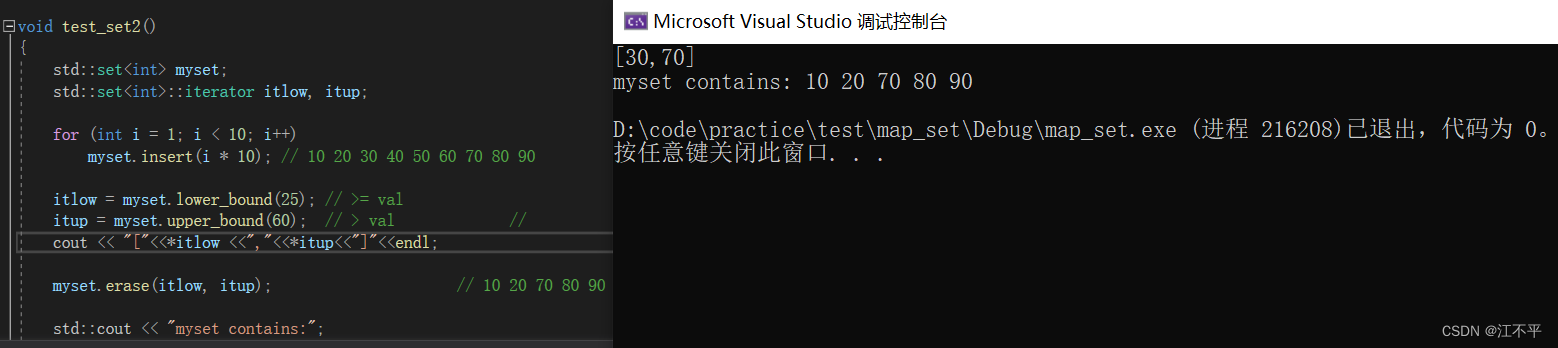
🏀equal_range
这里用到了pair键值对,详见下文里map部分内容。
如果所给数是35的话,则得到的是[40,40],如果是40的话,得到的是[40,50],由此可见区间左值要≥所给数,区间右值要>所给数。
void test_set3()
{
std::set<int> myset;
for (int i = 1; i <= 5; i++) myset.insert(i * 10); // myset: 10 20 30 40 50
std::pair<std::set<int>::const_iterator, std::set<int>::const_iterator> ret;
ret = myset.equal_range(40); // xx <= val < yy
std::cout << "the lower bound points to: " << *ret.first << '\n';
std::cout << "the upper bound points to: " << *ret.second << '\n';
}
🏐multipleset
真正的唯一区别就只有一个,允许键值冗余,用法上完全没有区别,会用set就会用multipleset
存储结构怎么存呢?
这里就不是遍历加去重了,单纯的排序
同时count和find也有点区别
例如find这里当有多个重复值时返回的是中序的第一个,count也不再只有0和1了,会显示个数,
🏐什么是map

底层存储的结构已经是pair了,pair是一个模板的键值对
pair的定义

第一个成员叫first第二个叫second
这两个的value type 的typedef是不一样的,pair的key对应的是const的key

make_pair就是构造一个匿名的pair返回,这样的话就可以去推导不用我们去写类型了,能方便一些。
拷贝和析构与set一样,底层是个树,代价还是挺大的
只要key有了就不允许插入,看key不看val,
make_pair的优势就是自动推导,好处就是不用显式的去写模板参数,那我们为什么不直接构造还调用这个函数,建立栈帧呢?不用担心,这个函数一般会定义成inline。
map的遍历
我们会发现报错,一个函数不会有两个返回值,当里面的数据是一个结构时
统计次数有这么几种方法
常规方法:
方括号:
这里的方括号与以前有些不同,以前相当于是给数组用的,用下标来随机访问,得益于底层空间是连续的,而这里是树形结构,肯定就不是来访问第几个了,这里是给一个key返回对应的value的引用,方括号一定程度上也代表了插入,如果说没有对应的映射类型,将会调用它的默认构造 (the element is constructed using its default constructor)
- 1.map中有这个key,返回value的引用(查找,修改)
- map中没有这个key,插入一个pair(key,value()),返回value的引用。(插入+修改)
跟at不一样,at只是查找加修改,如果没找到,就抛异常,而方括号的修改更加多元化。
以前我们写insert都是插入成功返回true,失败返回false,包括写二叉树搜索树都是,这里呢,是返回了个pair,
方括号的底层实现,相当于调用(*((this->insert(make_pair(k,mapped_type()))).first)).

上面那一大坨看起来很麻烦,我们先来看一下这里的insert
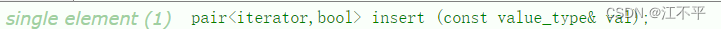
这里有个bool,就是说判断是否有这个key的,如果没有就插入
- 1.key已经在map中,返回pair(key_iterator,false);
- 2.key不在map中,返回pair(new_key_iterator,true);
了解了这些之后就可以把上面那个一大坨看起来很麻烦的简化一下
V& operator[const K & key]
{
pair<iterator,bool> ret = insert(make_pair(key,valur());
return ret.first->second;
}
所以我们更喜欢用方括号,功能多样,增改都有了,比起insert更喜欢用方括号来插入
🏐multimap
与map相比,没有方括号了,是因为允许键值冗余。find查找的是中序的第一个,其他基本差不多。
auto 用的前提是推导,右边的值推到左边,如果不能就别用auto
🏐相关问题
🏀topk问题(前k个高频单词)
前k个高频单词
思考:这个问题可以看到要求双排序,我们可以先统计次数。统计完之后我们要考虑topk,很多人都会想到堆,就是优先级队列,建一个大堆,依次去取,取出来后放进去,或者说小堆,但是小堆主要应对大量数据,这地方没必要,这里用优先级队列的话,有一个问题是不能保证出现次数相同的谁在前谁在后,重要的是字典序排序也很难。用优先级队列可不可以搞,可以,但还要上其他的东西或者说搞仿函数。优先级队列默认传的是小于,碰到次数相等尝试去比较key。
class Solution {
public:
struct Less
{
bool operator()(const pair<string,int>& kv1,const pair<string,int>& kv2) const
{
if(kv1.second<kv2.second)
{
return true;
}
if(kv1.second==kv2.second&&kv1.first>kv2.first)
{
return true;
}
return false;
}
};
vector<string> topKFrequent(vector<string>& words, int k) {
//统计次数
map<string,int> countMap;
for(auto&str: words)
{
countMap[str]++;
}
//topk
// priority_queue<pair<string,int>,vector<pair<string,int>>,Less<pair<string,int>>> maxHeap;
// for<auto& kv: countMap)
// {
// maxHeap.push(kv);
// }
typedef priority_queue<pair<string,int>,vector<pair<string,int>>,Less> MaxHeap;
MaxHeap mh(countMap.begin(),countMap.end());
vector<string> v;
while(k--)
{
v.push_back(mh.top().first);
mh.pop();
}
return v;
}
};
发现通过仿函数的方式用优先级队列也可以完成。
那我们用其他的方法呢?sort是不稳定的,我们改变它的比较方法让其稳定了,和上面那个优先级队列没啥区别都用到了仿函数,只是下面这个地方我们用到了算法
class Solution {
public:
struct Greater
{
bool operator()(const pair<string,int>& kv1,const pair<string,int>& kv2) const
{
if(kv1.second>kv2.second)
{
return true;
}
if(kv1.second==kv2.second&&kv1.first<kv2.first)
{
return true;
}
return false;
}
};
vector<string> topKFrequent(vector<string>& words, int k) {
map<string,int> countMap;
for(auto&str: words)
{
countMap[str]++;
}
for(auto&kv:countMap)
{
cout<<kv.first<<":"<<kv.second<<endl;
}
vector<pair<string,int>> sortv(countMap.begin(),countMap.end());
sort(sortv.begin(),sortv.end(),Greater());
vector<string> v;
for(size_t i=0;i<k;++i)
{
v.push_back(sortv[i].first);
}
return v;
}
};
1.这个地方sort也可以换成stable_sort,这样仿函数就不用多比较一下。2.算法需要随机迭代器所以这个地方用vector转了一下。
那如果不用仿函数可以做吗?我们要进行排序,除了考虑排序算法我们还可以考虑map和set,只不过是对key排序,但是这里不能用map是因为,map是去重+排序,所以要用multimap
class Solution {
public:
vector<string> topKFrequent(vector<string>& words, int k) {
//统计次数,默认按string去排序
map<string,int> countMap;
for(auto&str: words)
{
countMap[str]++;
}
multimap<int,string,greater<int>> sortMap;
for(auto&kv:countMap)
{
sortMap.insert(make_pair(kv.second,kv.first));
}
vector<string> v;
multimap<int,string,greater<int>>::iterator it=sortMap.begin();
for(size_t i=0;i<k;++i)
{
v.push_back(it->second);
++it;
}
return v;
}
};
注意这里它是中序来比较,有的人觉得我这里排降序,然后用反向迭代器也可以,但是在multimap时已经按字典序排过了,倒着取就不对了。
这个地方同stablesort是一样的,保证稳定是保证次数相同的稳定。
🏀两个数组的交集
两个数组的交集
判断在不在另一个数组里呢?肯定是用set更好,因为它快啊,比我们直接去用find快,算法里也有find但是是暴力查找,复杂度为O(N),另一个是O(lgN)。
放进set去重,记住!!搞交集一定要去重,因为如下两个数组nums1 = [1,2,2,1], nums2 = [2,2],当2去第一个数组里查时发现重复所以放到vector里,那当第二个2去查时也会发现重复又放到vector里,所以一定要去重!!
当然算法里也有个东西可以做到去重,叫unique,这是去重算法,你可以先sort一下,再unique。这个是没有删除元素的,是通过覆盖的方式,最后resize一下实现的,这也在刚学习数据结构时顺序表部分有类似操作。
这里我们搞个新思路,不用在不在的思想,假设已经去过重了,交集差集怎么得到呢?这里有个算法思想可以很好的解决这个问题。
两个下标位置依次走
找交集
1.小的++
2.相等的就是交集,同时++
3.其中一个结束了,交集就找完了
找差集
1.小的就是差集
2.相等就同时++
3.其中一个结束了,另一个剩下的部分就是差集
class Solution {
public:
vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
set<int> s1(nums1.begin(),nums1.end());
set<int> s2(nums2.begin(),nums2.end());
auto it1=s1.begin();
auto it2=s2.begin();
vector<int> v;
while(it1!=s1.end()&&it2!=s2.end())
{
if(*it1<*it2)
{
++it1;
}
else if(*it2<*it1)
{
++it2;
}
else
{
v.push_back(*it1);
++it1;
++it2;
}
}
return v;
}
};
💬总结
- 找交集时一定要记得去重!!


![[算法沉淀记录] 排序算法 —— 归并排序](https://img-blog.csdnimg.cn/direct/6197831ecff54a60b21edb31f9c2120a.png)