BM42 用两个栈实现队列 easy

import java.util.Stack;

public class Solution {
    Stack<Integer> stack1 = new Stack<Integer>();
    Stack<Integer> stack2 = new Stack<Integer>();
    
    public void push(int node) {
        stack1.push(node);
    }
    
    public int pop() {
        if(stack2.isEmpty()){
            while(!stack1.isEmpty()){
                stack2.push(stack1.pop());
            }
        }
        return stack2.pop();
    }
}

时间复杂度O(N),空间复杂度O(1)

BM43 包含min函数的栈 easy

import java.util.Stack;

public class Solution {
    Stack<Integer> min=new Stack<>();
    Stack<Integer> s=new Stack<>();
    
    public void push(int node) {
        s.push(node);
        if(min.isEmpty()){
            min.push(node);
        }else if(node<=min.peek()){
            min.push(node);
        }
    }
    
    public void pop() {
        int node=s.pop();
        if(node==min.peek()){
            min.pop();
        }
    }
    
    public int top() {
        return s.peek();
    }
    
    public int min() {
        return min.peek();
    }
}

BM44 有效括号序列 easy

import java.util.*;


public class Solution {
    /**
     * 
     * @param s string字符串 
     * @return bool布尔型
     */
    public boolean isValid (String s) {
        // write code here
        Stack<Character> stack=new Stack<>();
        for(int i=0;i<s.length();i++){
            char ch=s.charAt(i);
            if(ch=='['||ch=='{'||ch=='('){
                stack.push(ch);
            }else if(!stack.isEmpty()){
                if(ch==')'&&stack.peek()=='('){
                    stack.pop();
                }else if(ch==']'&&stack.peek()=='['){
                    stack.pop();
                }else if(ch=='}'&&stack.peek()=='{'){
                    stack.pop();
                }else{
                    return false;
                }
            }else{
                return false;
            }
        }
        return stack.isEmpty();
    }
}

BM45 滑动窗口的最大值 hard

import java.util.*;
public class Solution {
    public ArrayList<Integer> maxInWindows(int [] num, int size) {
        //这么写会报错，因为题目要求返回ArrayList<>
        //List<Integer> res=new ArrayList<>();
        ArrayList<Integer> res=new ArrayList<>();
        if(size<=num.length&&size!=0){
            //创建双向队列
            Deque<Integer> dq=new ArrayDeque<>();
            //先处理第一个滑动窗口的数据
            for(int i=0;i<size;i++){
                //如果num[i]大于dq中的数据,则删除
                if(!dq.isEmpty()&&num[dq.peekLast()]<num[i])
                    dq.pollLast();
                dq.add(i);
            }
            //比如num为{2,4,3,1,6}，size为3
            //则第一个for循环后的结果为dq{4,3}
            
            for(int i=size;i<num.length;i++){
                //将dq.peekFirst()对应的数值写入res
                res.add(num[dq.peekFirst()]);
                //如果dq.peekFirst出了滑动窗口，则退出队列
                if(!dq.isEmpty()&&dq.peekFirst()<(i-size+1))
                    dq.pollFirst();
                //如果num[i]大于dq中的数据，则删除
                while(!dq.isEmpty()&&num[dq.peekLast()]<num[i])
                    dq.pollLast();
                dq.add(i);
            }
            res.add(num[dq.pollFirst()]);
        }
        return res;
    }
}

题目要求时间复杂度O(N),空间复杂度O(N)
使用双向队列

关于ArrayDeque的常用方法

Modifier and Type Method and Description
boolean add(E e)
在此deque的末尾插入指定的元素。
void addFirst(E e)
在此deque前面插入指定的元素。
void addLast(E e)
在此deque的末尾插入指定的元素。
void clear()
从这个deque中删除所有的元素。
ArrayDeque clone()
返回此deque的副本。
boolean contains(Object o)
如果此deque包含指定的元素，则返回 true 。
Iterator descendingIterator()
以相反的顺序返回此deque中的元素的迭代器。
E element()
检索，但不删除，由这个deque表示的队列的头。
E getFirst()
检索，但不删除，这个deque的第一个元素。
E getLast()
检索，但不删除，这个deque的最后一个元素。
boolean isEmpty()
如果此deque不包含元素，则返回 true 。
Iterator iterator()
返回此deque中的元素的迭代器。
boolean offer(E e)
在此deque的末尾插入指定的元素。
boolean offerFirst(E e)
在此deque前面插入指定的元素。
boolean offerLast(E e)
在此deque的末尾插入指定的元素。
E peek()
检索但不删除由此deque表示的队列的头部，如果此deque为空，则返回 null 。
E peekFirst()
检索但不删除此deque的第一个元素，如果此deque为空，则返回 null 。
E peekLast()
检索但不删除此deque的最后一个元素，或返回 null如果此deque为空）。
E poll()
检索并删除由此deque（换句话说，该deque的第一个元素）表示的队列的 null如果此deque为空，则返回 null 。
E pollFirst()
检索并删除此deque的第一个元素，如果此deque为空，则返回 null 。
E pollLast()
检索并删除此deque的最后一个元素，如果此deque为空，则返回 null 。
E pop()
从这个deque表示的堆栈中弹出一个元素。
void push(E e)
将元素推送到由此deque表示的堆栈上。
E remove()
检索并删除由此deque表示的队列的头部。
boolean remove(Object o)
从此deque中删除指定元素的单个实例。
E removeFirst()
检索并删除此deque的第一个元素。
boolean removeFirstOccurrence(Object o)
删除此deque中指定元素的第一个出现（从头到尾遍历deque时）。
E removeLast()
检索并删除此deque的最后一个元素。
boolean removeLastOccurrence(Object o)
删除此deque中指定元素的最后一次（从头到尾遍历deque时）。
int size()
返回此deque中的元素数。
Spliterator spliterator()
创建一个late-binding和失败快速 Spliterator在这个deque的元素。
Object[] toArray()
以适当的顺序返回一个包含此deque中所有元素的数组（从第一个到最后一个元素）。
T[] toArray(T[] a)
以正确的顺序返回一个包含此deque中所有元素的数组（从第一个到最后一个元素）; 返回的数组的运行时类型是指定数组的运行时类型。

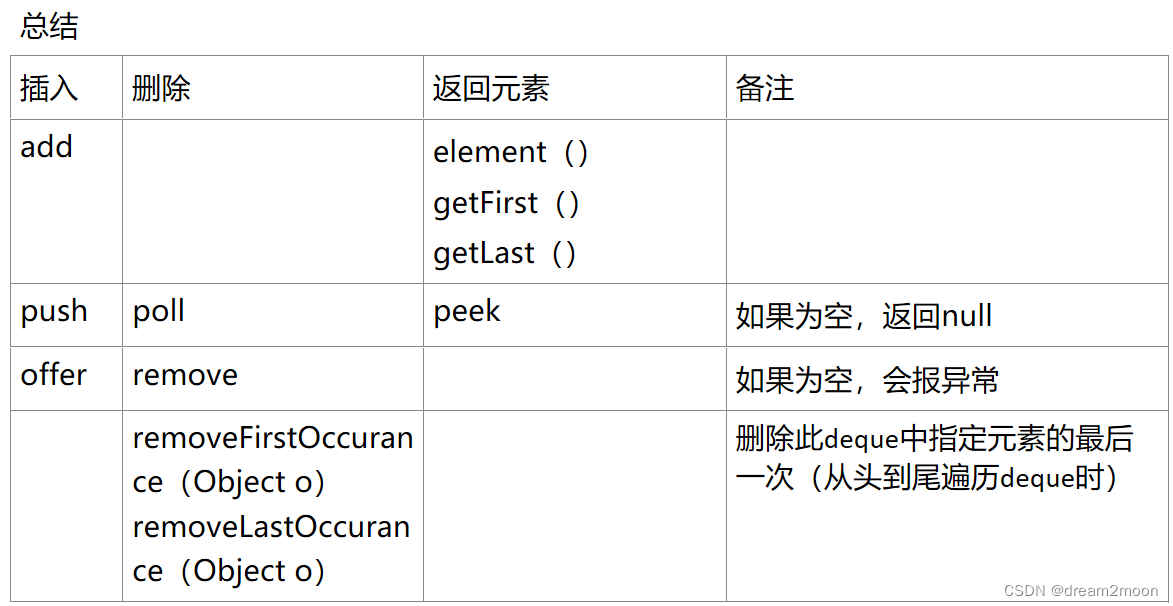
插入删除方法总结

BM46 最小的K个数 medium

import java.util.*;
public class Solution {
    public ArrayList<Integer> GetLeastNumbers_Solution(int [] input, int k) {
        ArrayList<Integer> res = new ArrayList<Integer>();
        //排除特殊情况
        if(k == 0 || input.length == 0) 
            return res;
        //大根堆 
        PriorityQueue<Integer> q = new PriorityQueue<>((o1, o2)->o2.compareTo(o1));
        //构建一个k个大小的堆  
        for(int i = 0; i < k; i++)
            q.offer(input[i]);
        for(int i = k; i < input.length; i++){
            //较小元素入堆
            if(q.peek() > input[i]){  
                q.poll();
                q.offer(input[i]);
            }
        }
        //堆中元素取出入数组
        for(int i = 0; i < k; i++) 
            res.add(q.poll());
        return res;
    }
}

大根堆，小根堆
题目要求时间复杂度O(nlogk),空间复杂度O(n)

创建大根堆

//大根堆 
        PriorityQueue<Integer> q = new PriorityQueue<>((o1, o2)->o2.compareTo(o1));

这是用到了lambda表达式

// 1. 不需要参数,返回值为 2
() -> 2
// 2. 接收一个参数(数字类型),返回其2倍的值
x -> 2 * x
// 3. 接受2个参数(数字),并返回他们的和
(x, y) -> x + y
// 4. 接收2个int型整数,返回他们的乘积
(int x, int y) -> x * y
// 5. 接受一个 string 对象,并在控制台打印,不返回任何值(看起来像是返回void)
(String s) -> System.out.print(s)