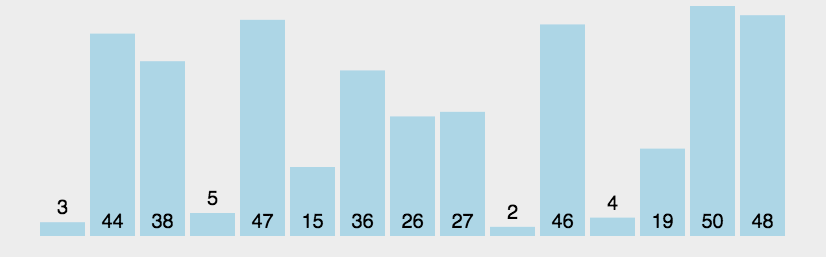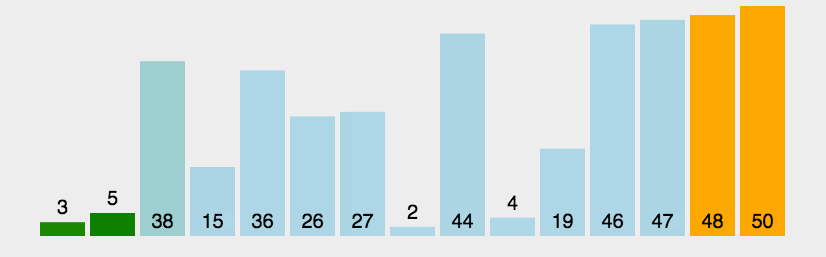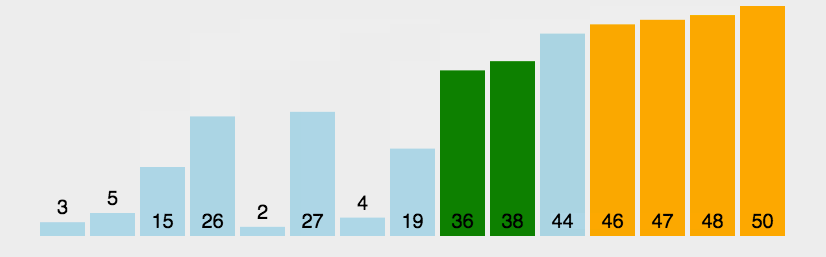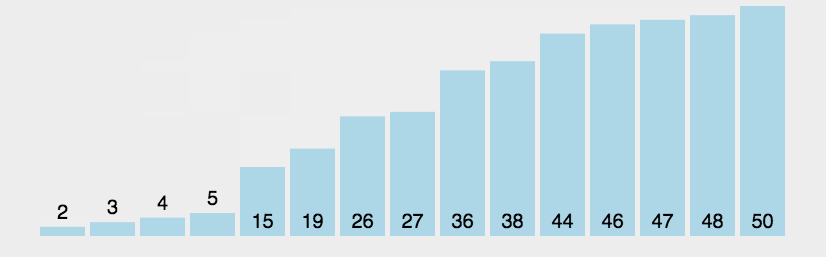目录
1. 前言
2. Minimax算法介绍
2.1 博弈树
2.2 估值函数
2.3 基本算法思想
2.4 实例1
2.5 实例2—棋类游戏
2.6 小结
3. Tic-Tac-Toe minimax AI实现
3.1 函数说明
3.2 处理流程
3.3 代码
4. 小结
1. 前言
在上一篇中实现一个简单的Tic-Tac-Toe人机对弈程序。参见:
Tic-Tac-Toe人机对弈程序(python实现)_笨牛慢耕的博客-CSDN博客前面几篇博客(以循序渐进的方式)实现了Tic-Tac-Toe游戏的棋局搜索、遍历以及所有可能棋局数和盘面状态数的计算,参见:本文先实现一个简单的Tic-Tac-Toe人机对弈程序,为下一步实现基于minimax算法的Tic-Tac-Toe人机对弈程序做一个准备。https://blog.csdn.net/chenxy_bwave/article/details/128555550 其中计算机棋手或者说AI棋手除了在下一步能够使自己获胜或者阻止对手取胜外,就只是随机落子了。本文更进一步引入经典的经典的对抗性博弈算法minimax算法来为AI棋手加持。
2. Minimax算法介绍
2.1 博弈树
解决博弈类问题的一般方法是将游戏状态组织成一棵树,树的每一个节点表示一种状态(比如说棋类游戏中的棋盘盘面状态),而父子关系表示由父节点经过一步可以到达子节点。边则用于表示动作。
Minimax也不例外,以棋类游戏为例,树形结构的奇数层(初始状态、即根节点所在层为第1层)表示轮到先手方下棋;偶数层则轮到后手方下棋的状态。Minimax就是针对这个树形结构进行搜索最优解的算法。奇数层称为极大值(己方)层(简称max层,其中的节点则称为max节点),偶数层称为极小值(对方)层(相应地,min层,min节点)。
2.2 估值函数
估值函数用来给每一个局面给出一个估值,用于判断博弈树中当前局面的形势。在传统的棋类游戏智能系统中,估值函数一般是人为指定的,对棋类游戏智能的水平有决定性作用。
估值函数的形式不是固定的,它的输入一般是一个局面的信息,输出是一个表明相应局面好坏程度的数值,比如说胜率之类的。
比如说,在井字棋中估值函数的1个例子:玩家X还存在可能性的行、列、斜线数减去玩家O还存在可能性的行、列、斜线数。如下图所示,玩家X还存在可能性的行、列、斜线数为6,玩家O还存在可能性的行、列、斜线数为3,因此估值函数在图3局面下的输出为3。当然也可以是两个数的比值,或者别的什么函数关系。。。

以上这个例子可以成为井字棋的一种启发式估值函数。估值函数也可以来自蒙特卡洛仿真,即通过大量的随机仿真,统计从某个局面出发所有可能的棋局中的胜负结果,由此来决定该局面的评分(价值估计)。
游戏或者棋局的终局局面的价值估计就相对简单一些,通常可以直接进行启发式的定义。
2.3 基本算法思想
Minimax算法(中文译名为极小化极大算法)常用于棋类等由两方较量的游戏的智能搜索算法。该算法是一个零和(zero-sum)算法,即站在游戏的一方来看,自己要在可选的选项中选择将己方优势最大化的选择;而对手则要选择令己方优势最小化的方法。在两人棋类游戏中,例如五子棋、象棋、国际象棋、井字棋(tic-tac-toe)、围棋,由两个player交替走棋,每次走一步。这些游戏的智能程序的开发就可以用到Minimax算法。
举个例子,两个人下棋。当前该下棋的一方(称为己方或我方,与之相对的玩家称为对手方)的下一手棋有N种选择:,分别导致己方的胜率分别为
。那己方的选择自然应该是:
反之,轮到对手方下棋时自然就是要选择能够使得己方的胜率最小化(由于是零和游戏,己方胜率最小化自然就对应着对手方胜率最大化)的落点或者招法。
Minimax是一种悲观算法,它假设对手具有完美决策能力,对手每一步都会从当前局面将我方引入理论上胜率最小的盘面状态。己方策略则应该是选择那些对方所能达到的让我方最差情况中最好的,也就是让对方在完美决策下所对己方造成的损失最小。具体一点说,假设当前盘面状态下,己方有N种选择:,分别导致
的盘面状态。在各
状态下,对手方采取最优策略(针对每个
都下出使得己方胜率最小—损失最大—的棋)下导致己方的胜率分别为
,则己方应该选择的着法由
决定.
2.4 实例1
本例取自参考博客[2]。
现在考虑这样一个游戏:有三个盘子A、B和C,每个盘子分别放有三张纸币。A放的是1、20、50;B放的是5、10、100;C放的是1、5、10。游戏参与者为甲、乙两人,三个盘子的信息对于两人都是完全可见的。游戏分三步:
- 甲从三个盘子中选取一个。
- 乙从甲选取的盘子中拿出两张纸币交给甲。
- 甲从乙所给的两张纸币中选取一张。
游戏中,甲的目标是最后拿到的纸币面值尽量大,乙的目标是让甲最终拿到的纸币面值尽量小(注意,这里,乙的目标并不是自己最后拿到的面值最大化!如果游戏目标改为使乙获得的面值最大化或者最小化,或者说使得甲所获得的面值最小化,则成了另外的三个游戏,所得的解是不同的)。
基于minimax算法对以当前节点为根的游戏状态节点树进行搜索来确定下一步的选择的处理步骤如下:
(1)根据游戏规则(甲、乙双方交替动作)构建状态节点树;
(2)确定各底层叶子的价值
(3)从底层叶子开始由底向上根据minimax原则进行节点价值更新
(4)基于根节点的节点价值更新决策(即选择子节点中最大值)决定当前状态下的下一步
这种基于minimax原则构建出来的搜索树可以称为minimax(搜索、博弈决策)树。
本问题中,每个节点的价值定义是显而易见的,可以定义为游戏从该节点所表示的状态出发在最优情况下甲可以得到的面值。在max层要使得节点价值最大化,而min层则要使得节点价值最小化。
下图是上述示例问题的状态树:

站在甲的角度来考虑。其中正方形节点表示轮到我方(甲)操作,而三角形表示轮到对方(乙)操作。经过三轮动作后(我方-对方-我方),到达终局状态(表示终局状态的节点由于是叶子节点,所以不需要做MIN/MAX区分)。黄色叶结点表示所有可能的结局。从甲方看,由于最终的收益可以通过纸币的面值评价,我们自然可以用终局时甲方拿到的纸币面值表示终局状态的价值。
下面考虑倒数第二层节点,这一层是所谓的极大值层,即轮到甲方选择操作,选择的结果应该是使得节点的价值最大化。即每个节点的价值为其各子节点价值的最大值,由此可得该层的价值如下所示:

倒数第三层为极小值层,轮到乙方选择。如前所述,乙方选择的目的是使得节点价值最小化,因此这些节点的价值取决于子节点的最小值。
最后,根节点是max节点,因此价值取决于叶子节点的最大值。最终完整赋值的minimax树如下所示:
由此可见,该游戏的结果是甲可以得到面值为20的纸币。其前提是游戏双方均有完美决策能力。在实际对弈等游戏中,游戏参与者可能没有完美决策能力,有一定概率会做出非最优的选择,这种情况下的游戏就会出现更多更丰富的变化。
在本示例问题可能的状态数非常少,因此可以通过暴力枚举的方式给出完整的状态树。这种情况下可以基于Minimax算法得出全局最优解。在现实世界的问题中,状态树通常非常庞大,即使是计算机也难以或者不可能给出完整的树,这种情况下往往需要限定搜索深度,所得到的解为局部最优解,可能会与全局最优解有所偏差。
2.5 实例2—棋类游戏
本例取自参考博客[3]。
以下以两人对战的棋类游戏为例来说明。
前面说过,基于树的搜索问题的首要关键点是节点价值(函数)的定义。
在以上的例子中是直接以甲可以得到的纸币面值作为各节点的价值。而且,由于只有三个回合(注意,本文中回合对应一手棋,而不是各下一手),所以可以合理地假定游戏双方都可以向前计算三步直到游戏结果(look ahead to the end of game)。这意味着游戏双方一开始就知道完整的minimax树。
在棋类游戏中,棋局的最终结果只有(站在其中一方来看)胜和负两种结果,所以,很自然地,终局状态节点可以考虑用{1,0, -1}来表示{胜,平,负}用作节点的价值函数。但是棋局中间状态的价值估计就要更复杂一些,一般来说可以用胜率(在很难或者无法确认每个节点的胜负情况下,通常与蒙特卡洛方法结合)来定义价值函数,或者别的启发式方法—这是后话,以后再讨论。
除了胜负结果以外,还可以考虑其它的特征用于节点价值的定义。以下假设节点价值估计函数已经定义好了。
进一步,即便以Tic-Tac-Toe(3x3井字棋)这样简单的游戏来说,最长可能需要9个回合。这样所导致搜索树的深度最多为10,再考虑到branching factor,这种规模的树(上一篇我们得出了Tic-Tac-Toe总共有26830种棋局的结果了)已经超出了绝大多数人类的大脑计算能力了(当然对于计算机来说这个仍然是轻而易举的)。所以,对于非完美player(比如说正常的人类棋手)来说,假定计算深度(the steps of looking-ahead)是有限的(小于最大棋局步数)是一个合理的假设。
基于以上假设在棋局对弈过程大抵可以描述如下。
首先,考虑最简单的情况,假设棋手只能向前看一步(计算深度为1,looking ahead by 1 step)。这种情况下:轮到甲方(先手方,即当前为max层)下棋时,棋手基于当前局面确定自己可能走的下一步棋,预测了自己走完这一步的所有可能的局面,然后针对各个局面进行价值评估(这里假定价值评估是可能的,是否合理或者最优是另外一个问题),然后从中选择其中价值最大者(换言之使得先手方胜率最低)所对应的走法。轮到乙方(对手方,后手方)下棋时,乙方也预测了自己走完这一步的所有可能的局面,然后也选择了所有走法中局面看起来最好的(价值函数最小的,换言之使得先手方胜率最低)走法。如此循环往复,直到最后游戏结束。注意,由于假定双方的计算深度只有一步,因此各自决定自己下一手走哪儿时,只考虑了自己可选的落点所导致的局面,并没有考虑对手方针对自己的落点的应手。
考虑对弈双方的计算深度为2,情况会怎么样呢?
轮到甲方(先手方,即当前为max层)下棋时,先手预测了自己走完这一步的所有可能局面{},进一步预测了对手针对每种局面的所有可能应对方案得到所有可能的局面为{{
}, {
}, ..., {
}}。考虑先手方是要使得盘面状态价值最大,而后手方是要使得盘面状态价值最小,因此先手方的决策过程如下图所示,由此得出最优的k_opt如图中所示。

轮到后手方走也是如此,只不过是反过来的,后手方的决策方程为:

通俗一点说,就是:我猜到了我这么走,你会怎么走,所以我选择这么走。
如果双方的计算深度为3的话,情况就更加复杂了:先手预测了自己走完这一步的所有可能局面,并同时预测了对手的所有应对方案,还同时又想到了自己在面对对手的每种应对方案时的所有可能走法,然后从中选择一个最优的。后手也是如此。也就是,我猜到了我这么走你会那么走然后我会那么那么走,所以我选择这么走。。。
我们用正方形来代表max层节点(即轮到先手方行棋,行棋目标是使当前节点价值最大化),圆形来代表min层节点(即轮到后手方行棋,行棋目标是使当前节点价值最小化)。叶子节点代表终局状态,有对应的预设的价值(比如说,用1代表赢棋,-1或者0代表输棋)。
假设对弈棋手计算深度为4,即可以向前看4步,则先手看到的一个部分博弈树(“部分”是因为还没有到达终局)的示例如下所示则我们假设棋局的博弈树如下(往后看4步)。根据这个博弈树(我们假定已知这个博弈树的“叶子”节点的价值估计),先手在当前状态下应该如何选择呢:
首先,先手应该计算后手在第四步的时候所得到的各种局面的价值估计(启发式或者别的什么方式来确定。因为这是部分搜索树的叶子节点,所以不是基于子节点价值进行min/max估计),如下图(最底下一层):

然后先手再计算自己在第三步时应该如何选择(即从所有子节点中选择最大的),如下图(红色字体):

然后先手再计算后手在第二步时应该如何选择(即从所有子节点中选择最小的),如下图(红色字体):

最后先手就可以当前局面下下一步应该怎么走了(即从所有子节点中选择最大的),如下图(根节点):

所以,如果先后手都进行最优决策的话,棋局的走向则下图所示(红线):
当然,如果后手不是进行最优决策的话,棋局的走向就不一定是这样的了,先手也可以尝试走有风险但是可能收益更高的局面(类似于“骗招”性质的招法。骗招中的“骗”意味着假定对手不能进行最优决策,这样可以得到比双方都下最优招法能得到更大的便宜。但是一旦对手识破了骗招而下出了最优招法,那下骗招一方反而会招致更大的损失),这就不在我们的讨论范围之内了。以上讨论可以看到,按照MiniMax算法来进行决策的话,需要的计算量是随着计算深度(向前看的步数)的增加而呈指数级增长的。计算深度越大自然棋力就越高,胜率越高。但是,这些状态中其实是包含很多不必要的状态的,所以我们可以通过剪枝操作进行优化。
2.6 小结
总结一下Minimax算法的要点:
- 确定最大搜索(计算)深度D,经过深度为D的minimax搜索的构建,可能达到终局,也可能只能到达一个中间状态。对于简单问题可以直接从游戏初始状态出发构建出完整的minimax搜索树,但是真实问题一般无法构造出完整的状态树,所以需要确定一个最大深度D,每次最多从当前状态向下计算D层。
- 基于当前状态(以当前状态节点为根节点)构建深度为D+1的部分搜索树(也称博弈决策树)
- 针对该部分搜索树的叶子节点进行价值估计(使用预定义的价值估计值,或者。。。。比如说,实际对弈过程中,人类棋手根据经验和棋感对局面进行胜率评估)
- 自底向上为非叶子节点赋值。其中max节点取子节点最大值,min节点取子节点最小值。根节点赋值完毕后即完成了minimax搜索树的构建
根节点赋值的决策自然就决定当前状态下的下一手,从根结点选择子节点中价值最大的分支,作为行动策略。下图所示为Tic-Tac-Toe游戏中一个可能的minimax搜索树的样子[3]:

Tic-Tac-Toe游戏的一个minimax搜索树例
如果可以从游戏初始状态出发构建出完整的minimax搜索树,则minimax算法可以给出全局最优解。这种情况可以称为complete-minimax。
在搜索深度有限(小于完整的游戏所需要的步数),只能构建出部分minimax搜索树(这个称为partial-minimax),所得到的解可以看作是一个局部最优解。搜索深度越大越可能找到更好的解,但计算耗时会以指数的方式膨胀。在搜索深度有限的条件下,Minimax算法的应用一般是边对弈、边计算局部minimax搜索树,类似于sliding-window的工作方式。
3. Tic-Tac-Toe minimax AI实现
以下代码是基于上一篇(Tic-Tac-Toe人机对弈程序(python实现))中的代码进行改进的。主要是追加了由函数nextMove_complete_minimax()实现的minimax AI agent。以及其它一些相关联的修改,和一些代码优化,详细参见以下代码中的说明。
3.1 函数说明
函数原型:nextMove_complete_minimax (board, isMax, player)
【Input】
board: 当前盘面状态。
isMax: 当前层是MAX层还是MIN层。注意,是站在当前玩家的角度来看。在递归调用时要注意切换。
player: 轮到行棋的当前玩家。
【Ret】
bestMove:对于当前玩家来说的最佳下一手
bestScore:下完bestMove后的局面的评分(价值估计)
3.2 处理流程

3.3 代码
# Tic Tac Toe
# Created by chenxy in 2017-06-23, with only drawBoard() copied from <<inventwithpython>>
# 2023-01-04 refined,rev0
# 2023-01-07 refined,rev1
# (1) Add minimax AI agent, nextMove_complete_minimax()
# (2) askGameStart() updated to support AI agent selection
# (3) gameRole --> GAME_ROLE, used as global constant
# (4) askNextMove() renamed to naiveAiNextMove(), in contrast with minimax-AI
# (5) Main program updated in accordance with the added minimax AI
# (6) Other miscellaneous editorial refinement
# 2023-01-07 rev2
# (1) Correct a bug in gameJudge()
# (2) Add layer parameter for the convenience of debug
# (3) Refine the debug message print, with DEBUG for switch on/off debug msg print
import random
import sys
GAME_ROLE = ['A','H']; # 'A': AI; 'H': Human;
DEBUG = 0
def drawBoard(board, initFlag = 0):
# This function prints out the board that it was passed.
brd_copy = board.copy()
if initFlag:
brd_copy = ['0','1','2','3','4','5','6','7','8','9']
# "board" is a list of 10 strings representing the board (ignore index 0)
print('=============')
# print(' | |')
print(' ' + brd_copy[7] + ' | ' + brd_copy[8] + ' | ' + brd_copy[9])
# print(' | |')
print('-----------')
# print(' | |')
print(' ' + brd_copy[4] + ' | ' + brd_copy[5] + ' | ' + brd_copy[6])
# print(' | |')
print('-----------')
# print(' | |')
print(' ' + brd_copy[1] + ' | ' + brd_copy[2] + ' | ' + brd_copy[3])
# print(' | |')
print('=============')
print()
def askGameStart():
# Ask human start a game or not;
# print('Do you want to start a game? Y or y to start; Others to exit');
# inputWord = input().lower();
# if inputWord.startswith('y'):
# startNewGame = True;
# else:
# startNewGame = False;
print('Start a new game? Press 1 to start; Others to exit');
cmd = input()
if cmd.isdigit():
inputWord = int(cmd);
if inputWord == 1:
startNewGame = True;
else:
startNewGame = False;
else:
startNewGame = False;
aiAlgo = 0
if startNewGame:
print('Please select the AI agent to fight with: [1] Unbeatable minimax AI; [0] naive AI(default);');
cmd = input()
if not cmd.isdigit():
aiAlgo = 0
else:
if int(cmd)==1:
aiAlgo = 1
return startNewGame, aiAlgo
# Decide whether the number human input for the next move has been already used or not.
# It can be decided by whether the corrsponding element is empty or not.
def isValidInput(board, humanNextMove):
isValid = 1;
if humanNextMove == 0:
print('Please input 1~9, 0 is not an valid input for the next move!');
isValid = 0;
elif board[humanNextMove] != ' ':
print('The space has already been used! Please select an empty space for the next move');
isValid = 0;
return(isValid);
# Ask the human player for the next move.
def askHumanNextMove(board):
while True:
print('Please input the next move!');
c = input()
if not c.isdigit():
print('Invalid input! Please input [1-9]!');
continue
nextMove = int(c);
if board[nextMove] == ' ':
break;
else:
print('Stone already in this grid! Please input again!');
continue;
isValid = isValidInput(board, nextMove)
return isValid,nextMove
def gameRsltDisplay(winner):
if 'A' == winner:
print('AI win!');
elif 'H' == winner:
print('Human win!');
else:
print('A tie game!');
# Decide AI's next move.
# Decide whether the three input are all the same
def isTripleGoalReachedNext(board, idx1, idx2, idx3, role):
in1 = board[idx1];
in2 = board[idx2];
in3 = board[idx3];
if in1 == ' ' and in2 == in3 and in2 == role:
return idx1;
elif in2 == ' ' and in1 == in3 and in3 == role:
return idx2;
elif in3 == ' ' and in1 == in2 and in1 == role:
return idx3;
else:
return 0; # Invalid space index.
def isGoalReachedNext(board, player):
nextMove = 0;
nextMove = isTripleGoalReachedNext(board, 1, 4, 7, GAME_ROLE[player]);
if nextMove > 0:
return True, nextMove
nextMove = isTripleGoalReachedNext(board, 1, 2, 3, GAME_ROLE[player]);
if nextMove > 0:
return True, nextMove
nextMove = isTripleGoalReachedNext(board, 1, 5, 9, GAME_ROLE[player]);
if nextMove > 0:
return True, nextMove
nextMove = isTripleGoalReachedNext(board, 2, 5, 8, GAME_ROLE[player]);
if nextMove > 0:
return True, nextMove
nextMove = isTripleGoalReachedNext(board, 3, 5, 7, GAME_ROLE[player]);
if nextMove > 0:
return True, nextMove
nextMove = isTripleGoalReachedNext(board, 3, 6, 9, GAME_ROLE[player]);
if nextMove > 0:
return True, nextMove
nextMove = isTripleGoalReachedNext(board, 4, 5, 6, GAME_ROLE[player]);
if nextMove > 0:
return True, nextMove
nextMove = isTripleGoalReachedNext(board, 7, 8, 9, GAME_ROLE[player]);
if nextMove > 0:
return True, nextMove
return False, nextMove;
def naiveAiNextMove(board):
# Temporarily, select the first empty space.
# 1. First, check whether AI will reach the goal in the next step.
# GAME_ROLE[0] represents AI's role.
goalReachedNext, nextMove = isGoalReachedNext(board, 0);
if goalReachedNext == True:
return nextMove;
# 2. Secondly, check whether Human will reach the goal in the next step.
# GAME_ROLE[1] represents Human's role.
# Of course, AI should take the next move to blocking Human player to reach the goal.
goalReachedNext, nextMove = isGoalReachedNext(board, 1);
if goalReachedNext == True:
return nextMove;
# Randomly selected from the left spaces for the next move.
spaces = []
for k in range(1,10):
if board[k] == ' ':
spaces.append(k)
else:
continue;
nextMove = random.choice(spaces)
return(nextMove);
def nextMove_complete_minimax(board, isMax, player, layer):
'''
Minimax algorithm for tic-tac-toe
Decide the next move according to complete minimax algorithm for the current player
board: Current board status, char array of 10 elements, ignoring [0]
isMax: Is this eithe MAX of MIN layer for the current player
True: MAX layer
False: MIN lafyer
player: int
0: Player represented by GAME_ROLE[0]
1: Player represented by GAME_ROLE[1]
'''
if DEBUG:
print('{0}Enter minimax(): board={1}, isMax={2}, player={3}'.format(layer*'+',board,isMax,player))
bestScore = -1000 if isMax else 1000
nextPlayer = 1 if player==0 else 0
bestMove = 0
# game over judge
gameOver, winner = gameJudge(board)
if gameOver:
if winner == ' ': # DRAW or TIE game
bestScore = 0
if DEBUG:
print('{0}GameOver: winner={1}, bestMove={2}, bestScore={3}'.format(layer*'+',winner,bestMove,bestScore))
return bestMove,bestScore
else:
# If it is the end of game, then it must be the win of the opponent.
bestScore = (-1 if isMax else 1)
if DEBUG:
print('{0}GameOver: winner={1}, bestMove={2}, bestScore={3}'.format(layer*'+',winner,bestMove,bestScore))
return bestMove,bestScore
for k in range(1,10):
if board[k] == ' ':
board[k] = GAME_ROLE[player]
move, score = nextMove_complete_minimax(board, (not isMax), nextPlayer, layer+1)
board[k] = ' ' # Recover board status
if isMax:
if score > bestScore:
bestScore = score
bestMove = k
else:
if score < bestScore:
bestScore = score
bestMove = k
if DEBUG:
print('{0}Exit minimax(): bestMove={1}, bestScore={2}'.format(layer*'+',bestMove,bestScore))
return bestMove, bestScore
# Decide whether the three input are all the same
def isTripleSame(in1, in2, in3):
if in1 == ' ' or in2 == ' ' or in3 == ' ':
return False
elif in1 == in2 and in1 == in3:
return True
else:
return False
def gameJudge(board):
if isTripleSame(board[1],board[4],board[7]):
gameOver = True; winner = board[1];
elif isTripleSame(board[1],board[2],board[3]):
gameOver = True; winner = board[1];
elif isTripleSame(board[1],board[5],board[9]):
gameOver = True; winner = board[1];
elif isTripleSame(board[2],board[5],board[8]):
gameOver = True; winner = board[2];
elif isTripleSame(board[3],board[5],board[7]):
gameOver = True; winner = board[3];
elif isTripleSame(board[3],board[6],board[9]):
gameOver = True; winner = board[3];
elif isTripleSame(board[4],board[5],board[6]):
gameOver = True; winner = board[4];
elif isTripleSame(board[7],board[8],board[9]):
gameOver = True; winner = board[7];
elif ' ' in board[1:10]:
gameOver = False; winner = ' ';
else:
gameOver = True; winner = ' ';
return gameOver, winner
whoseTurn = 0; # 0 : AI's turn; 1: Human's turn.
board = [' ']*10; # Note: '*' for string means concatenation.
drawBoard(board,1); # Draw the initial board with numbering
while True:
startNewGame, aiAlgo = askGameStart()
if not startNewGame:
print('Bye-Bye! See you next time!');
sys.exit();
else:
ai_agent_msg = \
'Naive AI, try to win it' \
if aiAlgo==0 else \
'Unbeatable minimax-AI, believe it or not, you cannot win absolutely!'
print('You will fight with: ', ai_agent_msg);
# Initialization.
gameOver = 0;
board = [' ',' ',' ',' ',' ',' ',' ',' ',' ',' '];
# Decide who, either human or AI, play first.
# 0: AI; 1: human.
print('Who play first? [0: AI; 1: human; 2: guess first]');
cmd = input()
if not cmd.isdigit():
whoseTurn = random.randint(0,1);
else:
if int(cmd)==0:
whoseTurn = 0
else:
whoseTurn = 1
while(not gameOver):
if whoseTurn == 0:
print('AI\'s turn')
if aiAlgo == 0:
nextMove = naiveAiNextMove(board);
else:
layer = 9 - board.count(' ')
nextMove, score = nextMove_complete_minimax(board,True,0,layer)
print('nextMove = {0}, score = {1}'.format(nextMove, score))
board[nextMove] = GAME_ROLE[0];
whoseTurn = 1;
else:
print('Human\'s turn')
isValid = 0;
while(not isValid):
isValid, nextMove = askHumanNextMove(board);
board[nextMove] = GAME_ROLE[1];
whoseTurn = 0;
drawBoard(board);
gameOver,winner = gameJudge(board);
gameRsltDisplay(winner);
4. 小结
以上实现的是一个完全minimax的算法,即每一步都执行minimax搜索到棋局结束,这样得到的全局最优解。这样的得到minimax-AI在Tic-Toe-Tac是不可战胜(unbeatable),无论是先手还是后手。但是由于Tic-Toe-Tac非常简单,如果对弈双方都是完美决策,则肯定会得到平局。所以,两个这样的AI对战总是会得到平局。
对于复杂一点的游戏,完全minimax搜索是不可行的。这时必须实现有限深度的搜索。接下来考虑面向有限深度minimax搜索的改造,以及进一步采用alpha-beta剪枝的方式来降低搜索复杂度以对付更为复杂的两人对战的游戏(零和对抗性博弈问题)。
2023-01-07 20:11 Correct a bug in gameJudge().
[Reference]
[1] 人工智能算法图解,清华大学出版社
[2] Minimax算法_PG-aholic的博客
[3] 最清晰易懂的MinMax算法和Alpha-Beta剪枝详解
[4] 极小化极大(Minimax)算法原理