C2-1.4(L1,L2)正则化
参考书籍

1 正则化的概念
- 正则化(Regularization) 是机器学习中对原始损失函数引入额外信息,以便防止过拟合和提高模型泛化性能的一类方法的统称。也就是目标函数变成了原始损失函数+额外项,常用的额外项一般有两种,中文称作L1正则化和L2正则化,或者L1范数和L2范数(实际是L2范数的平方)。
- L1正则化和L2正则化可以看做是损失函数的惩罚项。所谓惩罚是指对损失函数中的某些参数做一些限制。对于线性回归模型,使用L1正则化的模型叫做Lasso回归,使用L2正则化的模型叫做Ridge回归(岭回归)。
- 为什么只对W进行限制,而不对b进行限制呢?:
- 答:b是一个常数,影响拟合曲线的上下位移

回到顶部
2 正则化的作用
- L1正则化可以使得参数稀疏化,即得到的参数是一个稀疏矩阵,可以用于特征选择。
- 稀疏性,说白了就是模型的很多参数是0。通常机器学习中特征数量很多,例如文本处理时,如果将一个词组(term)作为一个特征,那么特征数量会达到上万个(bigram)。在预测或分类时,那么多特征显然难以选择,但是如果代入这些特征得到的模型是一个稀疏模型,很多参数是0,表示只有少数特征对这个模型有贡献,绝大部分特征是没有贡献的,即使去掉对模型也没有什么影响,此时我们就可以只关注系数是非零值的特征。这相当于对模型进行了一次特征选择,只留下一些比较重要的特征,提高模型的泛化能力,降低过拟合的可能。
- L2正则化可以防止模型过拟合(overfitting);一定程度上,L1也可以防止过拟合。
3、L1、L2正则化的公式表示
(把λ 变成 λ/2m )
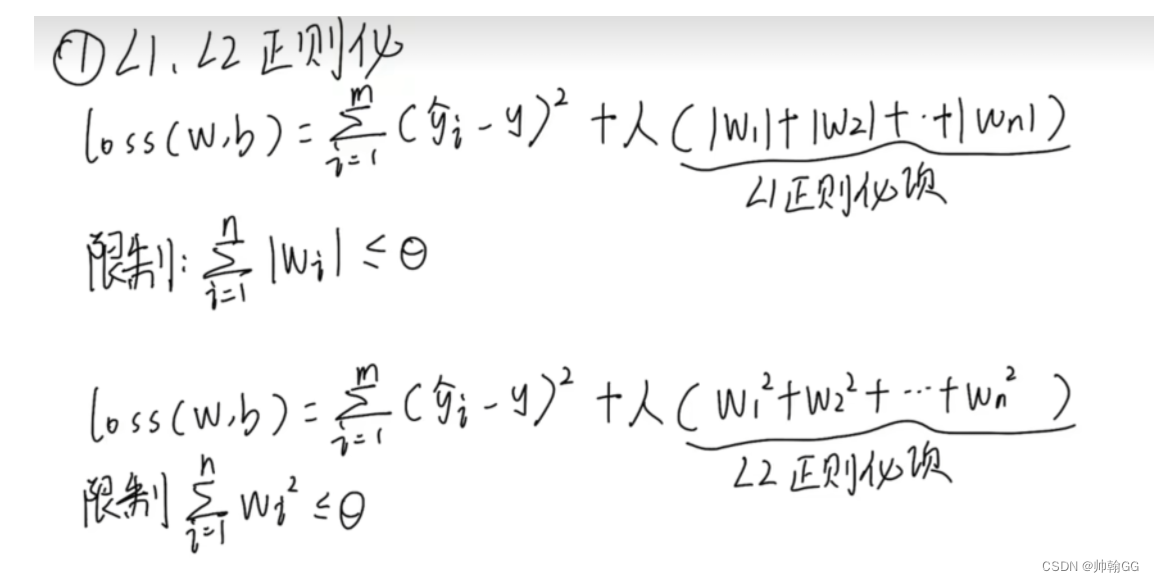
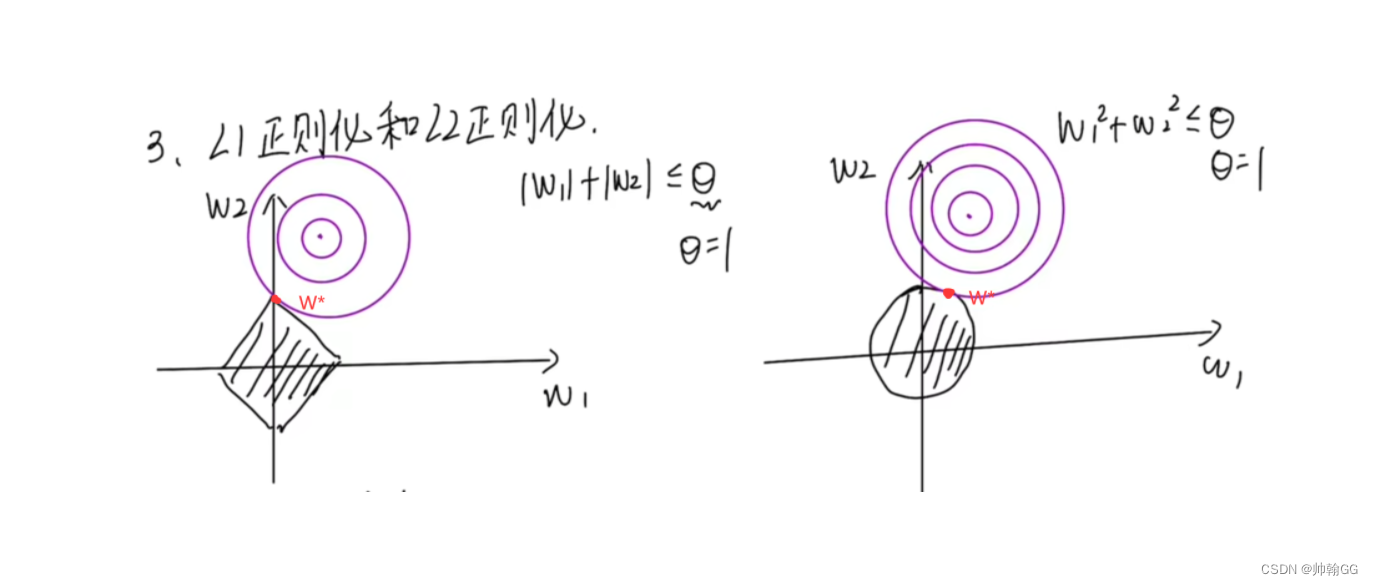
4、对L1正则化 ,L2正则化 可视化理解
- 黑色阴影:表示的是 w1 w2的限制条件的范围(W1,W2必须符合在阴影内)
- 紫色阴影:表示损失函数,每一圈代表的是LOSS的等高线、
- 要求:
- ①:W1,W2必须满足 <=Θ ,
- 且 ②:Loss需要在满足①条件之下,LOSS损失函数值最小
结论: 最后的结果是交点W*是最后正则化后W的结果
5、正则化如何降低过拟合
首先来复习一下**“正则化”公式:**
为了防止过拟合,线性回归的代价函数被叠加了一个正则化部分。如下图:
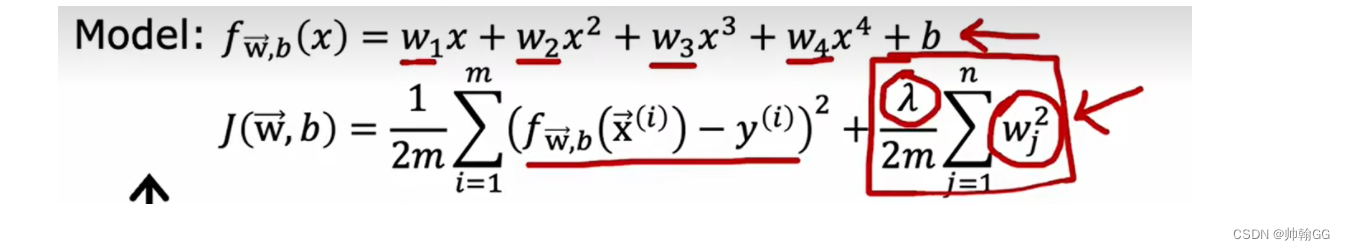
- 情况一/极端一:λ特别大时:
如λ取1000时,损失函数的值受正则化影响,为了减小J(w,b)最终的值,就尽量减少 w值,导致 W1 ≈W2≈…≈0
最终 f(x) ≈ b。最终造成了 欠拟合
- 情况二/极端二:λ特别小时:
如λ取0时,损失函数的值就导致了不受正则化的影响,就变成了以前那样的函数。形成了过拟合情况。
- 取中间值时候:

4.1、如何选择合适的lanmbda呢?
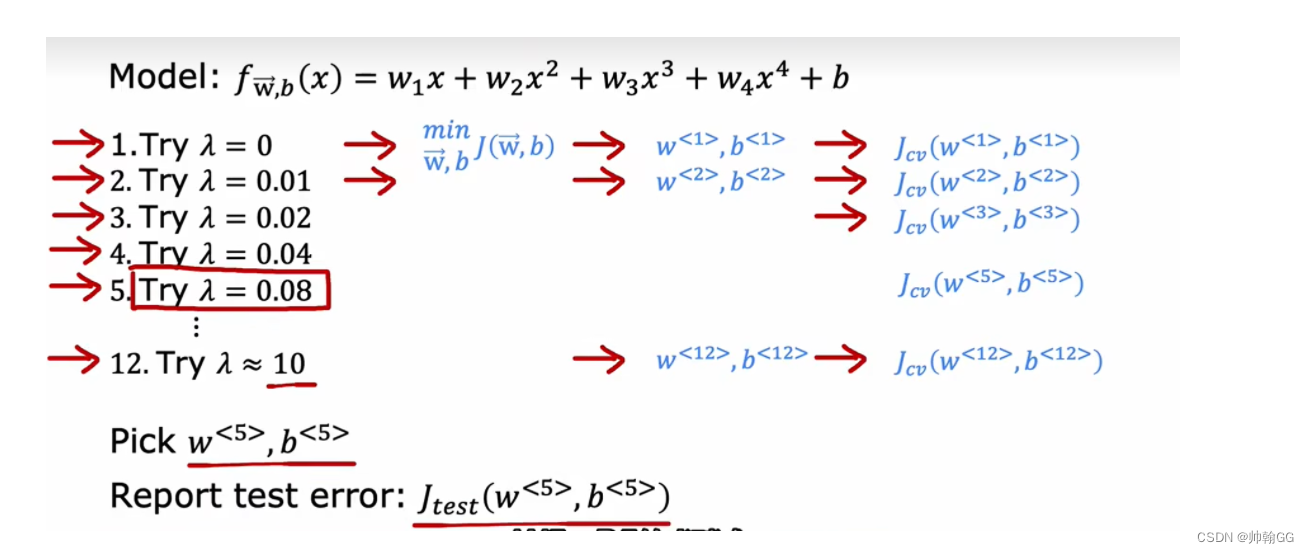
- Step1:使用训练集训练出12个不同程度的正则化模型,每个\lambda一个;
- Step2:使用12个模型分别对交叉验证集计算出验证误差;
- Step3:得出交叉验证误差最小的那个模型;(比如这里给出的 λ = 5的情况)
- Step4:使用Step3中得到的模型计算测试集上的误差,看是否能够推广。
4.2、lambda和偏差/方差的关系曲线
外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传