文章参考 Coursera吴恩达《神经网络与深度学习》课程笔记（4）-- 浅层神经网络

Shallow Neural Network

1、Neural Networks Overview

上周学过的逻辑回归可以作为神经网络其中的一个节点，神经网络要多一些隐藏层，下图为多了一层hidden layer 的情形。

这样从计算上来说，神经网络的正向传播和反向传播过程只是比逻辑回归多了一次重复的计算。正向传播过程分成两层，第一层是输入层到隐藏层，用上标[1]来表示：
$$z^{[1]}=W^{[1]}x+b^{[1]},a^{[1]}=\sigma (z^{[1]})$$
第二层是隐藏层到输出层，用上标[2]来表示：
$$z^{[2]}=W^{[2]}x+b^{[2]},a^{[2]}=\sigma (z^{[2]})$$
在写法上值得注意的是，方括号上标[i]表示当前所处的层数；圆括号上标(i)表示第i个样本。
反向传播同理，在计算dw，db时也要计算两次。

2、Neural Network Representation

下面我们以图示的方式来介绍单隐藏层的神经网络结构。如下图所示，单隐藏层神经网络就是典型的浅层（shallow）神经网络。

在结构上，从左到右，可以分成三层：输入层（Input layer），隐藏层（Hidden layer）和输出层（Output layer）。输入层和输出层，顾名思义，对应着训练样本的输入和输出，很好理解。隐藏层是抽象的非线性的中间层，这也是其被命名为隐藏层的原因。

在写法上，我们通常把输入矩阵X记为$a^{[0]}$，把隐藏层输出记为$a^{[1]}$，上标从0开始。下标用来表示第几个神经元，注意下标从1开始。例如$a_1^{[1]}$表示隐藏层第1个神经元，$a_1^{[1]}$表示隐藏层第2个神经元,，等等。这样，隐藏层有4个神经元就可以将其输出$a^{[1]}$写成矩阵的形式。

关于隐藏层对应的参数问题，$W^{[1]}$是（4,3），$b^{[1]}$是（4,1），$W^{[2]}$是（1,4），$b^{[2]}$是（1,1）。

这种单隐藏层神经网络也被称为两层神经网络（2 layer NN）。之所以叫两层神经网络是因为，通常我们只会计算隐藏层输出和输出层的输出，输入层是不用计算的。这也是我们把输入层层数上标记为0的原因。

3、Computing a Neural Network’s Output

对于单个神经元节点来说，他负责的功能如下所示，即完成 $z和a$的计算。

对于两层神经网络，就需要完成每一个神经元的计算

为了提高程序运算速度，我们引入向量化和矩阵运算的思想，将上述表达式转换成矩阵运算的形式 (注意在$Wx$过程中是利用$w$的的转置)：

即以下的四个式子：

4、Vectorizing Across Multiple Examples

上一部分我们只是介绍了单个样本的神经网络正向传播矩阵运算过程。而对于m个训练样本，我们也可以使用矩阵相乘的形式来提高计算效率。
我们需要把$x^{(i)}$依次计算出${\hat{y}}^{(i)}$

具体到每一个参数上就是：

我们先对x进行处理，
$$X=\left[\begin{array}{ccc}|& |& \dots \dots |\\ x^{(1)}& x^{(2)}& \dots \dots x^{(m)}\\ |& |& \dots \dots |\end{array}\right]$$
之后利用$Z^{[1]}=W^{[1]}X+b^{[1]}$得到：
$$Z^{[1]}=\left[\begin{array}{ccc}|& |& \dots \dots |\\ z^{[1](1)}& z^{[1](2)}& \dots \dots z^{[1](3)}\\ |& |& \dots \dots |\end{array}\right]$$
然后$A^{[1]}=\sigma (Z^{[1]})$
$$A^{[1]}=\left[\begin{array}{ccc}|& |& \dots \dots |\\ a^{[1](1)}& a^{[1](2)}& \dots \dots a^{[1](3)}\\ |& |& \dots \dots |\end{array}\right]$$
之后$Z^{[2]}=W^{[2]}{A}^{[1]}+b^{[2]},A^{[2]}=\sigma (Z^{[2]})$

5、Explanation for Vectorized Implementation

Andrew又手写了一下上一节公式的分量化具体推导

6、Activation Functions

首先我们来比较sigmoid函数和tanh函数。对于隐藏层的激活函数，一般来说，tanh函数要比sigmoid函数表现更好一些。因为tanh函数的取值范围在[-1,+1]之间，隐藏层的输出被限定在[-1,+1]之间，可以看成是在0值附近分布，均值为0。这样从隐藏层到输出层，数据起到了归一化（均值为0）的效果。因此，隐藏层的激活函数，tanh比sigmoid更好一些。而对于输出层的激活函数，因为二分类问题的输出取值为{0,+1}，所以一般会选择sigmoid作为激活函数（但是只有二分类问题的输出层用sigmoid，其他一律用tanh更好）。

观察sigmoid函数和tanh函数，我们发现有这样一个问题，就是当|z|很大的时候，激活函数的斜率（梯度）很小。因此，在这个区域内，梯度下降算法会运行得比较慢。在实际应用中，应尽量避免使z落在这个区域，使|z|尽可能限定在零值附近，从而提高梯度下降算法运算速度。

为了弥补sigmoid函数和tanh函数的这个缺陷，就出现了ReLU激活函数。ReLU激活函数在z大于零时梯度始终为1；在z小于零时梯度始终为0；z等于零时的梯度可以当成1也可以当成0，实际应用中并不影响。对于隐藏层，选择ReLU作为激活函数能够保证z大于零时梯度始终为1，从而提高神经网络梯度下降算法运算速度。但当z小于零时，存在梯度为0的缺点，实际应用中，这个缺点影响不是很大。为了弥补这个缺点，出现了Leaky ReLU激活函数，能够保证z小于零是梯度不为0。

最后总结一下，如果是分类问题，输出层的激活函数一般会选择sigmoid函数。但是隐藏层的激活函数通常不会选择sigmoid函数，tanh函数的表现会比sigmoid函数好一些。实际应用中，通常会会选择使用ReLU或者Leaky ReLU函数，保证梯度下降速度不会太小。其实，具体选择哪个函数作为激活函数没有一个固定的准确的答案，应该要根据具体实际问题进行验证（validation）。

7、Why do you need Non-Linear Activation Functions?

经过推导我们发现仍是输入变量x的线性组合。这表明，使用神经网络与直接使用线性模型的效果并没有什么两样。即便是包含多层隐藏层的神经网络，如果使用线性函数作为激活函数，最终的输出仍然是输入x的线性模型。这样的话神经网络就没有任何作用了。因此，隐藏层的激活函数必须要是非线性的。

另外，如果所有的隐藏层全部使用线性激活函数，只有输出层使用非线性激活函数，那么整个神经网络的结构就类似于一个简单的逻辑回归模型，而失去了神经网络模型本身的优势和价值。

8、Derivatives of activation functions

1. $$g(z)=\frac{1}{1+e^{-z}}$$
   $$\frac{d}{dz}g(z)=g(z)(1-g(z))=a(1-a)$$
2. $$g(z)=tanh(z)=\frac{e^z-e^{-z}}{e^z+e^{-z}}$$
   $$\frac{d}{dz}g(z)=1-(g(z){)}^2$$
3. $$g(z)=max(0,z)$$
   $$g^{{}^{\prime }}(z)=\{\begin{array}{l}0,z<0\\ 1,z\ge 0\end{array}$$
4. $$g(z)=max(0.01z,z)$$
   $$g^{{}^{\prime }}(z)=\{\begin{array}{l}0.01,z<0\\ 1,z\ge 0\end{array}$$

9、Gradient descent for neural networks

由于涉及到两层网络，反向传播计算要比逻辑回归更复杂，对于单个样本和m个样本的总结如下（最后一层按照sigmoid来用）：

Notice:计算$d{Z}^{[1]}$用的*不是矩阵乘法，是元素乘法

    # X(2,400),Y(1,400)
    dZ2 = A2 - Y
    dW2 = np.dot(dZ2,A1.T) / m  # (1,4)
    db2 = np.sum(dZ2,axis=1,keepdims = True) / m # (1,1)
    dZ1 = np.dot(W2.T,dZ2)*(1 - np.power(A1, 2)) #(4,400)*(4,400)
    dW1 = np.dot(dZ1,X.T)/m
    db1 = np.sum(dZ1,axis=1,keepdims = True) / m

10、Backpropagation intuition(optional)

使用computation graph进行的具体推导，看总结的公式即可。

11、Random Initialization

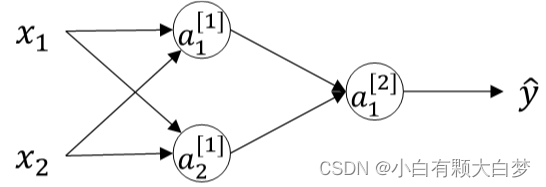
对于这样一个网络，如果把参数全部初始化为0：
$$W^{[1]}=\left[\begin{array}{cc}0& 0\\ 0& 0\end{array}\right]$$
$$W^{[2]}=\left[\begin{array}{cc}0& 0\end{array}\right]$$
这样使得隐藏层第一个神经元的输出等于第二个神经元的输出,因此，这样的结果是隐藏层两个神经元对应的权重行向量和每次迭代更新都会得到完全相同的结果，完全对称。这样隐藏层设置多个神经元就没有任何意义了。
解决方法：

W_1 = np.random.randn((2,2))*0.01
b_1 = np.zero((2,1))
W_2 = np.random.randn((1,2))*0.01
b_2 = 0

这里我们将和乘以0.01的目的是尽量使得权重W初始化比较小的值。之所以让W比较小，是因为如果使用sigmoid函数或者tanh函数作为激活函数的话，W比较小，得到的|z|也比较小（靠近零点），而零点区域的梯度比较大，这样能大大提高梯度下降算法的更新速度，尽快找到全局最优解。如果W较大，得到的|z|也比较大，附近曲线平缓，梯度较小，训练过程会慢很多。

当然，如果激活函数是ReLU或者Leaky ReLU函数，则不需要考虑这个问题。但是，如果输出层是sigmoid函数，则对应的权重W最好初始化到比较小的值。

12、Quiz

1. 
   搞混了，tanh在x=0处的导数是确定的，为1，在0处不可导的是relu，人为设置即可，一般设为0.

13、LAB

Reminder: The general methodology to build a Neural Network is to:

1. Define the neural network structure ( # of input units, # of hidden units, etc).
2. Initialize the model’s parameters
3. Loop:
   • Implement forward propagation
   • Compute loss
   • Implement backward propagation to get the gradients
   • Update parameters (gradient descent)

In practice, you’ll often build helper functions to compute steps 1-3, then merge them into one function called nn_model(). Once you’ve built nn_model() and learned the right parameters, you can make predictions on new data.

最终版本：（按照如下方式拆分函数）

# GRADED FUNCTION: nn_model

def nn_model(X, Y, n_h, num_iterations = 10000, print_cost=False):
    """
    Arguments:
    X -- dataset of shape (2, number of examples)
    Y -- labels of shape (1, number of examples)
    n_h -- size of the hidden layer
    num_iterations -- Number of iterations in gradient descent loop
    print_cost -- if True, print the cost every 1000 iterations
    
    Returns:
    parameters -- parameters learnt by the model. They can then be used to predict.
    """
    
    np.random.seed(3)
    n_x = layer_sizes(X, Y)[0]
    n_y = layer_sizes(X, Y)[2]
    
    # Initialize parameters
    #(≈ 1 line of code)
    # parameters = ...
    # YOUR CODE STARTS HERE
    parameters = initialize_parameters(n_x, n_h, n_y)
    # YOUR CODE ENDS HERE
    
    # Loop (gradient descent)

    for i in range(0, num_iterations):
         
        #(≈ 4 lines of code)
        # Forward propagation. Inputs: "X, parameters". Outputs: "A2, cache".
        # A2, cache = ...
        
        # Cost function. Inputs: "A2, Y". Outputs: "cost".
        # cost = ...
 
        # Backpropagation. Inputs: "parameters, cache, X, Y". Outputs: "grads".
        # grads = ...
 
        # Gradient descent parameter update. Inputs: "parameters, grads". Outputs: "parameters".
        # parameters = ...
        
        # YOUR CODE STARTS HERE
        A2, cache = forward_propagation(X, parameters)
        cost = compute_cost(A2, Y)
        grads = backward_propagation(parameters, cache, X, Y)
        parameters = update_parameters(parameters, grads)
        # YOUR CODE ENDS HERE
        
        # Print the cost every 1000 iterations
        if print_cost and i % 1000 == 0:
            print ("Cost after iteration %i: %f" %(i, cost))

    return parameters