RMQ问题

RMQ（Range Minimum/Maximum Query）问题，又叫做区间最值问题，即对于长度为n的数列A，回答若干询问RMQ(A,i,j)(i,j<=n)，返回数列A中下标在i,j里的最小(大）值。

问题引入

给你一个序列： [4,6,9,8,7,6,3,1,2,4]，输入一个left和一个right，表示在 [left，right]这段这个范围的最值是多少？我们假定数组的下标从1开始，数组的下标范围：[1,10]
例如：
left=1 right=5 : [4,6,9,8,7] 最大值是 9，最小值是4
left=4，right=6 : [8,7,6] 最大值是8，最小值是6

我们如何求解这样的问题呢？

暴力解法容易想出来，我们只需要 打擂台算法便可以求出这个区间的最值，打擂台算法指的是从区间的开始下标处取得 nums[left]当作第一个元素，记作num，然后依次与[left, right]内的元素进行比较，要得到最大值，则当后面的元素比num大时，更新num；要取得最小值则反之。

for (int i=left;i<right;i++) //假定left，right满足下标范围
{
	//取最大值
	if (numMax<nums[i]) numMax=nums[i];
	else if (numMin>nums[i]) numMin=nums[i];
}

这个算法，我们每次都需要枚举每一个范围内的元素，进而更新得到合适的值，但是它的时间复杂度呢？
假设我们需要 询问m次，每次询问都需要一个left和right，然后分别球的每一次询问的过程中的最大值，很显然，我们需要外层再套一个循环，表示询问每一次，然后再执行打擂台，那么就是这样的：

for (int j=0;j<m;j++)
{
	for (int i=left;i<right;i++) //假定left，right满足下标范围
	{
		//取最大值
		if (numMax<nums[i]) numMax=nums[i];
		else if (numMin>nums[i]) numMin=nums[i];
	}
}

m表示询问的次数，n表示某一区间的范围，则可以得到算法的时间复杂度 O（mn），它的效率是非常低的。

有没有什么办法可以改善在区间中查询最大（小）值的算法呢？

---

ST算法

ST算法是求解RMQ问题的优秀算法，它适用于静态空间的RMQ查询。就类似于刚才我们所引入的那个问题，就是静态空间的RMQ。

---

ST算法的原理：
我们可以把整个区间分成多个子区间，假设我们通过某种方法之前提前知道了这两个子区间的最值，则很轻松，我们可以立马得知整个区间的最小值。

但是这样做我们必须首先基于以下的事实： 整个大区间必须被两个子区间所覆盖，相当于两个子区间的并集必须就是整个区间，两个子区间的范围可以覆盖，所以我们才能得到上述的结论。

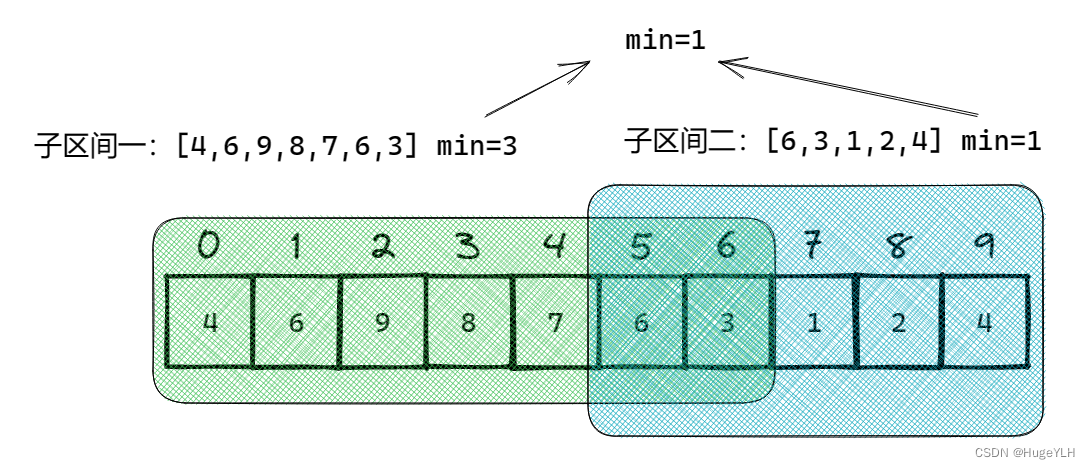
这便是ST算法的基本思想：

1. 我们把整个区间划分为合适的子区间，然后求得子区间的最值。
2. 对于任意一个区间的最值查询，我们都可以转换为求覆盖了它的两个子区间的最值，利用这两个子区间的最值求得这个任意区间的最值。

---

那么我们明白了，想要求某个区间的最值，转换为两个子区间的最值，然后直接把他们的最值进行比较就得到了需要求得区间的最值。 我们可以利用这个方法求得任意区间的最值，所以我们面临一个问题，我们该如何划分这个数组呢，才能使得任意一个区间我们都可以得到子区间的最值。

划分数组成子数组的方式：利用倍增的思想。

---

倍增

倍增顾名思义： 成倍增加。 其实它与另一个我们所熟知的算法成一个对立的关系：二分查找

二分查找：不断缩小区间，直到得到了符合条件的最小的区间，得到结果。
倍增：不断增大区间，直到某一个条件。。。

二分查找算法在大多数问题中的时间复杂度是O（nlog2^n）
倍增思想在大多数问题中的时间复杂度也是O（nlog2^n）

我们再来思考这样一个问题：倍增难道就是简单的每次区间长度扩大二倍吗？ 不是的，难道二分查找就是每次把区间缩小二倍？很显然不是，二分查找的缩小性与 log2^ n有关，我们可以得到每次二分都会缩小 log2^n倍，所以我们的倍增就可以理解为每次增大log2 ^n倍。

倍增：1 -> 2 -> 4 -> 8 -> 16 … -> 2^k ，假如我们所要求的数是16，那么我们从1总共需要倍增4次， k = log2 ^ n n=2 ^ k k=4

---

我们的区间也可以按照这种方式来划分，每次划分 2 ^ k 个长度的范围，k从0开始：

• 总共有 k = log2 ^ n 组，其中 n = 10（区间的总长度），所以向下取整组数： k = 3 k从0 开始，闭区间 [0,3] 。
• 每组划分的子区间长度是 2 ^ k，每组可以划分的最多块数： (n - 2^ k +1)
• 第一组：k = 0 每块长度为2^0 = 1，划分10（n - 2 ^ 0 + 1）块。
• 第二组：k =1 每块长度为2^1 =2，划分9（n - 2 ^ 1 + 1）块。
• 第三组：k =2 每块长度为2^2 =4，划分7（n - 2 ^ 2 + 1）块。
• 第四组：k =3 每块长度为2^3 =8，划分3（n - 2 ^ 3 + 1）块。
  
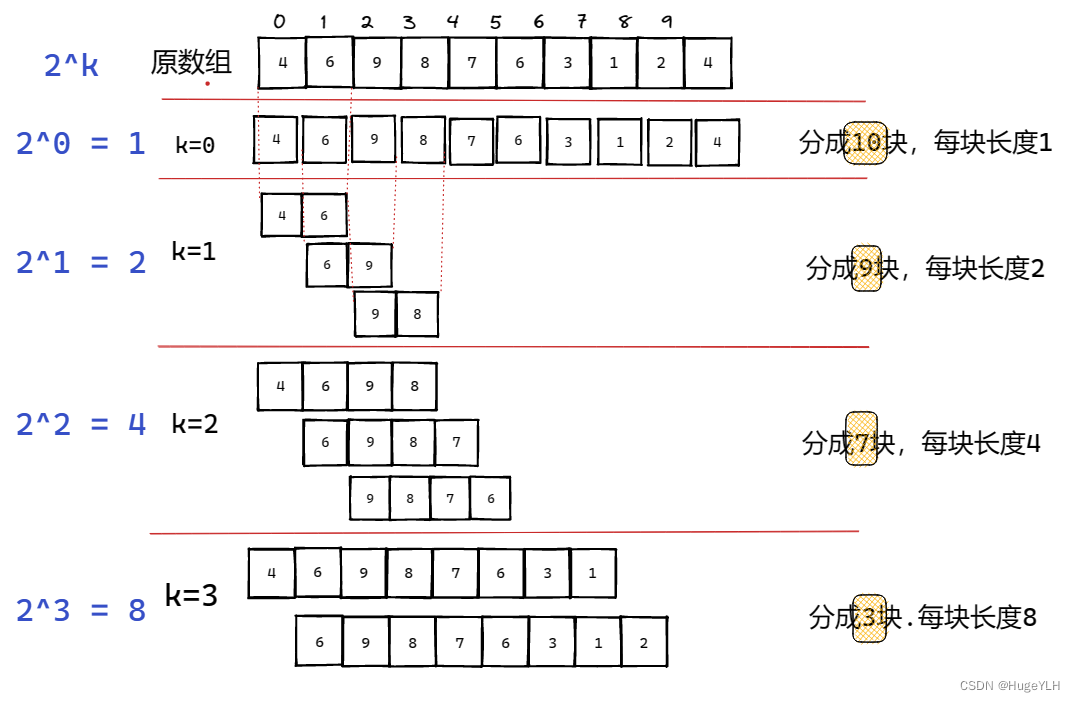
  这时我们便可以发现，每组每块区间的最值都可以由前一组递推而来：
• k = 1 ：第一块：元素[4,6]的最小值是 4，由上一组（k=0）的前两块[4],[6]的最小值得到。
• k = 2：第一块：元素[4,6,9,8]的最小值是4，由上一组（k=1）的第一块[ 4,6 ]和第三块[ 9,8 ]得到，而这两小块又可以通过第一步（k=1时）由k=0的对应的位置两小块得到。
• k = 3：第一块：元素 [4,6,9,8,7,6,3,1]的最小值是1，由上一组（k=2）的第一块[4,6,9,8]和第四块(图中未画出)[7,6,3,1]得到，同样这两个子块，我们之前肯定已经求过了。

这样看，我们似乎得到了一个动态规划的过程：求解当前问题，可以转换为n个子问题，然后由子问题的答案得到当前答案的最优解。

---

我们创建dp二维数组，规定：

• s：（start）表示 每组中每一块的起始位置（下标0开始）
• k：k标识组，进而得到每一组的每一块的区间长度： 2 ^ k
• dp[s][kl] ：表示左端点为 s，区间长度为 2 ^ k的区间的最值。

---

我们可以推导出这个动态规划的递推公式：

这个dp公式咋这么复杂啊，还是有 s+ 2^(k-1) 是啥意思啊，我们接下来就来一步一步推导出这个dp公式。

---

ST递推公式

1. 首先我们得知，第一组 k=0时，随着起始点s的变化，每块子区间的长度总是0，因此dp[0][0]，dp[1][0]，dp[2][0]，dp[3][0]…dp[n-1][0]分别表示起始点是0，1，2，3…一直到n-1最后一个元素，有10块，每块子区间的长度是0，所以每块子区间的最小值一定是这个位置的元素本身。
   

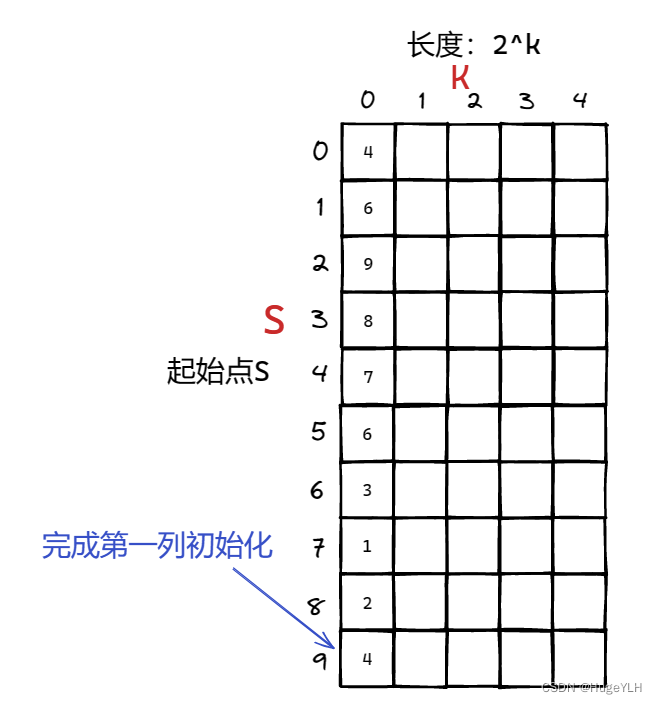
2. 第二组：k = 1 时，每块子区间的区间长度是2，因此dp[0][1] 表示起始点0，区间长度是2的子区间的最小值是（由上一组推出，刚才已经说过了，min(4,6)=4）；dp[1][1]表示起始点1，区间长度是2的子区间的最小值是（min(6,9)=6），同理可以画出第二组的图像：

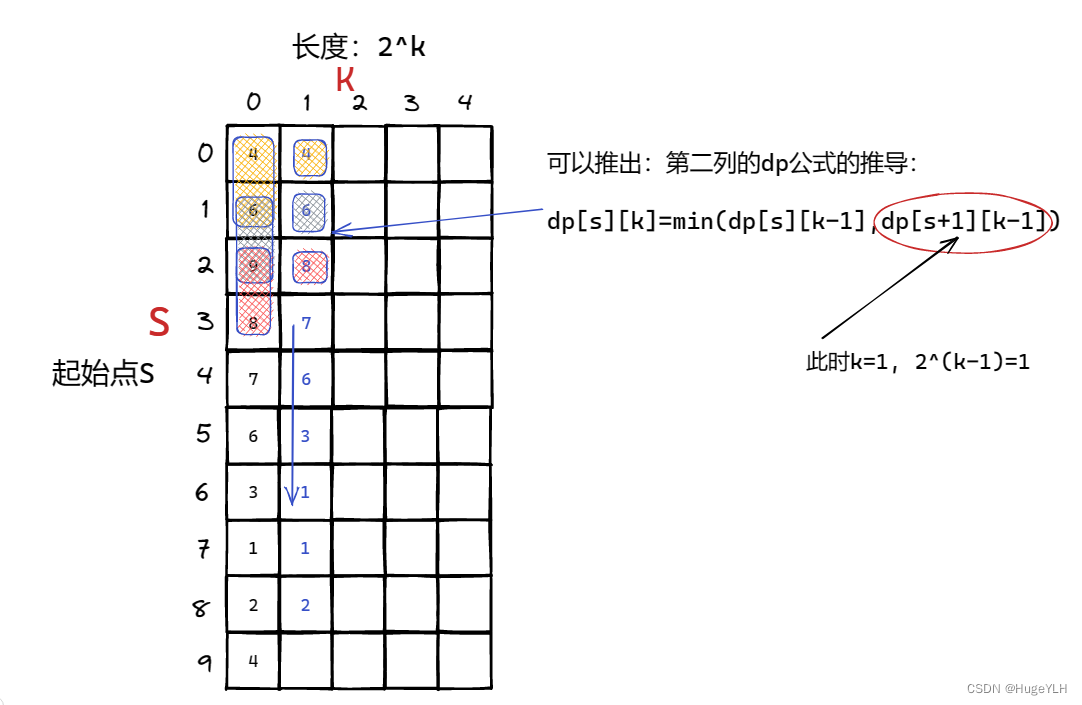
3. 第三组：k = 2 时，每块子区间的区间长度是4（2 ^ 2），因此dp[0][2] 表示起始点0，区间长度是4的子区间的最小值是（由前一组推出，min([4,6],[9,8])=4）；dp[1][2]表示起始点1，区间长度是4的子区间的最小值是（min([6,9],[8,7])=6），同理可以画出第三组的图像：

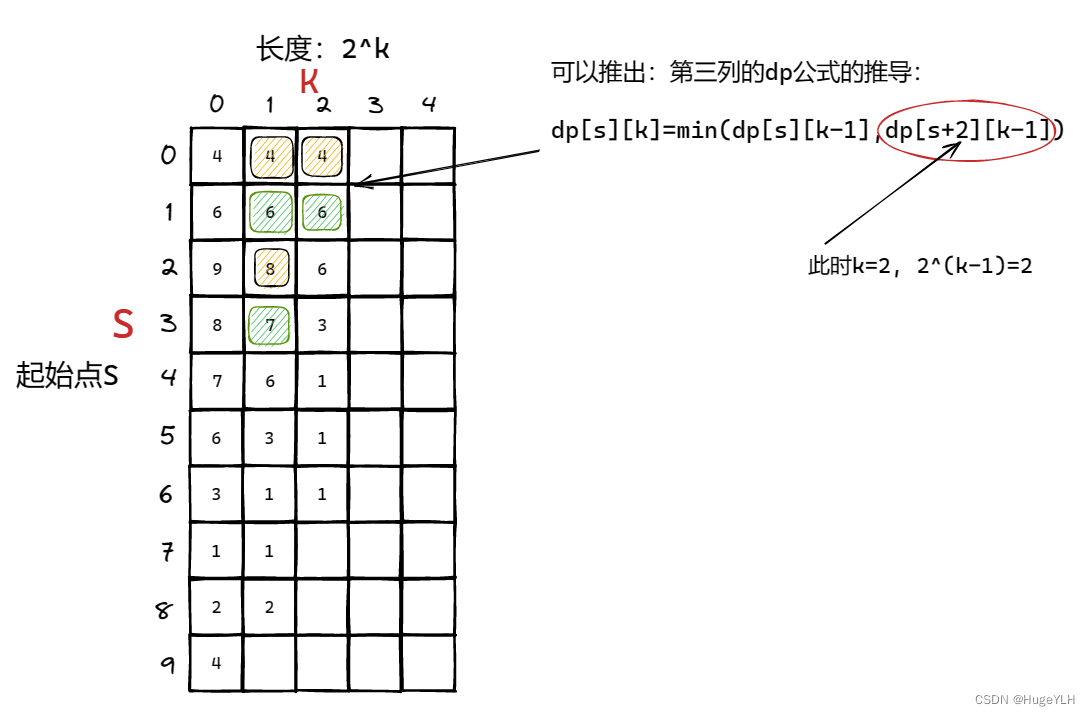
4. 第四组：k = 3 时，每块子区间的区间长度是8（2 ^ 3），因此dp[0][3] 表示起始点0，区间长度是8的子区间的最小值是（由前一组推出，min([4,6,9,8],[7,6,3,1])=1）；dp[1][3]表示起始点1，区间长度是8的子区间的最小值是（min([6,9,8,7],[6,3,1,2])=1），同理可以画出第四组的图像：

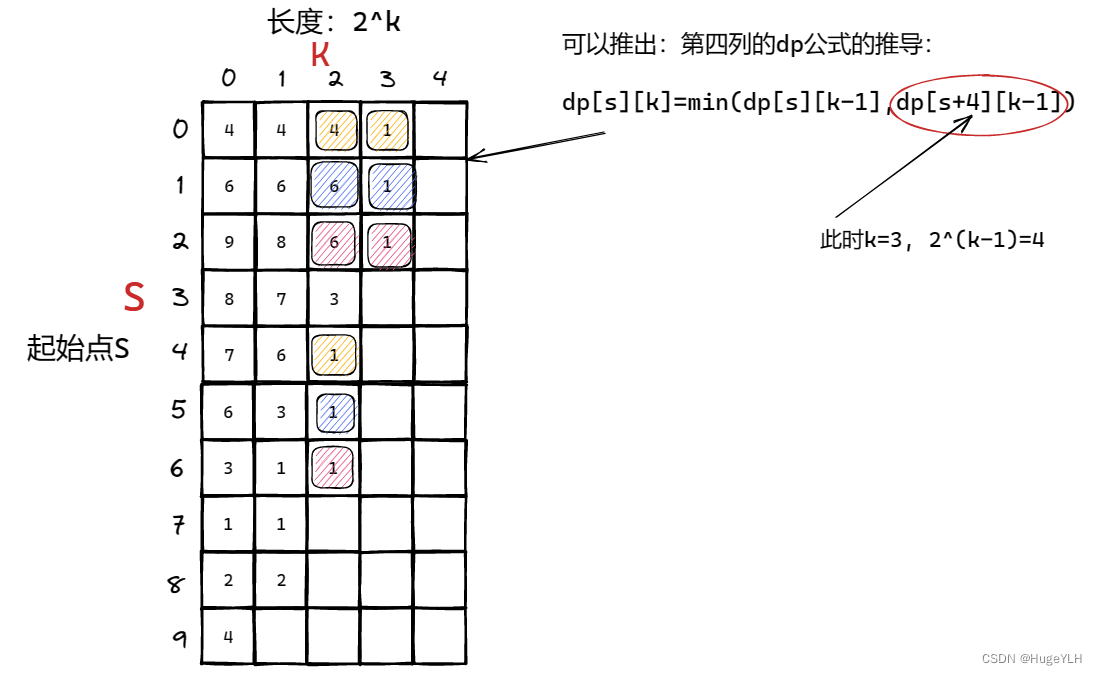
k 属于 [0,3],所以遍历结束到结束，

可以看到：

• 当我们填充每一列的时候，随着 k 的不同，我们的dp公式略有不同，因为k代表了每一块子区间的长度，为 2^k，所以我们由 前一个k组推出当前k的方式也略有不同，综上：我们的dp公式如下所示：

---

查询任意区间的最值

对于需要查询的任意一个区间 [L,R]，它的起始点是L，终点是R（规定L<=R）,这些区间的交集就是 [L,R]。

求任意区间最值的方法：

刚才我们已经划分了每一组每一块子区间，现在我们就可以认为：以L为起点的区间，它的后面包含有长度 1 ，2，4，8… 的子区间，以R为终点，它的前面也包含有 1，2，4，8…的子区间。我们可以把需要查询的区间分成任意的两个等长的子区间，这两个子区间的起点和终点分别是L和R，并且两个子区间一定覆盖（交集）需查询区间， 区间最值便可以由这两个小区间的最值得到，时间复杂度是O（1）

看图：

当我们需要查询的区间L=4，R=9的时候：即需要求dp[4][k]的值即可，注意这个k不是图中的k=3，这个k表示的含义是区间长度是 2 ^ k 的区间。根据我们上面分析求任意区间的最值的方法，我们需要把 [L,R]这一区间分成两块长度为 k 的子区间，但是这个 k 如何确定呢？

---

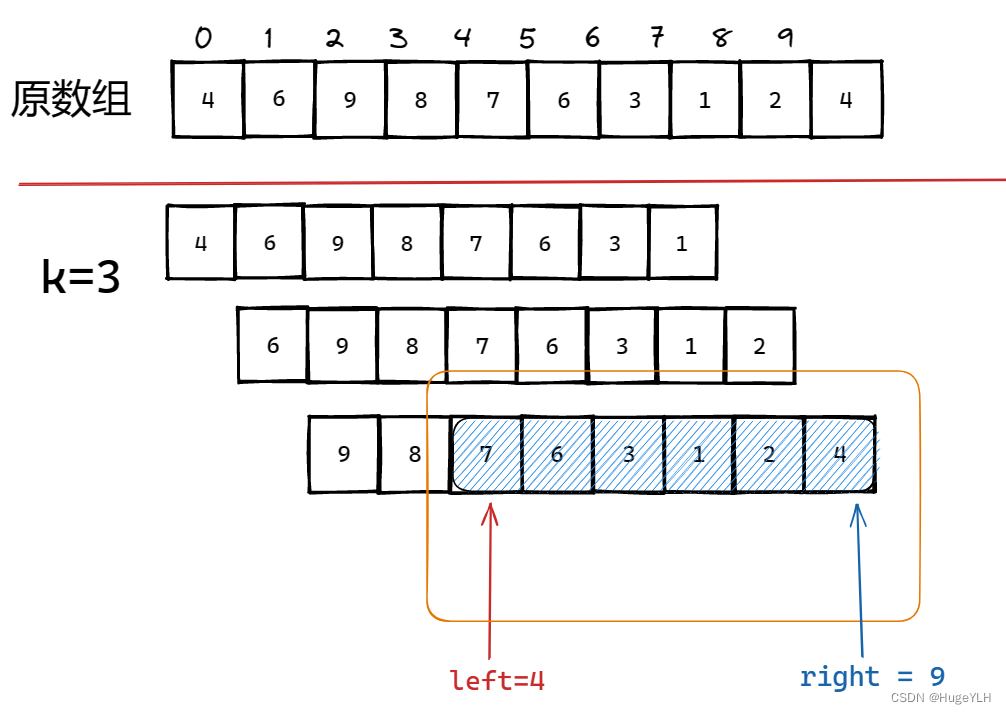
如何确定 k ？

1. 首先我们可以根据 L 和 R求出这块区间的长度：len = R-L+1，得到了长度之后，我们可以知道： 2 ^ k< len <= 2^(k+1) ，即总长度len一定大于划分的两块子区间的长度，并且这两个子区间的长度一定要取得最大值。我们把数据先带入求k，可以得到 k=2，k=2就是两个子区间的长度：2^k =4，所以求k的方法：k= log2(len)
2. 两块子区间的长度是2^k，并且还需要满足两个子区间分别位于 L 和 R上，需要覆盖整个子区间，因此这两个子区间的划分如图所示。
3. 我们只需要求出这两个子区间[L，L+4] 和 [R -(2^k)+1，R]的最值，就可以得到 [L，R]区间的最值。
4. 所以求任意区间的最值的公式：
   
   

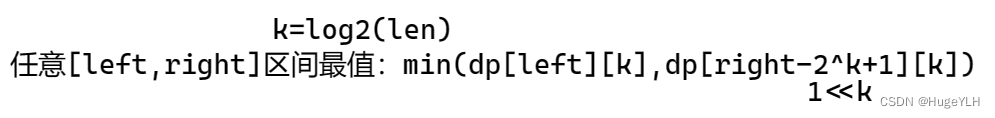
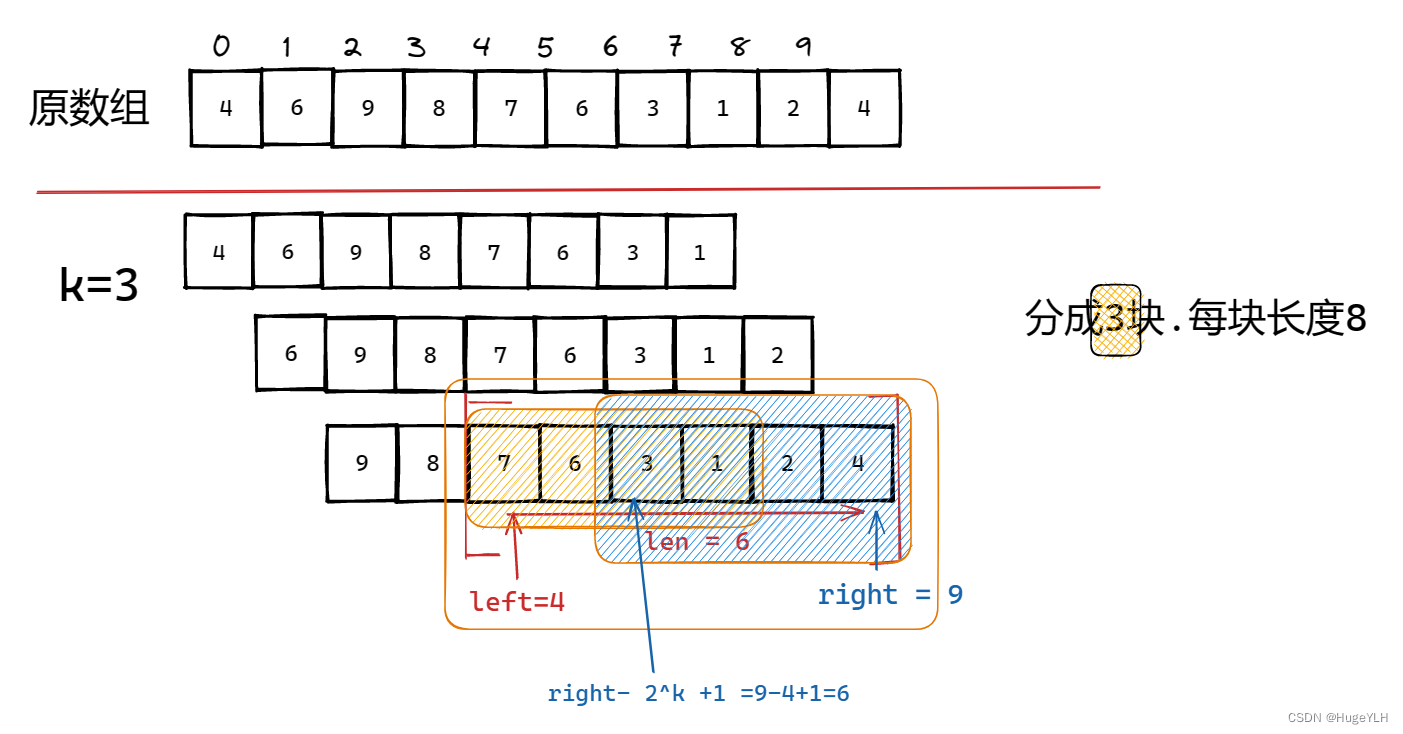
auto getnum = [=](int left, int right)
{
	int k = log2(right - left + 1);
	return max(dp[left][k], dp[right - (1 << k) + 1][k]);
};

代码实现

所以我们的ST求解某一个区间的最值就已经完成了，有了dp这个数组，我们就可以做到在 O（1） 时间里找到 起始点为left，终点为right的 子区间的最值，因为我们每一个子区间的最值早已记录在dp数组里了。

请注意：我们让区间的下标从1开始 [1,n]，这样做是为了在做题时方便，当然从0开始也可以，这时我们在init_dp的时候，s就要从0开始，并且s < n - (1 << k) + 1，由于很多OJ题目都是从1开始的，所以最后我们在求getnum的时候，需要L-1，R-1，当然我们可以直接让下标从1开始就可以了。

求区间最小值：min，求最大值直接把min换为max即可。

namespace test25
{
	int n, m;
	constexpr int maxnum = 500005;
	vector<int> vec(maxnum);
	//dp数组：行数表示s，列数表示k，假定k能够表示足够大的数字(2^k)
	vector<vector<int>> dp(maxnum, vector<int>(40));
	void init_dp()
	{
		//第一组：区间长度是1的初始化
		for (int s = 1; s <= n; s++)
		{
			dp[s][0] = vec[s];
		}
		//求出最大能容纳多少组
		int p = log2(n);
		//对于每一组：1,2,3 ... p
		for (int k = 1; k <= p; k++)
		{
			//求出s为 1,2,3...n-1的对应的每个区间的最值
			for (int s = 1; s <= n - (1 << k) + 1; s++)
			{
				dp[s][k] = min(dp[s][k - 1], dp[s + (1 << (k - 1))][k - 1]);
			}
		}
	}
	int getnum(int L, int R)
	{
		int len = R - L + 1;		//需查询区间长度
		int k = log2(len);		//划分成两个子区间，子区间的最大长度
		return min(dp[L][k], dp[R - (1 << k) + 1][k]);
	}
	void test()
	{
		//n表示区间的长度，m表示询问的次数
		cin >> n >> m;	
		
		for (int i = 1; i <= n; i++)
		{
			scanf("%d", &vec[i]);
		}
		init_dp();
		//打印，查询结果正确性
		/*int p = log2(n);
		for (int s = 1; s <= n; s++)
		{
			for (int k = 0; k <= p; k++)
			{
				cout << dp[s][k] << " ";
			}
			cout << endl;
		}*/
		//对于每一次询问
		for (int i = 0; i < m; i++)
		{
			int L, R;
			scanf("%d%d", &L, &R);
			printf("%d\n", getnum(L, R));
		}
	}
}

打印结果如下：

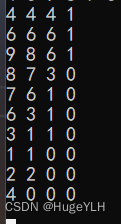
这与我们上面自己推导出来的dp数组的值完全一样，不信你对比一下。

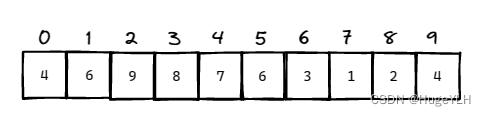
L = 1，R = 5 内的最小值是4
L= 2，R = 6内的最小值是6