题目链接:
二叉树的最大深度 https://leetcode.cn/problems/maximum-depth-of-binary-tree/submissions/
二叉树的最小深度 https://leetcode.cn/problems/minimum-depth-of-binary-tree/
平衡二叉树 https://leetcode.cn/problems/balanced-binary-tree
1.二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
输入: [3,9,20,null,null,15,7]
3
/ \
9 20
/ \
15 7
输出: 3
1.1 深度优先搜索
分析:使用递归,不断找出每个节点左子树和右子树的最大深度,取较大者,每轮递归深度加一
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
elif not root.left and not root.right:
return 1
else:
return max(self.maxDepth(root.left),self.maxDepth(root.right)) + 11.2 广度优先搜索
分析:层序遍历二叉树,结束一层并存好下一层(如果有)的节点后,深度加一
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
q = [root]
height = 0
while q:
currentSize = len(q)
for i in range(currentSize):
node = q.pop(0)
if node.left:
q.append(node.left)
if node.right:
q.append(node.right)
height += 1
return height2.二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
示例 :
输入:root = [3,9,20,null,null,15,7]
3
/ \
9 20
/ \
15 7
输出:2
2.1 深度优先搜索
分析:使用递归,不断找出每个节点左子树和右子树的最小深度,取较小者,每轮递归深度加一
如果直接比较左右子树高度,注意排除左右子树高度为0,即不存在的情况,例如以下这种树
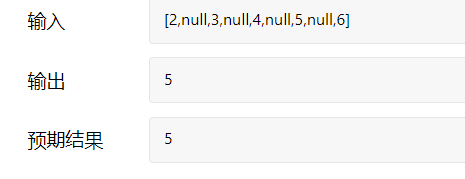
class Solution:
def minDepth(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
elif not root.left and not root.right:
return 1
else:
depthL = self.minDepth(root.left)
depthR = self.minDepth(root.right)
return min(depthL,depthR) + 1 if min(depthL,depthR) != 0 else max(depthL,depthR) + 1
如果依次判断左右子节点是否存在,然后取较小者,初始可以设置一个大数作为比较基准
class Solution:
def minDepth(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
elif not root.left and not root.right:
return 1
else:
minDepth = 10**9
if root.left:
minDepth = min(self.minDepth(root.left),minDepth)
if root.right:
minDepth = min(self.minDepth(root.right),minDepth)
return minDepth + 12.2 广度优先搜索
分析:层序遍历二叉树,如果当前层的节点没有左右子节点,说明它是叶子节点,停下来,返回该层的深度;否则,结束一层并存好下一层(如果有)的节点后,深度加一
class Solution:
def minDepth(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
q = [root]
height = 0
#判断左右子树是否存在
existL = 0
existR = 0
while q:
currentSize = len(q)
for i in range(currentSize):
node = q.pop(0)
if node.left:
q.append(node.left)
if node.right:
q.append(node.right)
if not node.left and not node.right:
return height+1
height += 1
return height3. 平衡二叉树
给定一个二叉树,判断它是否是高度平衡的二叉树。本题中,一棵高度平衡二叉树定义为:一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
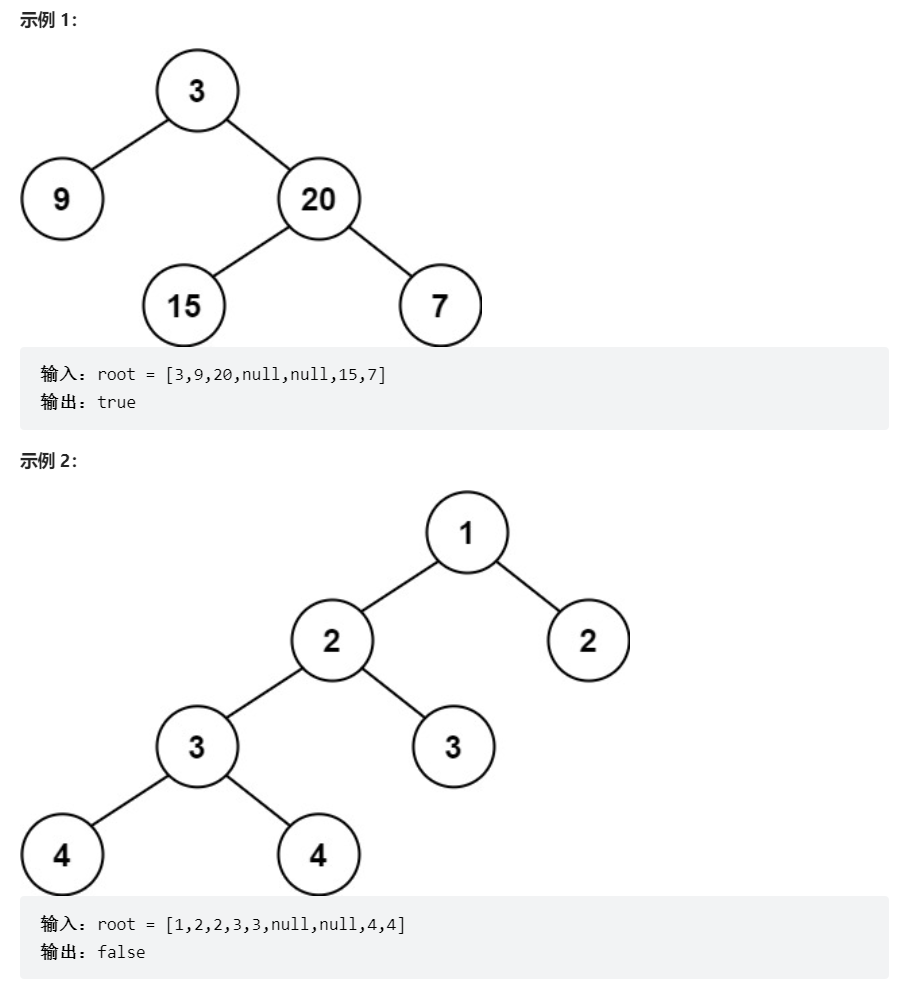
3.1 自顶向下递归
自顶向下地递归地判断左子树和右子树的深度差,一旦大于1就返回False
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
depth = 0
if not root:
return 0
elif not root.left and not root.right:
return 1
else:
return max(self.maxDepth(root.left),self.maxDepth(root.right)) + 1
def isBalanced(self, root: Optional[TreeNode]) -> bool:
if not root:
return True
elif not root.left and not root.right:
return True
else:
depthL = self.maxDepth(root.left)
depthR = self.maxDepth(root.right)
if abs(depthL-depthR) > 1:
return False
else:
return self.isBalanced(root.left) and self.isBalanced(root.right)3.2 自底向上递归
用列表设置一个标志(也可以使用global或nonlocal),初始为True,代表是否平衡二叉树
在找最大深度的过程中判断左子树和右子树的深度差是否大于1,大于1则不平衡返回-1同时修改标志
class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
flag = [True]
def maxDepth(root):
if not root:
return 0
depthL = maxDepth(root.left)
depthR = maxDepth(root.right)
deltaDepth = abs(depthL-depthR)
if deltaDepth > 1:
flag[0] = False
return -1
return max(depthL,depthR) + 1
maxDepth(root)
return flag[0]