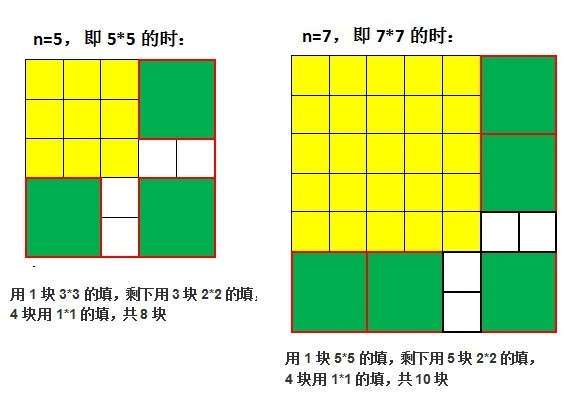
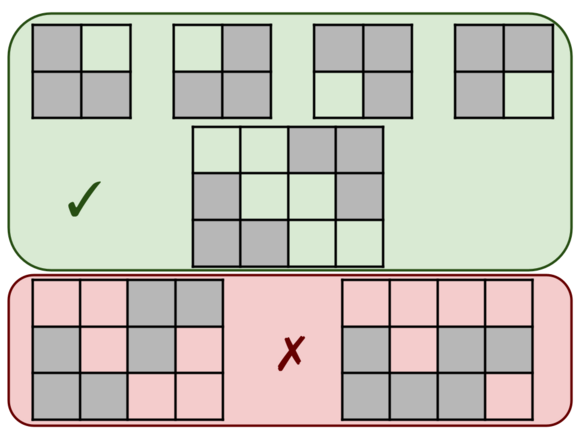
理论基础

• 回溯是一种纯暴力搜索的方法，它和递归相辅相成，通常是执行完递归之后紧接着执行回溯
• 相较于以往使用的for循环暴力搜索，回溯能解决更为复杂的问题，如以下的应用场景
• 应用场景
  • 组合问题
    • 如一个集合{1,2,3,4}，找出长度为2的组合
  • 排列问题
    • 相较于组合，排列是有顺序的，如{1,2}只有一种组合，但是有两种排列
  • 切割问题
    • 给一个字符串，给一个要求，求得怎么切割满足要求
  • 子集问题
    • 给一个集合，求它的子集
  • 棋盘问题
    • 如N皇后和解数独等
• 回溯法的思维结构——树型结构
  • 宽度代表集合的大小
  • 深度代表递归的深度
  • 

# 回溯编程模板
def backtracking(形参): # 返回值通常为空
    if (终止条件):
        存放结果
        return
        
    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）):
        处理节点
        backtracking(路径，选择列表) # 递归
        回溯，撤销处理结果

*77. 组合

题目链接/文章讲解：https://programmercarl.com/0077.%E7%BB%84%E5%90%88.html
视频讲解：https://www.bilibili.com/video/BV1ti4y1L7cv
剪枝操作：https://www.bilibili.com/video/BV1wi4y157er

• 考点
  • 回溯
• 我的思路
  • 思路不到位
• 视频讲解关键点总结
  • 回溯（递归）三要素
    • 形参：当前值，上限值，组合大小，单个组合变量，总组合结果变量；返回值为空
    • 退出条件：单个组合变量的大小等于组合大小，此时将单个组合变量加入总组合结果变量，并返回
    • 回溯逻辑
      • 不断地在范围内循环递归求取单个组合变量
      • 循环范围为当前值到上限值，每轮循环里：
        • 将当前值加入单个组合变量
        • 将当前值+1并递归
        • 执行回溯，即把单个组合变量里的最后一个值弹出，之后继续下一轮循环
    • 剪枝优化
      • 回溯题常常可以在循环范围上做优化
      • 本题可以把循环上限设置为上限值-（目标组合大小-当前组合大小）+2，+2是因为range函数在遍历时不包括右边界，所以要留出空余
• 我的思路的问题
  • 无思路
• 代码书写问题
  • 当想result变量添加单个组合变量时，要利用切片操作创建一个单个组合变量的副本并将该副本加入result，这是因为直接加入将仅仅把引用传入到result里，后续的改动将导致result里的同步改动
• 可执行代码

class Solution:
    def backtracking(self, cur, n, k, single_set, result):
        if len(single_set) == k:
            result.append(single_set[:])
            return
        for i in range(cur, n - (k - len(single_set)) + 2):
            single_set.append(i)
            self.backtracking(i + 1, n, k, single_set, result)
            single_set.pop()
    def combine(self, n: int, k: int) -> List[List[int]]:
        result = []
        self.backtracking(1, n, k, [], result)
        return result