P8680 [蓝桥杯 2019 省 B] 特别数的和
题目描述
小明对数位中含有 2、0、1、9 的数字很感兴趣(不包括前导 00),在 1 到 40 中这样的数包括 1、2、9、10 至 32、39 和 40,共28 个,他们的和是574。
请问,在 1 到 n 中,所有这样的数的和是多少?
输入格式
输入一行包含一个整数 �n。
输出格式
输出一行,包含一个整数,表示满足条件的数的和。
将输入的数按照不同的位数进行分类,然后将他们的每一项数位提取出来进行判断
如果符合条件则累加
#include<bits/stdc++.h>
using namespace std;
int a[6];
int main()
{
int sum=0;
int n;
cin>>n;
for(int i=1;i<=n;i++)
{
a[1]=i%10;//个位
a[2]=i/10%10;//十位
a[3]=i/100%10;//百位
a[4]=i/1000%10;//千位
a[5]=i/10000%10;//万位
if(i<10)
{
if(i==2||i==1||i==9)
{
sum+=i;
}
}
if(i>=10&&i<100)
{
for(int j=1;j<3;j++)
{
if(a[j]==2||a[j]==1||a[j]==9||a[j]==0)
{
sum+=i;
break;
}
}
}
if(i>=100&&i<1000)
{
for(int j=1;j<4;j++)
{
if(a[j]==2||a[j]==1||a[j]==9||a[j]==0)
{
sum+=i;
break;
}
}
}
if(i>=1000&&i<10000)
{
for(int j=1;j<5;j++)
{
if(a[j]==2||a[j]==1||a[j]==9||a[j]==0)
{
sum+=i;
break;
}
}
}
}
cout<<sum;
return 0;
}L-shapes
题目描述
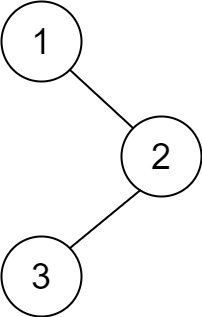
An L-shape is a figure on gridded paper that looks like the first four pictures below. An L-shape contains exactly three shaded cells (denoted by *), which can be rotated in any way.
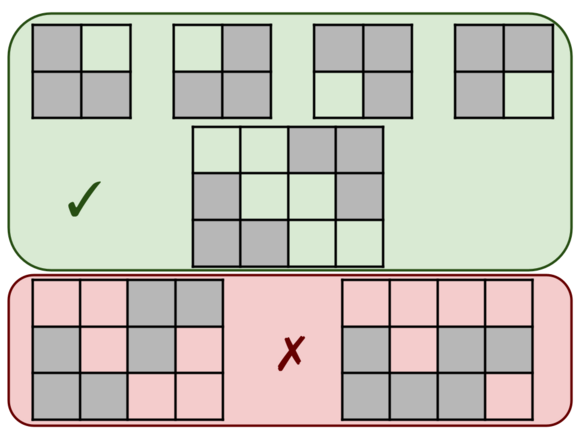
You are given a rectangular grid. Determine if it contains L-shapes only, where L-shapes can't touch an edge or corner. More formally:
- Each shaded cell in the grid is part of exactly one L-shape, and
- no two L-shapes are adjacent by edge or corner.
For example, the last two grids in the picture above do not satisfy the condition because the two L-shapes touch by corner and edge, respectively.
输入格式
The input consists of multiple test cases. The first line contains an integer t(1≤t≤100 ) — the number of test cases. The description of the test cases follows.
The first line of each test case contains two integers n and m ( 1≤n,m≤50 ) — the number of rows and columns in the grid, respectively.
Then n lines follow, each containing m characters. Each of these characters is either '.' or '*' — an empty cell or a shaded cell, respectively.
输出格式
For each test case, output "YES" if the grid is made up of L-shape that don't share edges or corners, and "NO" otherwise.
You can output the answer in any case (for example, the strings "yEs", "yes", "Yes" and "YES" will be recognized as a positive answer).
题意翻译
L形在网格纸上形如下面的前四张图片。L形正好包含三个阴影单元(用*表示),可以以任何方式旋转。
现给你一个矩形网格。确定它是否仅包含L形,其中L形不能接触边或角,也就是说网格中的每个阴影单元正好是一个L形的一部分,并且没有两个L形通过边或角相邻。
例如,上图中的最后两个网格不满足条件,因为两个L形分别通过角和边缘接触。
如果网格满足条件,则输出“YES”,否则输出“NO”。
遍历,当扫到*的时候,将其标记为1,遍历到1时对周围进行扫描,符合条件则将L型都变为0
最后再扫描时如果还扫到1则输出NO,否则输出YES
#include<bits/stdc++.h>
using namespace std;
int a[55][55],n,m,t;
char s;
void find(int i,int j)
{
if(a[i+1][j]&&a[i+1][j+1]&&!a[i-1][j-1]&&!a[i-1][j]&&!a[i-1][j+1]&&
!a[i][j-1]&&!a[i][j+1]&&!a[i][j+2]&&!a[i+1][j-1]&&!a[i+1][j+2]&&
!a[i+2][j-1]&&!a[i+2][j]&&!a[i+2][j+1]&&!a[i+2][j+2]){
a[i][j]=a[i+1][j]=a[i+1][j+1]=0;
return ;
}
if(a[i+1][j-1]&&a[i+1][j]&&!a[i-1][j-1]&&!a[i-1][j]&&!a[i-1][j+1]&&
!a[i][j-2]&&!a[i][j-1]&&!a[i][j+1]&&!a[i+1][j-2]&&!a[i+1][j+1]&&
!a[i+2][j-2]&&!a[i+2][j-1]&&!a[i+2][j]&&!a[i+2][j+1]){
a[i][j]=a[i+1][j-1]=a[i+1][j]=0;
return ;
}
if(a[i][j+1]&&a[i+1][j+1]&&!a[i-1][j-1]&&!a[i-1][j]&&!a[i-1][j+1]&&
!a[i-1][j+2]&&!a[i][j-1]&&!a[i][j+2]&&!a[i+1][j-1]&&!a[i+1][j]&&
!a[i+1][j+2]&&!a[i+2][j]&&!a[i+2][j+1]&&!a[i+2][j+2]){
a[i][j]=a[i][j+1]=a[i+1][j+1]=0;
return ;
}
if(a[i][j+1]&&a[i+1][j]&&!a[i-1][j-1]&&!a[i-1][j]&&!a[i-1][j+1]&&
!a[i-1][j+2]&&!a[i][j-1]&&!a[i][j+2]&&!a[i+1][j-1]&&!a[i+1][j+1]&&
!a[i+1][j+2]&&!a[i+2][j-1]&&!a[i+2][j]&&!a[i+2][j+1]){
a[i][j]=a[i][j+1]=a[i+1][j]=0;
return ;}
}
int main()
{
cin>>t;
for(int k=1;k<=t;k++)
{
memset(a,0,sizeof(a));
bool possible = true;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
cin>>s;
if(s=='*')
a[i][j]=1;
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(a[i][j]==1)
find(i,j);
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(a[i][j]==1)
{
possible=false;
break ;
}
}
if (!possible) break;
}
if (possible) {
cout << "YES\n";
} else {
cout << "NO\n";
}
}
return 0;
}P1258 小车问题
题目描述
甲、乙两人同时从 A 地出发要尽快同时赶到 B 地。出发时 A 地有一辆小车,可是这辆小车除了驾驶员外只能带一人。已知甲、乙两人的步行速度一样,且小于车的速度。问:怎样利用小车才能使两人尽快同时到达。
输入格式
仅一行,三个实数,分别表示 AB 两地的距离 s,人的步行速度 a,车的速度 b。
输出格式
两人同时到达 B 地需要的最短时间,保留 6 位小数。
列方程x/a=(s-2x+s-x)/b
解得时间=x/a+(s-x)/b
#include<bits/stdc++.h>
using namespace std;
int main()
{
double a,b,s,x;
cin>>s>>a>>b;
double t;
x=(2*a*s)/(3*a+b);
t=x/a+(s-x)/b;
cout<<fixed<<setprecision(6)<<t;
}P10050 [CCO2022] Alternating Heights
题目描述
Troy 计划给 CCO 的学生拍一张合影,他向你寻求帮助。
有 K 个学生,编号从 1 到 K。Troy 忘记了学生的身高,但他记得没有两个学生的身高相同。
Troy 有一个序列 1,2,…,A1,A2,…,AN,表示合影中从左到右的学生顺序。一个学生可能在 A 中出现多次。你不确定这张合影会怎么拍,但你不愿意认为 Troy 犯了错误。
Troy 会给你 Q 个形式为 x,y 的询问,每个询问为「给定学生序列 Ax,Ax+1,…,Ay,他们的身高能否形成一个交替序列?」更具体地说,我们用 hi 表示第 i 个学生的身高。如果存在一种身高分配h1,h2,…,hK,使得 hAx>hAx+1<hAx+2>hAx+3<…hAy,回答 YES;否则回答 NO。
注意,每个查询都是独立的:也就是说,询问 i 的身高分配与询问 j 的身高分配无关(i!=j)。
输入格式
第一行包含三个用空格分隔的整数 N,K 和 Q。
第二行包含 N 个整数,表示 1,2,…)A1,A2,…,AN(1≤Ai≤K)。
接下来的 Q 行,每行包含两个用空格分隔的整数 x 和 (1≤x<y≤N),表示一组查询。
输出格式
输出 Q 行。第 i 行,输出 YES 或者 NO,表示 Troy 的第 i 个查询的答案。
每次进行二分查找,将中间值和左端点进行拓扑排序
如果出现环则说明矛盾,输出NO
#include<bits/stdc++.h>
using namespace std;
int n,m,t,x,y,a[10005],f[10005];
int d[3005][3005],top[3005],in[3005];
queue<int> q;
bool check(int l,int r)
{
memset(in,0,sizeof(in));
memset(top,0,sizeof(top));
for(int i=l+1;i<=r;i+=2)
{
if(i-1>0) d[a[i]][++top[a[i]]]=a[i-1],in[a[i-1]]++;
if(i+1<=r) d[a[i]][++top[a[i]]]=a[i+1],in[a[i+1]]++;
}
while(!q.empty()) q.pop();
for(int i=1;i<=m;i++)
{
if(!in[i])
{
q.push(i);
}
}
int sum=0;
while(!q.empty())
{
int p=q.front();
q.pop();
sum++;
for(int i=1;i<=top[p];i++)
{
in[d[p][i]]--;
if(!in[d[p][i]])
q.push(d[p][i]);
}
}
return sum==m;
}
int F(int k)
{
int l=k,r=n,mid,p=0;
while(l<=r)
{
mid=(l+r)/2;
if(check(k,mid))
p=max(p,mid),l=mid+1;
else
r=mid-1;
}
return p;
}
int main()
{
cin>>n>>m>>t;
for(int i=1;i<=n;i++)
cin>>a[i];
for(int i=1;i<=n;i++)
f[i]=F(i);
for(int i=1;i<=t;i++)
{
cin>>x>>y;
if(y<=f[x])
{
cout<<"YES"<<endl;
}
else
{
cout<<"NO"<<endl;
}
}
return 0;
}