目录

最小生成树prim

最小生成树算法是一种用来在一个加权连通图中找到最小生成树的算法。最小生成树是一个包含图中所有顶点的树，其总权值最小。

prim算法

洛谷题目示例

P3366 【模板】最小生成树

题目描述

输入格式

输出格式

输入输出样例

说明/提示

题目分析

代码示例

---

最小生成树prim

最小生成树算法是一种用来在一个加权连通图中找到最小生成树的算法。最小生成树是一个包含图中所有顶点的树，其总权值最小。

常见的最小生成树算法包括：

1. Prim算法：从一个顶点开始，每次选择与当前生成树最近的顶点加入生成树中，直到所有顶点都被加入。Prim算法的时间复杂度为O(V^2)或O(ElogV)，其中V为顶点数，E为边数。

2. Kruskal算法：将所有边按权值从小到大排序，依次加入生成树中，但要保证加入的边不会形成环。Kruskal算法的时间复杂度为O(ElogE)或O(ElogV)，其中V为顶点数，E为边数。

这两种算法都可以用来求解最小生成树，选择哪种算法取决于具体情况和图的规模。（ 这里主要讲解第一种算法）

prim算法

Prim算法是一种用来在加权连通图中找到最小生成树的贪心算法。算法的基本思想是从一个初始顶点开始，逐步扩展生成树，每次选择与当前生成树最近的顶点加入生成树中，直到所有顶点都被加入。

具体步骤如下：

1. 选择一个初始顶点作为生成树的根节点，并将其加入生成树中。
2. 从生成树中的所有顶点出发，找到与生成树中的顶点相连且权值最小的边，将其连接的顶点加入生成树。
3. 重复上述步骤，直到所有顶点都被加入生成树为止。

Prim算法的时间复杂度取决于如何实现最小堆数据结构，通常为O(V^2)或O(ElogV)，其中V为顶点数，E为边数。Prim算法适用于稠密图或边的数量接近顶点数的情况。

总的来说，Prim算法是一种简单且有效的算法，用来求解加权连通图的最小生成树问题。 

洛谷题目示例

P3366 【模板】最小生成树

题目描述

如题，给出一个无向图，求出最小生成树，如果该图不连通，则输出 orz。

输入格式

第一行包含两个整数 N,M，表示该图共有 N 个结点和 M 条无向边。

接下来 M 行每行包含三个整数 Xi​,Yi​,Zi​，表示有一条长度为 Zi​ 的无向边连接结点 Xi​,Yi​。

输出格式

如果该图连通，则输出一个整数表示最小生成树的各边的长度之和。如果该图不连通则输出 orz。

输入输出样例

输入 #1复制

4 5
1 2 2
1 3 2
1 4 3
2 3 4
3 4 3

输出 #1复制

7

说明/提示

数据规模：

对于 20%的数据，N≤5，M≤20。

对于 40% 的数据，N≤50，M≤2500。

对于 70%的数据，N≤500，M≤104。

对于 100%100% 的数据：1≤N≤5000，1≤M≤2×105，1≤Zi​≤104。

样例解释：

 

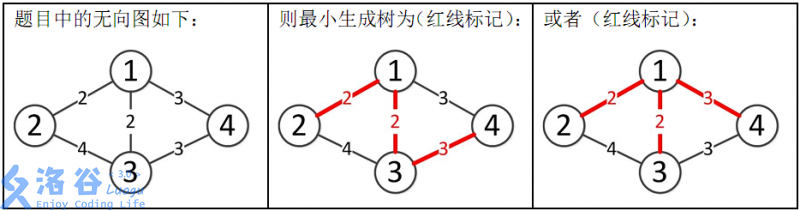
所以最小生成树的总边权为 2+2+3=7

题目分析

 1，模板题，不过注意测试数据存在平行边，如果用邻接矩阵存图的话应该存最短的平行边。

代码示例

#include<bits/stdc++.h>
using namespace std;
#define  Maxr 5001
int n,m;
int mp[Maxr][Maxr];
bool vis[Maxr];
int dist[Maxr];
int Prim()
{
    int sum=0;
    memset(dist,0x7f,sizeof(dist));
    vis[1]=true;
    for(int i=1; i<=n; i++)dist[i]=mp[1][i];//首先把第一个顶点录入，所以下一个循环是i<n
    for(int i=1; i<n; i++)//由于第一个顶点已经录入权值，所以循环n-1次
    {
        int minn=0x7f7f7f7f,minj=0;
        for(int j=1; j<=n; j++)
        {
            if(!vis[j]&&dist[j]<minn)//未走过的节点中权最小的节点的位置
            {
                minn=dist[j];
                minj=j;
            }
        }
        if(!minj)return -1;
        sum+=minn;//累加提前，避免闭环
        vis[minj]=true;
        for(int j=1; j<=n; j++)
        {     //依次更新后面没走过的点的权最小值
            if(!vis[j])dist[j]=min(dist[j],mp[minj][j]);
        }

    }

return sum;
}
int main()
{
    memset(mp,0x7f,sizeof(mp));
    cin>>n>>m;
    for(int i=0; i<m; i++)
    {
        int x,y,z;
        cin>>x>>y>>z;
        mp[x][y]=mp[y][x]=min(mp[x][y],z);//邻接矩阵存图
    }

    int sum=Prim();
    if(sum==-1)cout<<"orz"<<endl;
    else cout<<sum<<endl;
    return 0;





}

如果以上有啥问题，还望大佬能指正下哈