题目

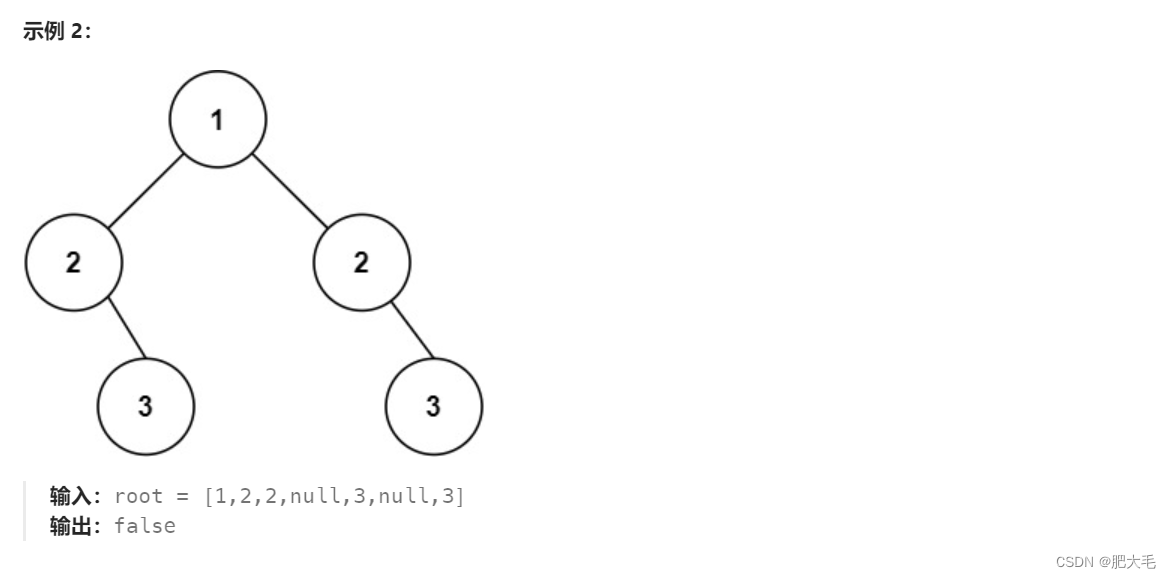
106. 从中序与后序遍历序列构造二叉树

分析

前面讲过根据前序和中序构建二叉树：博客链接
这道题是告诉我们一颗二叉树的后序和中序，让我们根据后序和中序构造出整颗二叉树。
拿到这道题，我们首先要知道中序的后序又怎样的性质：

• 中序：【左 根 右】
• 后序：【左 右 根】

根据以上的性质，我们可以得到以下的结论：

• 后序遍历的最后一个元素一定为数的根节点node的值。
• 因为题目告诉了我们无重复元素，所以在中序遍历中找到根节点 node 的索引，可以将 中序遍历的数组 划分为 【左子树 | 根节点 | 右子树】 的形式。
• 在中序遍历数组中我们可以知道以 node 为根节点，左右子树的节点个数，利用这点可以将 后序遍历数组 划分为 【左子树 | 右子树 根节点 】。
• 通过上面我们可以知道整颗树的树根，左子树，右子树。下面需要分别构建左子树、右子树，还是按照上面的逻辑。

接下来的问题就是需要知道构建左子树和右子树的时候的前序序列和中序序列。

• 根节点的值为 postorder[postorder.length-1]，然后在中序序列中找到这个节点下标为 rootInorderIndex
• 构建左子树：

左子树的 inorder :[0,rootInorderIndex)
左子树的 postorder :[0,rootInorderIndex)

• 构建右子树：

右子树的 inorder :[rootInorderIndex+1,inorder.length)
右子树的 postorder :[rootInorderIndex,postorder.length - 1)

代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        if(inorder.length == 0) return null;
        int rootValue = postorder[postorder.length - 1];
        TreeNode root = new TreeNode(rootValue);
        int rootInorderIndex = -1;
        for(int i = 0;i < inorder.length;i ++) {
            if(inorder[i] == rootValue) {
                rootInorderIndex = i;
                break;
            }
        }
        root.left = buildTree(Arrays.copyOfRange(inorder,0,rootInorderIndex),Arrays.copyOfRange(postorder,0,rootInorderIndex));
        root.right = buildTree(Arrays.copyOfRange(inorder,rootInorderIndex+1,inorder.length),Arrays.copyOfRange(postorder,rootInorderIndex,postorder.length - 1));
        return root;
    }
}