今日题目:
- 704. 二分查找
- 35. 搜索插入位置
- 34. 在排序数组中查找元素的第一个和最后一个位置
目录
- 今日总结
- Problem 1: 二分法
- LeetCode 704. 二分查找 【easy】
- LeetCode 35. 搜索插入位置 ⭐⭐⭐⭐⭐
- LeetCode 34. 在排序数组中查找元素的第一个和最后一个位置 【medium】
今日总结
重点学习了使用二分法来解决问题,需要特别理解的是,二分法在通过 while(low <= high) 循环后,low 与 high 的关系所呈现出来的性质,以及为什么能够呈现这样的性质。利用这个性质可以更容易地解决相关问题。
Problem 1: 二分法
LeetCode 704. 二分查找 【easy】
704. 二分查找 | LeetCode
这个题目很经典,题目本身很简单,但这里有一种具有普适性的写法,可以用来解决其他二分查找相关的题目,这里需要着重学习一下:

关键理解好二分法在经过 while(low <= high) 这个循环后,low 和 high 所呈现出来的结果的性质:
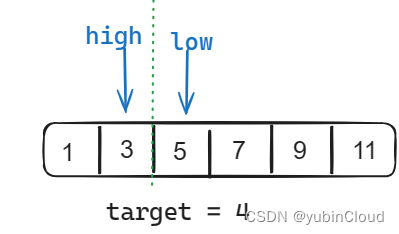
- high 最后一定是在 low 左边,而且 high == low - 1,形成一个交错
- low 和 high 中间将数字序列划分成了两个部分:
- 左半边从开始到 high 为止,都是小于 target
- 右半边从 low 到结束,都是大于等于 target
为什么会具备这样的性质?
简单来说,因为 while 的判断是low <= high,所以最终 low 一定是大于 high。
同时,low 和 high 每次更新都是基于 mid 来向前或向后一步走,而 mid 是一定出现在 [low,high] 这个区间内,所以每次更新的结果是,low 或 high 一定是处于原先 [low,high] 范围内或者这个范围的左边或右边一个为止。所以,最终一定是high == low - 1。
当然,目前也很容易理解 [0, high] 一定是小于 target,[low, end) 一定是大于等于 target。因为当nums[mid] == target时,我们是将 high 移动到 mid 左边,这样的结果就是让等于 target 元素的值出现在了 high 右边,所有右半边才会有等于 target 的元素。
在上面的代码中,low 最终指向的是第一个大于等于 target 的元素,但由于 target 可能不存在,所以在作为结果返回时,需要判断一下 low 是否在 nums 的合法范围内,以及 low 指向的值是否等于 target。
学会了这个题目,下面几个题目就是可以利用这里总结的性质来解决。
LeetCode 35. 搜索插入位置 ⭐⭐⭐⭐⭐
35. 搜索插入位置 | LeetCode
通过这个题,对二分法的思路有了更深入的理解。
这个题目是返回搜索的位置或者插入的位置,自然也就是 low 的位置,所以代码如下:

整体与第一个二分法的题目一样,只是最后直接把 low 给 return 出去而已。
所以,学习二分法需要注意:
- 代码中 while 的条件、low 与 high 变更的方式
- 经过 while 循环后 low 与 high 所呈现出来的性质
LeetCode 34. 在排序数组中查找元素的第一个和最后一个位置 【medium】
34. 在排序数组中查找元素的第一个和最后一个位置 | LeetCode
这个题目就有难度了,解决这个题目,需要依靠我们在上面的题目中总结出来的经验。
由于题目要求复杂度 O ( log n ) O(\log n) O(logn),所以需要通过两次二分查找来分别找到左边界和右边界。
刚刚我们总结到,当经过 while 循环后,low 指向了第一个大于等于 target 的元素,这不就是这个题目的左边界嘛!所以,我们可以写出找左边界的代码,但是因为这个题目中 nums 中的数字是可能重复的,所以我们需要做一些更改:
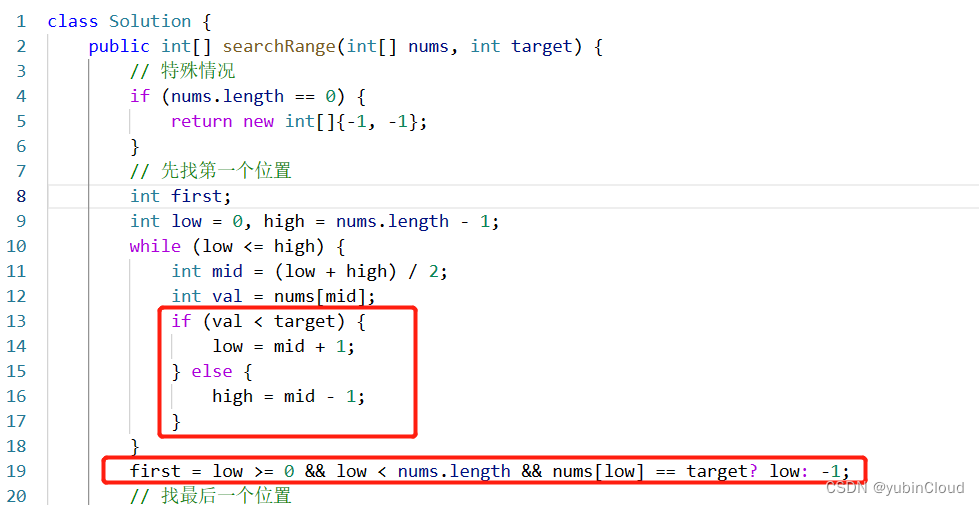
这个代码有两点需要我们特别关注:
- 当
val == target的时候,我们是更新 low 还是 high? - 左边界和 low 的关系?
在上面代码中,如果 val == target,那么就让 high 移动到 mid 左边,这样的结果就是当 while 循环完之后,等于 target 的元素都出现在了右半边,也就是 [low, end) 这个区间内,所以 low 才成了左边界。
同时因为 low 可能超出 nums 的索引范围,以及可能没有找到 target,所以给左边界 first 赋值时需要检查一下,检查不通过就是赋值 -1,代表没有找到。
根据刚刚的思路,当 val == target 时,如果我们让 low 移动到 mid 右边,那么 while 循环完的结果就变成了 “target 的元素都出现了左半边”,也就是 [0, high] 这个区间,所以 high 自然就成了右边界。
所以寻找右边界的二分写法是:
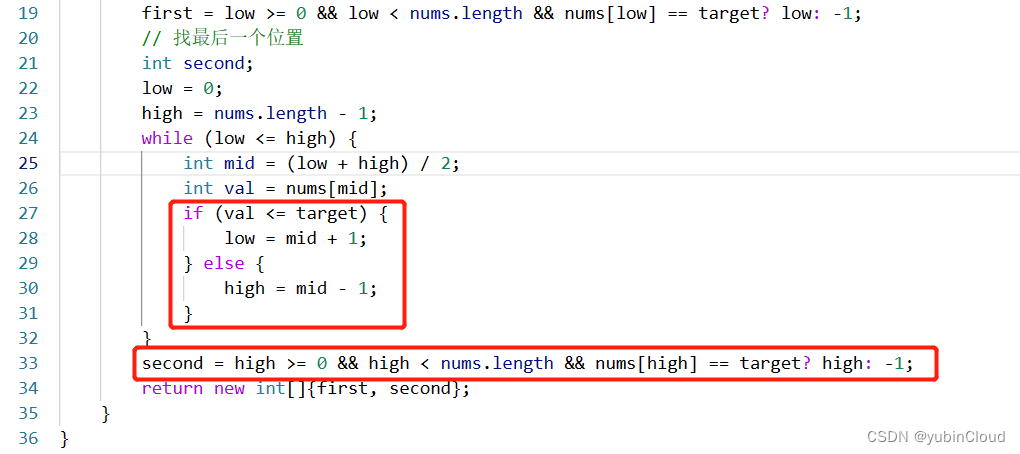
注意这里与找左边界的区别。