压缩感知是一种用于高效获取和表示信号的技术，它可以显著减少数据的采样和传输量，同时保持对信号的高质量恢复能力。在压缩感知中，信号被表示为其在一个稀疏基中的稀疏线性组合。通过仅使用少量的随机投影测量，就能够捕捉信号的大部分信息，并且可以利用优化方法恢复原始信号。

MATLAB是一种功能强大的数值计算和科学编程工具，它提供了丰富的工具箱和函数来支持压缩感知的仿真和实现。其中一个常用的工具是l1_image软件包，它提供了一种基于l1范数最小化的方法，用于压缩感知图像恢复。

通过调用l1_image，我们可以在MATLAB环境中轻松地对压缩感知方法进行仿真和实验。l1_image提供了一系列函数来生成随机投影矩阵、计算稀疏表示、执行l1范数最小化等操作。通过使用这些函数，我们可以通过少量的测量数据恢复出高质量的原始图像。

在本文中，我们将详细介绍如何使用MATLAB中的l1_image工具包来实现压缩感知图像恢复。

仿真实现

下面我们看看MATLAB如何实现

MATLAB代码

计算量太大了，仅仅选取了lena眼睛的部分，大概在([250:299],[250:299])区域内选择一块roi就好了。
具体代码如下：
【说明】本代码来源于MATLAB网站，网址在最后。

% compressed sensing example
%
%___DESCRIPTION___
% MATLAB implementation of compressive sensing example as described in R.
% Baraniuk, Compressive Sensing, IEEE Signal Processing Magazine, [118],
% July 2007. The code acquires 250 averaged random measurements of a 2500
% pixel image. We assume that the image has a sparse representation in the
% DCT domain (not very sparse in practice). Hence the image can be
% recovered from its compressed form using basis pursuit.
%
%___DEPENDENCIES___
% Requires the MATLAB toolbox l_1-MAGIC: Recovery of Sparse Signals via Convex
% Programming v1.11 by J. Candes and J. Romberg, Caltech, 2005. 
%
%___VARIABLES___
% x = original signal (nx1) y = compressed signal (mx1) Phi = measurement
% matrix (mxn) Psi = Basis functions (nxn) Theta = Phi * Psi (mxn) s =
% sparse coefficient vector (to be determined) (nx1)
%
%___PROBLEM___
% Invert the matrix equation y = Theta * s and therefore recover hat_x as
% k-sparse linear combination of basis functions contained in Psi. Note
% also that y = Phi * x.
%
%___SOLUTION___
% Let Phi be a matrix of i.i.d. Gaussian variables. Solve matrix inversion
% problem using basis pursuit (BP).

%___CREATED___
% o By S.Gibson, School of Physical Sciences, University of Kent. 
% o 1st May, 2013.
% o version 1.0
% o NOTES: If the max number of iterations exceeds 25, error sometimes
%   occurs in l1eq_pd function call.
%
%___DISCLAIMER___
% The code below is my interpretation of Baraniuk's compressed sensing
% article. I don't claim to be an authority on the subject!


%___INPUT IMAGE___
clear, close all, clc
A = imread('lenaGray.bmp');
% A = A([50:99],[50:99]);
A = A([250:299],[250:299]); % 提取图像的一个子区域
x = double(A(:));
n = length(x);

%___MEASUREMENT MATRIX___
m = 1000; % NOTE: small error still present after increasing m to 1500;
Phi = randn(m,n);
    %__ALTERNATIVES TO THE ABOVE MEASUREMENT MATRIX___ 
    %Phi = (sign(randn(m,n))+ones(m,n))/2; % micro mirror array (mma) e.g. single
    %pixel camera Phi = orth(Phi')'; % NOTE: See Candes & Romberg, l1
    %magic, Caltech, 2005.

%___COMPRESSION___
y = Phi*x;

%___THETA___
% NOTE: Avoid calculating Psi (nxn) directly to avoid memory issues.
Theta = zeros(m,n);
for ii = 1:n
    ii
    ek = zeros(1,n);
    ek(ii) = 1;
    psi = idct(ek)';
    Theta(:,ii) = Phi*psi;
end

%___l2 NORM SOLUTION___ s2 = Theta\y; %s2 = pinv(Theta)*y
s2 = pinv(Theta)*y;

%___BP SOLUTION___
s1 = l1eq_pd(s2,Theta,Theta',y,5e-3,20); % L1-magic toolbox
%x = l1eq_pd(y,A,A',b,5e-3,32);

%___DISPLAY SOLUTIONS___
plot(s2,'b'), hold
plot(s1,'r.-')
legend('least squares','basis pursuit')
title('solution to y = \Theta s')

%___IMAGE RECONSTRUCTIONS___
x2 = zeros(n,1);
for ii = 1:n
    ii
    ek = zeros(1,n);
    ek(ii) = 1;
    psi = idct(ek)';
    x2 = x2+psi*s2(ii);
end

x1 = zeros(n,1);
for ii = 1:n
    ii
    ek = zeros(1,n);
    ek(ii) = 1;
    psi = idct(ek)';
    x1 = x1+psi*s1(ii);
end

figure('name','Compressive sensing image reconstructions')
subplot(1,3,1), imagesc(reshape(x,50,50)), xlabel('original'), axis image
subplot(1,3,2), imagesc(reshape(x2,50,50)), xlabel('least squares'), axis image
subplot(1,3,3), imagesc(reshape(x1,50,50)), xlabel('basis pursuit'), axis image
colormap gray

测试结果

看下第2种的整体效果还可以，这里对源程序的观察值略做了修改。
源程序选的的250个观察值，相当于250/2500，十分之一。
这里选取了1000个，1000/2500，大概四分之一。
十分之一的效果大家可以测试一下，效果非常不好。
第一种很拉胯。

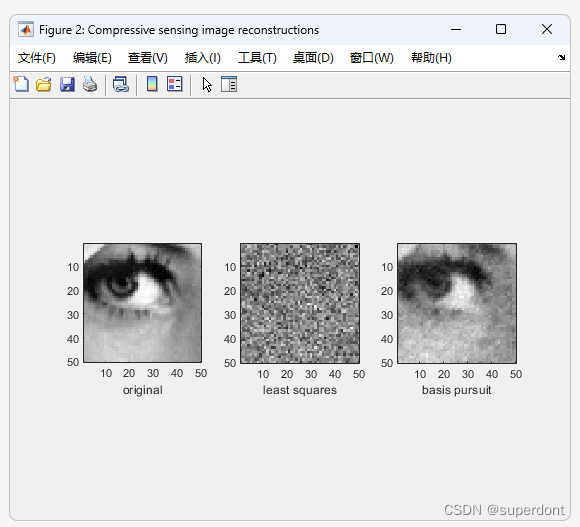
增加到2000个点的效果：
可以看到明显好了很多。

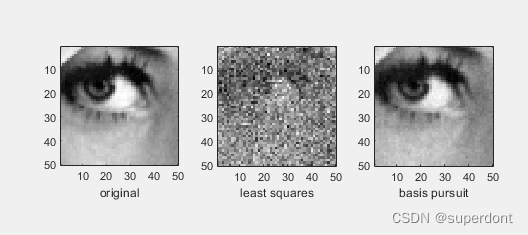
增加到2200个点的效果：

哈哈哈哈哈哈哈，2500个点，

部分注释

矩阵逆运算

s2 = pinv(Theta)*y 是一种使用广义逆运算（generalized inverse operation）求解线性方程组的方法，其中 pinv(Theta) 表示矩阵 Theta 的Moore-Penrose伪逆（pseudo-inverse）。这个方法是使用最小二乘法（least squares method）来估计线性方程组的解。

在给定线性方程组 y = Theta * s 的情况下，其中 y 是已知的观测向量，Theta 是系统的矩阵，s 是未知的向量，我们希望寻找一个解 s2，使得 Theta * s2 尽可能接近观测向量 y。然而，在实际问题中，往往无法直接求解 s。这时，我们可以使用最小二乘法来近似求解。

求解的步骤如下：

1. 计算矩阵 Theta 的 Moore-Penrose 伪逆 pinv(Theta)，它是一个满足 Theta * pinv(Theta) * Theta = Theta 和 pinv(Theta) * Theta * pinv(Theta) = pinv(Theta) 的矩阵。
2. 将 y 与 pinv(Theta) 相乘，得到近似的解 s2。

这样，s2 就是通过最小二乘法来估计线性方程组的解。它是一种经典的求解方法，在信号处理和线性代数中经常使用。然而，需要注意的是，在特定的问题情况下，使用其他方法可能会提供更好的结果，特别是在信号是稀疏的情况下。

求解稀疏矩阵

s1 = l1eq_pd(s2,Theta,Theta',y,5e-3,20);
这行代码是使用 L1-magic工具箱（一个专门用于解决稀疏重构问题的 MATLAB 工具箱）来求解压缩感知（Compressed Sensing）问题的一部分。在上述代码中，具体使用的是基于原始-对偶内点法（Primal-Dual Interior-Point Method）的L1范数最小化算法，目的是求解等式约束下的L1最小化问题。

这里是函数 l1eq_pd 的基本使用语法及含义：

• s1：是求解的稀疏信号估计值，即原始信号在稀疏域中的表示。
• l1eq_pd：是L1-magic工具箱中用于解决等式约束L1最小化问题的函数名。
• s2：是最小化过程的初始解，通常可以是一个零向量，但这里用的是前面得到的最小二乘解（可能是为了提供一个更好的起点，加速算法的收敛）。
• Theta：是测量矩阵或传感矩阵与稀疏基的乘积矩阵。
• Theta'：是Theta矩阵的转置。
• y：是已知的观测向量，也就是压缩感知中的测量结果。
• 5e-3：是一个正则化参数，这个参数可以平衡稀疏约束和数据保真度之间的权重，经常需要通过实验来选择一个合适的值。
• 20：可能是算法迭代的次数，或者是内点法中某个容忍度的设置。

这个函数将最小化以下的目标函数：

minimize ||s||_1 subject to Theta * s = y

这里的 ||s||_1 表示的是向量 s 的 L1 范数，即其所有元素绝对值的和。这种L1最小化在 s 预计是稀疏的情况下尤其有用，因为它倾向于产生只有少数非零项的解，这与压缩感知理论中的稀疏性假设相吻合。

总结来说，这个命令是尝试在给定等式约束下通过L1最小化来寻找一个解 s1，该解中非零项的数量尽可能少，同时解应尽可能地符合原始问题的约束 Theta * s = y。

参考资料：

1、主体程序网址：
simple compressed sensing example
2、l1_image网址：
l1_image

相关博文

理解并实现OpenCV中的图像平滑技术

OpenCV中的边缘检测技术及实现

OpenCV识别人脸案例实战

入门OpenCV：图像阈值处理

我的图书

下面两本书欢迎大家参考学习。

OpenCV轻松入门

李立宗，OpenCV轻松入门，电子工业出版社，2023
本书基于面向 Python 的 OpenCV(OpenCV for Python)，介绍了图像处理的方方面面。本书以 OpenCV 官方文档的知识脉络为主线，并对细节进行补充和说明。书中不仅介绍了 OpenCV 函数的使用方法，还介绍了函数实现的算法原理。

在介绍 OpenCV 函数的使用方法时，提供了大量的程序示例，并以循序渐进的方式展开。首先，直观地展示函数在易于观察的小数组上的使用方法、处理过程、运行结果，方便读者更深入地理解函数的原理、使用方法、运行机制、处理结果。在此基础上，进一步介绍如何更好地使用函数处理图像。在介绍具体的算法原理时，本书尽量使用通俗易懂的语言和贴近生活的实例来说明问题，避免使用过多复杂抽象的公式。

本书适合计算机视觉领域的初学者阅读，包括在校学生、教师、专业技术人员、图像处理爱好者。
本书第1版出版后，深受广大读者朋友的喜爱，被很多高校选为教材，目前已经累计重印9次。为了更好地方便大家学习，对本书进行了修订。

计算机视觉40例

李立宗，计算机视觉40例，电子工业出版社，2022
近年来，我深耕计算机视觉领域的课程研发工作，在该领域尤其是OpenCV-Python方面积累了一点儿经验。因此，我经常会收到该领域相关知识点的咨询，内容涵盖图像处理的基础知识、OpenCV工具的使用、深度学习的具体应用等多个方面。为了更好地把所积累的知识以图文的形式分享给大家，我将该领域内的知识点进行了系统的整理，编写了本书。希望本书的内容能够对大家在计算机视觉方向的学习有所帮助。
本书以OpenCV-Python（the Python API for OpenCV）为工具，以案例为载体，系统介绍了计算机视觉从入门到深度学习的相关知识点。
本书从计算机视觉基础、经典案例、机器学习、深度学习、人脸识别应用等五个方面对计算机视觉的相关知识点做了全面、系统、深入的介绍。书中共介绍了40余个经典的计算机视觉案例，其中既有字符识别、信息加密、指纹识别、车牌识别、次品检测等计算机视觉的经典案例，也包含图像分类、目标检测、语义分割、实例分割、风格迁移、姿势识别等基于深度学习的计算机视觉案例，还包括表情识别、驾驶员疲劳监测、易容术、识别年龄和性别等针对人脸的应用案例。
在介绍具体的算法原理时，本书尽量使用通俗易懂的语言和贴近生活的示例来说明问题，避免使用复杂抽象的公式来介绍。
本书适合计算机视觉领域的初学者阅读，适于在校学生、教师、专业技术人员、图像处理爱好者使用。