---

每次从最小质数开始遍历，可以保证n只会被最小质数筛到， 避免多次筛到， 每个数只会被筛一次， 即时间复杂度为$O(n)$， 线性筛法

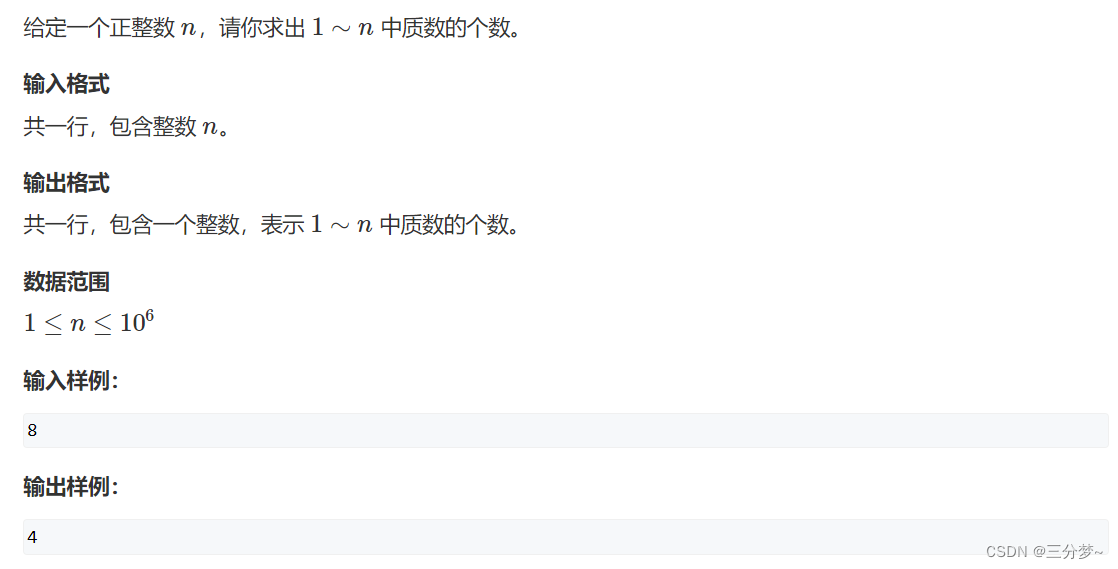
筛法求质数

原题链接：筛质数

每次从最小质数开始遍历，可以保证n只会被最小质数筛到， 避免多次筛到， 每个数只会被筛一次， 即时间复杂度为$O(n)$， 线性筛法

#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int primes[N];
bool st[N];
int n;
int get_primes(int n) {
    if(n < 2)   return 0;
    int cnt = 0;
    for(int i = 2; i <= n; i++ ) {	//一次线性筛选，即可完成操作
        if(!st[i]) primes[cnt++] = i;	//没被筛到，则为质数
        for(int j = 0; primes[j] * i <= n; j++) {
            st[primes[j] * i] = true;	//从最小质数集开始筛选相关合数
            if(i % primes[j] == 0)  break;	//找到最小质因数，直接操作结束
        }
    }
    return cnt;
}
int main() {
    cin >> n;
    cout << get_primes(n);
    return 0;
}

欧拉函数

基本模板

原题链接：欧拉函数

---

#include <iostream>
#include <unordered_map>
using namespace std;
int euler(int x) {
    int res = x;
    for(int i = 2; i <= x / i; i++) {
        if(x % i == 0) {
            res = res / i * (i - 1);
            while(x % i == 0)    x /= i;
        }
    }
    if(x > 1)   res = res / x * (x - 1);
    return res;
}

int main() {
    int n;
    cin >> n;
    while(n --) {
        int a;
        cin >> a;
        cout << euler(a) << endl;
    }
    return 0;
}

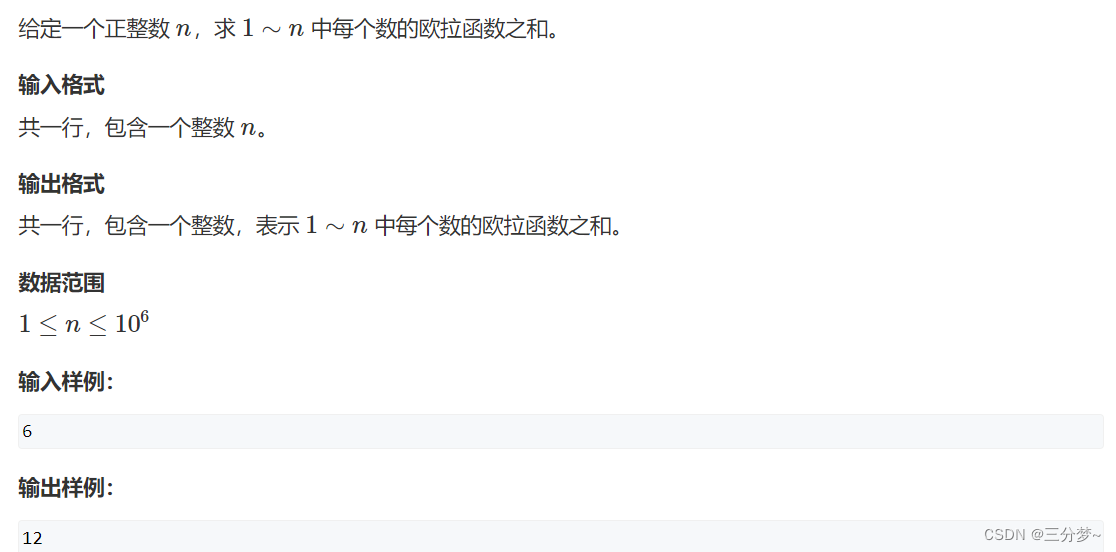
筛法求欧拉函数

原题链接

欧拉推导式可根据容斥原理推出

代码如下：

//欧拉：1 ~ n - 1 中与n互质的数的个数
#include <iostream>
#include <bitset>
using namespace std;
const int N = 1e6 + 10;
int primes[N], cnt;
int phi[N];
bitset<N> st;
long long get_eulers(int n) {
    long long res = 0;
    phi[1] = 1;
    for(int i = 2; i <= n; i++) {   //线性筛法，遍历一次n
        if(!st[i]) {    //没有被筛，质数
            primes[cnt++] = i;
            phi[i] = i - 1; //若为质数，则代表1 ~ i - 1都为互质
        }
        for(int j = 0; primes[j] <= n / i; j++) {
            st[primes[j] * i] = 1;
            if(i % primes[j] == 0)  {
                //若primes[j]为i的质因数，则有 primes[j] 的质因子必然存在于i中
                phi[i * primes[j]] = primes[j] * phi[i];
                break;
            }
            //若i % primes[j] != 0，则对质数primes[j]另行计算有:p[j] * (p[j] - 1) / p[j]
            phi[i * primes[j]] = phi[i] * (primes[j] - 1);
        }
    }
    for(int i = 1; i <= n; i++) res += phi[i];
    return res;
}
int main() {
    int n;
    cin >> n;
    cout << get_eulers(n); 
    return 0;
}