最优二叉搜索树 C#实现

news2024/10/6 5:59:09

最优二叉搜索树 C#实现

介绍一下

上一篇博文搞半天挺烧脑，没搞清楚继续… 主要是练习动态规划算法。最关键的一个是这个最优二叉搜索树能干啥。我认为如果数据稳定，统计出概率来，用最优二叉树保存，以后搜索应该是效率比较高的。还有一个是通过一通研究这个算法，折磨半天自己，加深理解，动态规划是真的难。
dp表项一个是概率之和的理解，一个是dp状态转义表的理解。

概率之和递推公式

if (j < i)//看条件判定没有任何数值的树概率就是间隙的概率
dp[i, j].weight = probs[2 * j];
else//递推数值之前的概率 + 数值概率 + 数值和之后的间隙概率
dp[i, j].weight = dp[i, j - 1].weight + probs[2 * j - 1] + probs[2 * j];

状态转移递推公式

//赋值一个比较大的数字，可以知道，搜索长度最大不会超过数组长度
dp[h, l].path = datas.Count;
for (int k = h; k <= l; k++)
{
//通过getpath函数兼容索引后面小于前面的情况，节省空间。
float path = GetPath(h, k - 1, dp) + GetPath(k + 1, l, dp) + dp[h, l].weight;
if (dp[h, l].path > path)
{
//冒泡比较记录最小搜索路长和树的根，以便于创建树
dp[h, l].path = path;
dp[h, l].root = k;
}
}

根据转移表递归创建搜索树

主要是CreateBSTNode函数
开始大于结束直接返回空，没有树结点
开始等于结束返回单一结点
开始小于结束，进入递归

程序数据和结果

List<int> lst = new List<int> { 10, 20, 30, 40, 50, 60 };
//间隙 数值 间隙 数值 ... 间隙
List<float> fls = new List<float> { 0.05f, 0.05f, 0.1f, 0.1f, 0.05f, 0.05f, 0.05f, 0.1f, 0.05f, 0.2f, 0.1f,0.01f,0.09f };
//创建最优二叉搜索树，准备绘制
bTree = BSTree.CreateOPSTree(lst, fls);

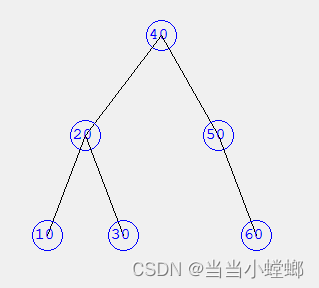
在这里插入图片描述

程序核心代码

dp表项

    public struct Item
    {
        //概率之和[权重]
        public float weight;
        //最短平均路长[状态转移表]
        public float path;
        //根节点
        public int root;
    }

构建搜索树代码

private static float GetPath(int h, int l, Item[,] items)
{
    if (h > l)
    {
        return 0.0f;
    }
    else
    {
        return items[h, l].path;
    }
}

/// <summary>
/// 根据dp转移表构建树
/// </summary>
/// <param name="h">开始</param>
/// <param name="l">结束</param>
/// <param name="dps">转移表</param>
/// <param name="datas">树结点数据</param>
/// <returns></returns>
private static BSTree CreateBSTNode(int h, int l, Item[,] dps, List<int> datas)
{
	//开始大于结束
    if (h > l)
    {
        return null;
    }

//开始等于结束
    if (h == l)
    {
        return new BSTree(datas[dps[h,l].root - 1]);
    }
    else//开始小于结束 进入递归
    {
        BSTree bSTree = new BSTree(datas[dps[h, l].root - 1]);
        bSTree.lChild = CreateBSTNode(h, dps[h,l].root-1,dps, datas);
        bSTree.rChild = CreateBSTNode(dps[h, l].root + 1, l, dps, datas);
        return bSTree;
    }
}

public static BSTree CreateOPSTree(List<int> datas, List<float> probs)
{
    Item[,] dp = new Item[datas.Count + 1, datas.Count + 1];
    //赋值概率
    for (int i = 1; i <= datas.Count; i++)
    {
        for (int j = i - 1; j <= datas.Count; j++)
        {
            if (j < i)
                dp[i, j].weight = probs[2 * j];
            else
                dp[i, j].weight = dp[i, j - 1].weight + probs[2 * j - 1] + probs[2 * j];
        }
    }

    //赋值dp转移表
    for (int len = 1; len <= datas.Count; len++)
    {
        for (int h = 1, l= len; h <= datas.Count && l<= datas.Count; h++, l++)
        {
            dp[h, l].path = datas.Count;
            for (int k = h; k <= l; k++)
            {
                float path = GetPath(h, k - 1, dp) + GetPath(k + 1, l, dp) + dp[h, l].weight;
                if (dp[h, l].path > path)
                {
                    dp[h, l].path = path;
                    dp[h, l].root = k;
                }
            }
        }
    }

    return CreateBSTNode(1, datas.Count, dp,datas);
}