📝个人主页：五敷有你      

 🔥系列专栏：算法分析与设计

⛺️稳中求进，晒太阳

题目

给你一个二叉树的根节点 root。设根节点位于二叉树的第 1 层，而根节点的子节点位于第 2 层，依此类推。

请返回层内元素之和 最大 的那几层（可能只有一层）的层号，并返回其中 最小 的那个。

示例

示例 1：

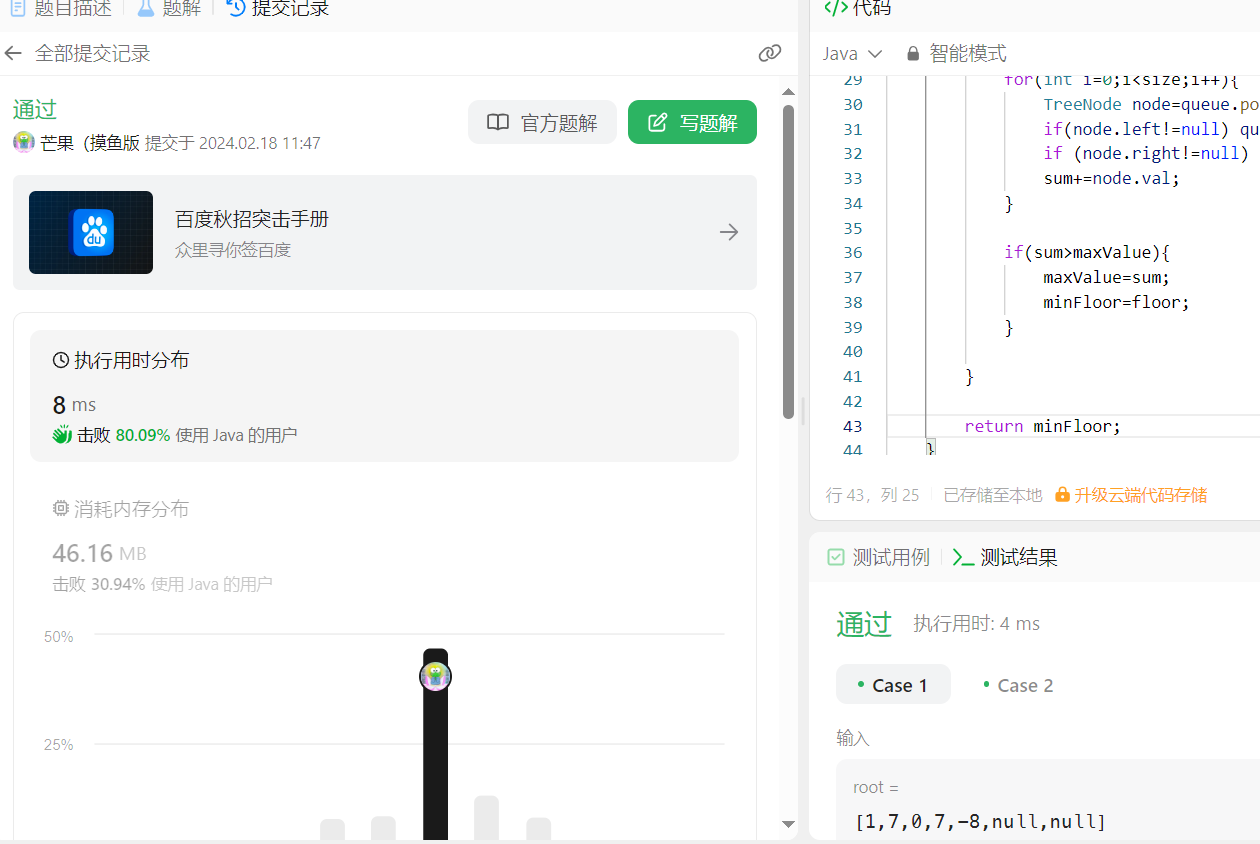
输入：root = [1,7,0,7,-8,null,null]
输出：2
解释：
第 1 层各元素之和为 1，
第 2 层各元素之和为 7 + 0 = 7，
第 3 层各元素之和为 7 + -8 = -1，
所以我们返回第 2 层的层号，它的层内元素之和最大。

示例 2：

输入：root = [989,null,10250,98693,-89388,null,null,null,-32127]
输出：2

思路（树的层次遍历的简单变形）

树的层次遍历是一种按照树的层级顺序逐层遍历节点的方法。在层次遍历中，首先访问树的根节点，然后依次访问每一层的节点，从上到下、从左到右地顺序访问。这种遍历方式通常使用广度优先搜索（BFS）算法实现。

具体步骤如下：

1. 从树的根节点开始，将根节点放入队列中。
2. 从队列中取出一个节点，访问该节点。
3. 将该节点的所有子节点（如果有）依次放入队列中。
4. 重复步骤 2 和步骤 3，直到队列为空。

层次遍历的特点是，它保证了在遍历过程中，同一层的节点会先于下一层的节点被访问。这种遍历方式对于需要按层级处理树节点的情况非常有用，例如在解决本问题中，需要计算每一层节点的元素之和，因此使用层次遍历能够很方便地实现这个目标。

代码实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int maxLevelSum(TreeNode root) {
        Queue<TreeNode> queue=new LinkedList();
        queue.offer(root);
        int maxValue=Integer.MIN_VALUE;
        int minEle=Integer.MAX_VALUE;
        int minFloor=0;
        int floor=0;
        while (!queue.isEmpty()){
            int size=queue.size();
            int sum=0;
            floor++;
        
            for(int i=0;i<size;i++){
                TreeNode node=queue.poll();
                if(node.left!=null) queue.offer(node.left);
                if (node.right!=null) queue.offer(node.right);
                sum+=node.val;
            }
          
            if(sum>maxValue){
                maxValue=sum;
                minFloor=floor;
            }

        }
     
        return minFloor;
    }
}

运行结果