LeetCode算法实践——前缀和从入门到入土

news2025/1/12 21:06:25

前缀和算法

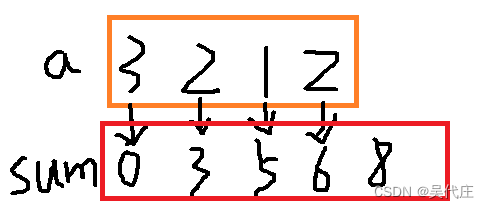
对于一个数组a，和为s数组；其每一个下标的前缀和为s[0]=0,s[i]=s[i-1]+a[i]。

从上面可以推导出left到right之间的前缀和为是s[right+1]-s[left]。

例如a=[3,2,1,2]，对应的前缀和数组为s=[0,3,5,6,8]。a的子数组[2,1,2]的和就可以用s[4]−s[1]=8−3=5算出来。
在这里插入图片描述

算法实践

LeetCode 930. 和相同的二元子数组

给你一个二元数组nums，和一个整数goal，请你统计并返回有多少个和为goal的非空子数组。

解题思路

定义前缀和数组sum，如果i…j之间和为goal，那么有sum[j]-sum[i]=goal。因此可以枚举j即可。实际解题时可以用哈希记录每一种前缀和出现的次数。

class Solution {
    public int numSubarraysWithSum(int[] nums, int goal) {
        if (nums==null || nums.length==0){
            return 0;
        }
        int sum=0;
        HashMap<Integer,Integer>cnt=new HashMap<>();
        int res=0;
        for(int num:nums){
            cnt.put(sum,cnt.getOrDefault(sum,0)+1);
            sum+=num;
            res+=cnt.getOrDefault(sum-goal,0);
        }

        return res;

    }
}

LeetCode 560. 和为 K 的子数组

给你一个整数数组nums和一个整数k，请你统计并返回该数组中和为k的子数组的个数。

解题思路

跟930题一致。

LeetCode 524. 和为奇数的子数组数目

给你一个整数数组arr。请你返回和为奇数的子数组数目。

由于答案可能会很大，请你将结果对10^9+7取余后返回。

解题思路

求子数组和可以通过前缀和的方式，本题中只需要维护奇数和偶数的数量，不需要维护前缀和数组。

class Solution {
    public int numOfSubarrays(int[] arr) {
        final int MODULO = 1000000007;
        int odd = 0, even = 1;
        int subarrays = 0;
        int sum = 0;
        int length = arr.length;
        for (int i = 0; i < length; i++) {
            sum += arr[i];
            subarrays = (subarrays + (sum % 2 == 0 ? odd : even)) % MODULO;
            if (sum % 2 == 0) {
                even++;
            } else {
                odd++;
            }
        }
        return subarrays;
    }
}

LeetCode 面试题 17.05. 字母与数字

给定一个放有字母和数字的数组，找到最长的子数组，且包含的字母和数字的个数相同。

返回该子数组，若存在多个最长子数组，返回左端点下标值最小的子数组。若不存在这样的数组，返回一个空数组。

解题思路

一个子数组包含的字母和数字的个数相同，等价于该子数组包含的字母和数字的个数之差为0，可以将字母转为-1，数字转为1。问题等价于在转换后的数组中寻找元素和为0的最长子数组。

为了在转换后的数组中寻找元素和为0的子数组，可以计算转换后的数组的前缀和，如果两个下标对应的前缀和相等，则这两个下标之间的子数组的元素和为0。

使用哈希表记录每个前缀和第一次出现的下标。由于空前缀的前缀和是0且对应下标-1，因此首先将前缀和0与下标-1存入哈希表。

class Solution {
    public String[] findLongestSubarray(String[] array) {
        HashMap<Integer,Integer>map=new HashMap<>();
        map.put(0,-1);
        int sum=0;
        int maxLen=0;
        int startIndex=-1;
        int len=array.length;
        for(int i=0;i<len;i++){
            if (Character.isLetter(array[i].charAt(0))){
                sum++;
            }else{
                sum--;
            }
            if (map.containsKey(sum)){
                int index=map.get(sum);
                if (i-index>maxLen){
                    maxLen=i-index;
                    startIndex=index+1;
                }
            }else{
                map.put(sum,i);
            }
        }    
        if (maxLen == 0) {
            return new String[0];
        }
        String[] ans = new String[maxLen];
        System.arraycopy(array, startIndex, ans, 0, maxLen);
        return ans; 
    }
}