代码随想录算法训练营第十八天|235.二叉搜索树的最近公共祖先，701.二叉搜索树中的插入操作，450.删除二叉搜索树节点

235.二叉搜索树的最近公共祖先

701.二叉搜索树中的插入操作

450.删除二叉搜索树节点

235.二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
说明:

所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉搜索树中。

在二叉搜索树（BST）中找到两个节点p和q的最低公共祖先（LCA）。在二叉搜索树中，最低公共祖先的特点是它的值在p和q的值之间（包括等于p或q的情况）。如果p和q的值都小于当前节点，那么它们的公共祖先位于当前节点的左子树；如果它们的值都大于当前节点，那么它们的公共祖先位于当前节点的右子树。如果p和q分别位于当前节点的两侧，那么当前节点就是它们的最低公共祖先。

代码逻辑

首先检查当前节点是否为NULL，如果是，则返回NULL。
然后，如果p和q的值都小于当前节点的值，递归地在当前节点的左子树中查找。
如果p和q的值都大于当前节点的值，递归地在当前节点的右子树中查找。
如果上述两种情况都不满足（即当前节点的值介于p和q的值之间），说明找到了最低公共祖先，返回当前节点。

这个实现利用了BST的性质来优化搜索过程，避免了不必要的遍历。

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */

class Solution {

private:
    TreeNode* traversal(TreeNode* cur, TreeNode* p, TreeNode* q) {
        if (cur == NULL) return cur;
                                                        // 中
        if (cur->val > p->val && cur->val > q->val) {   // 左
            TreeNode* left = traversal(cur->left, p, q);
            if (left != NULL) {
                return left;
            }
        }

        if (cur->val < p->val && cur->val < q->val) {   // 右
            TreeNode* right = traversal(cur->right, p, q);
            if (right != NULL) {
                return right;
            }
        }
        return cur;
    }
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        return traversal(root, p, q);
    }
};

python

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        # 如果当前节点为空，或者p、q之一就是当前节点，则直接返回当前节点
        if not root or root == p or root == q:
            return root
        
        # 根据BST的性质在左子树或右子树中查找
        if p.val < root.val and q.val < root.val:
            # p和q都在当前节点的左侧
            return self.lowestCommonAncestor(root.left, p, q)
        elif p.val > root.val and q.val > root.val:
            # p和q都在当前节点的右侧
            return self.lowestCommonAncestor(root.right, p, q)
        else:
            # 当前节点就是p和q的最低公共祖先
            return root

迭代法

在二叉搜索树（BST）中查找两个节点的最低公共祖先（LCA）时，可以使用迭代法代替递归来减少空间复杂度。迭代法的核心思想是利用BST的性质：对于树中的任意节点y，如果p和q的值都小于y，则p和q都在y的左子树中；如果p和q的值都大于y，则p和q都在y的右子树中；否则，y就是p和q的最低公共祖先。

C++

#include <iostream>

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        // 当前节点初始化为根节点
        TreeNode* current = root;
        while (current) {
            // 如果p和q的值都小于当前节点的值，则在左子树中查找
            if (p->val < current->val && q->val < current->val) {
                current = current->left;
            }
            // 如果p和q的值都大于当前节点的值，则在右子树中查找
            else if (p->val > current->val && q->val > current->val) {
                current = current->right;
            }
            // 否则，当前节点就是LCA
            else {
                return current;
            }
        }
        return nullptr;
    }
};

python

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        # 当前节点初始化为根节点
        current = root
        while current:
            # 如果p和q的值都小于当前节点的值，则在左子树中查找
            if p.val < current.val and q.val < current.val:
                current = current.left
            # 如果p和q的值都大于当前节点的值，则在右子树中查找
            elif p.val > current.val and q.val > current.val:
                current = current.right
            # 否则，当前节点就是LCA
            else:
                return current
        return None

701.二叉搜索树中的插入操作

给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。返回插入后二叉搜索树的根节点。输入数据保证，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。你可以返回 任意有效的结果 。

示例 1：
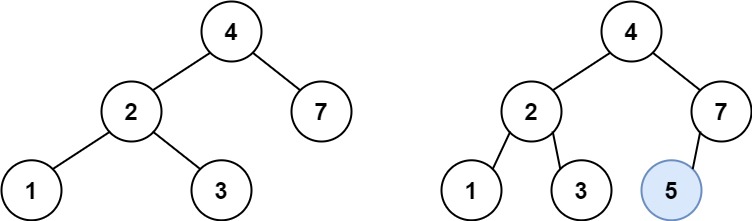
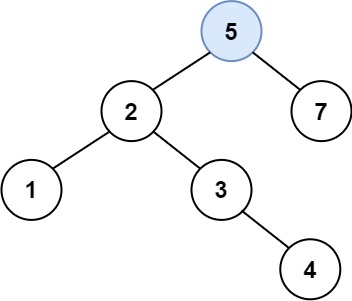
输入：root = [4,2,7,1,3], val = 5
输出：[4,2,7,1,3,5]
解释：另一个满足题目要求可以通过的树是：
示例 2：
输入：root = [40,20,60,10,30,50,70], val = 25
输出：[40,20,60,10,30,50,70,null,null,25]
示例 3：
输入：root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出：[4,2,7,1,3,5]
提示：

树中的节点数将在 [0, 104]的范围内。
-108 <= Node.val <= 108
所有值 Node.val 是 独一无二 的。
-108 <= val <= 108
保证 val 在原始BST中不存在。

将一个值插入到二叉搜索树（BST）中，并保持BST的性质。代码中使用了递归方法来找到合适的位置插入新节点。如果树为空，就直接创建一个新节点作为根节点。如果树不为空，递归遍历树直到找到合适的插入位置，然后根据值的大小插入到左子树或右子树。

代码逻辑

递归遍历：通过traversal函数递归遍历BST，parent变量用于记录当前节点的父节点，以便在找到插入位置时可以直接插入。
插入新节点：当到达空位置（cur == NULL）时，根据新节点的值与父节点的值的比较结果，决定是将新节点作为左子节点还是右子节点插入。
树为空的特殊处理：如果BST为空（root == NULL），则直接创建新节点作为根节点。

然而，原始C++代码实现中有一个潜在问题：parent变量的初始值被设置为一个新的TreeNode实例，这个实例并未被真正用作树的一部分，可能会导致内存泄漏或不必要的内存分配。在实际插入操作中，如果根节点非空，parent变量的初始值并未被使用。

C++

class Solution {
private:
    TreeNode* parent;
    void traversal(TreeNode* cur, int val) {
        if (cur == NULL) {
            TreeNode* node = new TreeNode(val);
            if (val > parent->val) parent->right = node;
            else parent->left = node;
            return;
        }
        parent = cur;
        if (cur->val > val) traversal(cur->left, val);
        if (cur->val < val) traversal(cur->right, val);
        return;
    }

public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        parent = new TreeNode(0);
        if (root == NULL) {
            root = new TreeNode(val);
        }
        traversal(root, val);
        return root;
    }
};

python

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def insertIntoBST(self, root: TreeNode, val: int) -> TreeNode:
        if not root:
            return TreeNode(val)
        
        def insert(node, val):
            if not node:
                return TreeNode(val)
            if val > node.val:
                node.right = insert(node.right, val)
            else:
                node.left = insert(node.left, val)
            return node
        
        return insert(root, val)

针对C++实现的优化主要集中在避免使用递归来降低空间复杂度，并提高代码执行效率。通过迭代方法寻找正确的插入位置

这个版本的代码使用了迭代方法来寻找新节点的正确插入位置。这种方法避免了递归调用，减少了函数调用栈的使用。
通过迭代遍历树，我们检查新值应该插入到当前节点的左侧还是右侧。如果找到一个空位置（即current->left或current->right为nullptr），就在那里插入新节点。
这种方法保持了二叉搜索树的特性，同时提高了代码的执行效率，特别是在处理大树时。

C++

#include <iostream>

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        // 如果树为空，直接创建并返回新节点作为根节点
        if (root == nullptr) {
            return new TreeNode(val);
        }
        
        // 使用迭代寻找正确的插入位置
        TreeNode* current = root; // 当前节点
        while (true) {
            // 如果插入的值大于当前节点的值
            if (val > current->val) {
                // 如果当前节点的右子节点为空，则在此位置插入新节点
                if (current->right == nullptr) {
                    current->right = new TreeNode(val);
                    break; // 插入后退出循环
                } else {
                    // 否则继续向右子树移动
                    current = current->right;
                }
            } else {
                // 如果当前节点的左子节点为空，则在此位置插入新节点
                if (current->left == nullptr) {
                    current->left = new TreeNode(val);
                    break; // 插入后退出循环
                } else {
                    // 否则继续向左子树移动
                    current = current->left;
                }
            }
        }
        
        return root; // 返回未修改的根节点
    }
};

python

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def insertIntoBST(self, root: TreeNode, val: int) -> TreeNode:
        # 如果根节点为空，直接返回新创建的节点
        if not root:
            return TreeNode(val)
        
        # 定位插入位置
        current = root
        while current:
            # 如果插入的值大于当前节点的值
            if val > current.val:
                # 如果右子节点为空，插入新节点并退出循环
                if not current.right:
                    current.right = TreeNode(val)
                    break
                # 否则，向右子树移动
                else:
                    current = current.right
            # 如果插入的值小于或等于当前节点的值
            else:
                # 如果左子节点为空，插入新节点并退出循环
                if not current.left:
                    current.left = TreeNode(val)
                    break
                # 否则，向左子树移动
                else:
                    current = current.left
        
        return root

450.删除二叉搜索树节点

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

首先找到需要删除的节点；
如果找到了，删除它。

示例 1:
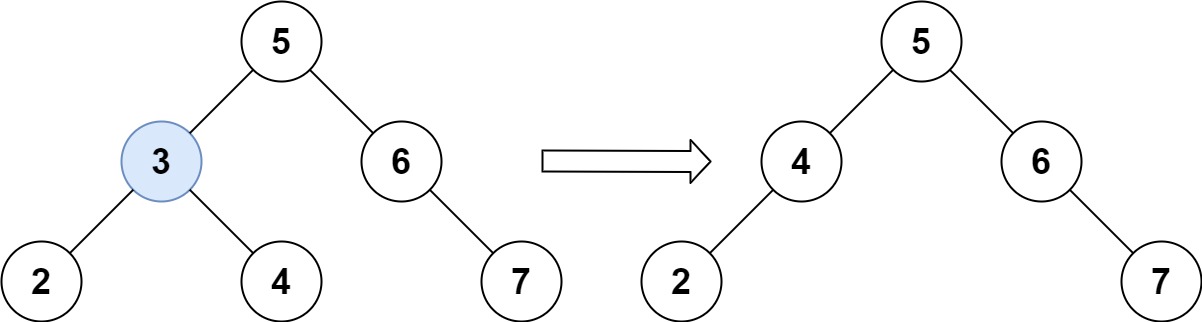
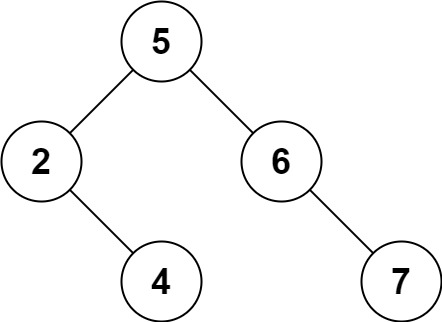
输入：root = [5,3,6,2,4,null,7], key = 3
输出：[5,4,6,2,null,null,7]
解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。
示例 2:
输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点
示例 3:
输入: root = [], key = 0
输出: []

实现了在二叉搜索树（BST）中删除一个具有特定键值的节点的功能，并且处理了多种情况，确保删除操作后，树仍然保持BST的性质。

功能分析

节点未找到：如果当前节点为空，则表示未找到要删除的节点，直接返回nullptr。
找到节点：如果找到了要删除的节点（root->val == key），根据其子节点的情况有以下几种处理方式：
- 叶子节点：如果节点是叶子节点（没有子节点），则直接删除该节点，并返回nullptr。
- 单子节点：如果节点只有一个子节点（左子节点或右子节点），则删除该节点，并用其子节点替代它，返回替代后的子节点。
- 双子节点：如果节点有两个子节点，则找到右子树中最左侧的节点（右子树中的最小节点），将要删除节点的左子树接到这个最左侧节点的左侧，然后删除节点，并用其右子节点替代它。
递归删除：如果要删除的节点值大于当前节点值，递归删除左子树中的节点；如果要删除的节点值小于当前节点值，递归删除右子树中的节点。

C++

class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if (root == nullptr) return root; // 第一种情况：没找到删除的节点，遍历到空节点直接返回了
        if (root->val == key) {
            // 第二种情况：左右孩子都为空（叶子节点），直接删除节点， 返回NULL为根节点
            if (root->left == nullptr && root->right == nullptr) {
                ///! 内存释放
                delete root;
                return nullptr;
            }
            // 第三种情况：其左孩子为空，右孩子不为空，删除节点，右孩子补位 ，返回右孩子为根节点
            else if (root->left == nullptr) {
                auto retNode = root->right;
                ///! 内存释放
                delete root;
                return retNode;
            }
            // 第四种情况：其右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点
            else if (root->right == nullptr) {
                auto retNode = root->left;
                ///! 内存释放
                delete root;
                return retNode;
            }
            // 第五种情况：左右孩子节点都不为空，则将删除节点的左子树放到删除节点的右子树的最左面节点的左孩子的位置
            // 并返回删除节点右孩子为新的根节点。
            else {
                TreeNode* cur = root->right; // 找右子树最左面的节点
                while(cur->left != nullptr) {
                    cur = cur->left;
                }
                cur->left = root->left; // 把要删除的节点（root）左子树放在cur的左孩子的位置
                TreeNode* tmp = root;   // 把root节点保存一下，下面来删除
                root = root->right;     // 返回旧root的右孩子作为新root
                delete tmp;             // 释放节点内存（这里不写也可以，但C++最好手动释放一下吧）
                return root;
            }
        }
        if (root->val > key) root->left = deleteNode(root->left, key);
        if (root->val < key) root->right = deleteNode(root->right, key);
        return root;
    }
};

python

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def deleteNode(self, root: TreeNode, key: int) -> TreeNode:
        if not root:
            return None  # 没找到删除的节点
        
        if root.val == key:
            if not root.left and not root.right:
                return None  # 叶子节点，直接删除
            elif not root.left:
                return root.right  # 只有右子节点
            elif not root.right:
                return root.left  # 只有左子节点
            else:
                cur = root.right
                while cur.left:
                    cur = cur.left  # 找到右子树最左侧的节点
                cur.left = root.left  # 将要删除节点的左子树接到cur的左侧
                return root.right  # 删除节点，返回右子节点
        
        elif root.val > key:
            root.left = self.deleteNode(root.left, key)
        else:
            root.right = self.deleteNode(root.right, key)
        
        return root

优化删除节点的代码主要关注减少代码复杂度和提高执行效率。在二叉搜索树（BST）中删除节点时，特别是当目标节点有两个子节点的情况下，一个常见的优化方法是寻找目标节点右子树的最小节点（或左子树的最大节点），然后用它来替代目标节点的值，并在该子树中递归删除那个替代的节点。这种方法避免了直接操作树的结构，只需修改节点的值，简化了节点替换的逻辑。

C++

#include <iostream>

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if (!root) return nullptr;

        if (root->val == key) {
            if (!root->left) return root->right;
            if (!root->right) return root->left;
            TreeNode* minNode = root->right;
            while (minNode->left) minNode = minNode->left;
            root->val = minNode->val;  // 替换值
            root->right = deleteNode(root->right, root->val);  // 删除替代节点
        } else if (root->val > key) {
            root->left = deleteNode(root->left, key);
        } else {
            root->right = deleteNode(root->right, key);
        }

        return root;
    }
};

python

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def deleteNode(self, root: TreeNode, key: int) -> TreeNode:
        if not root:
            return None

        if root.val == key:
            if not root.left:  # 只有右子节点或无子节点
                return root.right
            if not root.right:  # 只有左子节点
                return root.left
            # 有两个子节点，找右子树的最小节点替代删除节点
            minNode = root.right
            while minNode.left:
                minNode = minNode.left
            root.val = minNode.val  # 替换值
            root.right = self.deleteNode(root.right, root.val)  # 删除替代节点
        elif root.val > key:
            root.left = self.deleteNode(root.left, key)
        else:
            root.right = self.deleteNode(root.right, key)
        
        return root