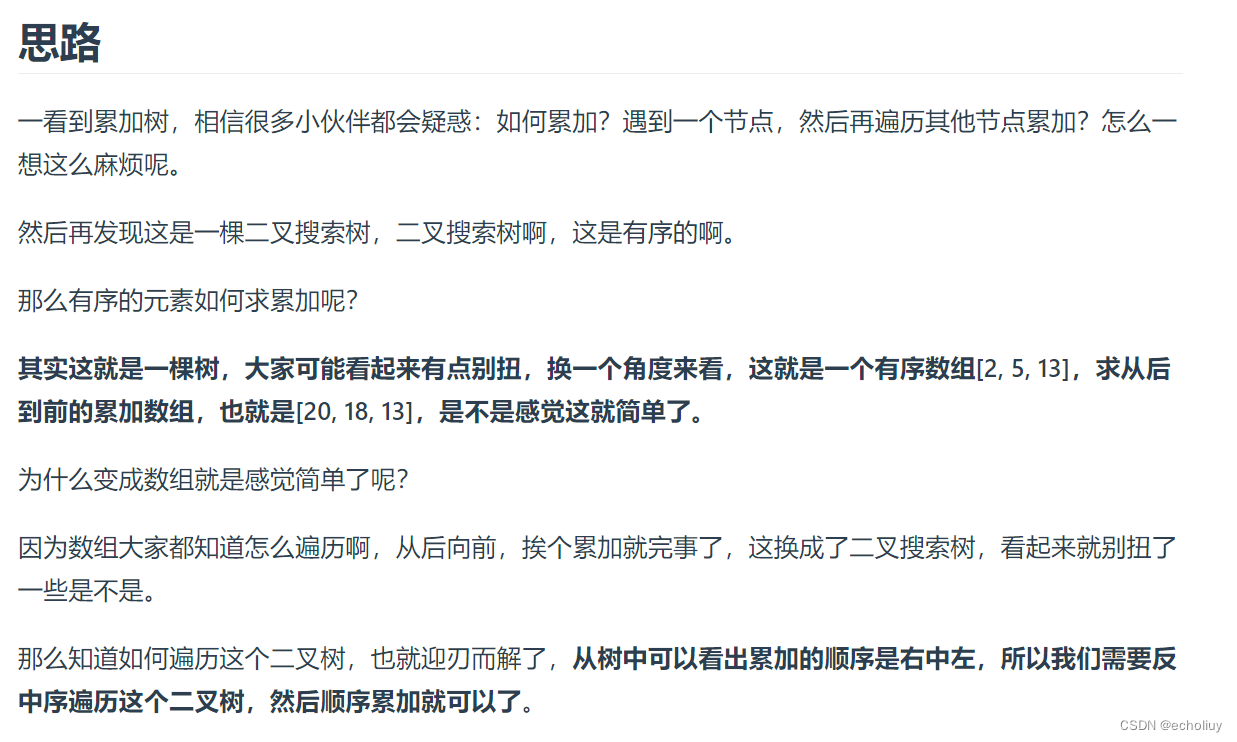
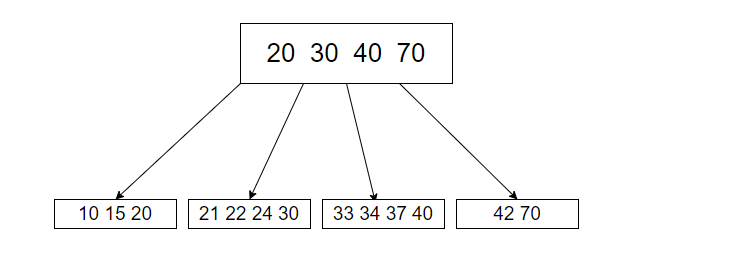
决策树是发现自变量（特征）之间交互关系的强大工具。在遍历路径中一起出现的变量是相互交互的，因为子节点的条件取决于父节点的条件。例如，在下图中，红色突出显示的路径包含三个变量：$x_1$、$x_7$ 和 $x_{10}$，因此突出显示的预测值（在突出显示的叶节点处）是 $x_1$、$x_7$ 和 $x_{10}$ 之间交互的产物。

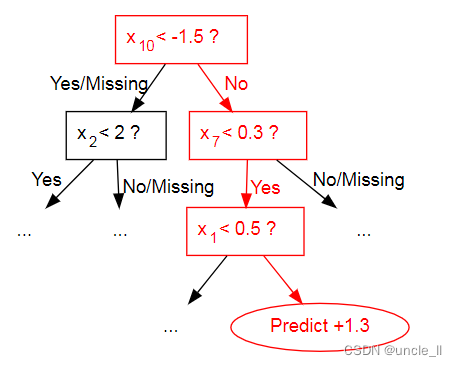
当树的深度大于1时，许多变量仅基于最小化训练损失相互作用，导致的决策树可能捕捉到虚假关系（噪音），而不是跨不同数据集泛化的合法关系。特征交互约束允许用户决定哪些变量可以相互作用，哪些不能。

潜在的好处包括：

• 通过专业领域知识或对交互作用进行排名的算法，更好的预测性能
• 预测中更少的噪音；更好的泛化效果
• 用户对模型能够拟合的内容有更多控制。例如，用户可能希望排除一些交互作用，即使它们表现良好，也受到监管约束的影响。

简单示例

特征交互约束以允许相互作用的变量组的形式表达。例如，约束[0, 1]表示变量$x_0$和$x_1$
允许相互作用，但不能与其他变量相互作用。类似地，[2, 3, 4]表示 , $x_2,x_3$和 $x_4$
可以相互作用，但不能与其他变量相互作用。一组特征交互约束表示为一个嵌套列表，例如[[0, 1], [2, 3, 4]]，其中每个内部列表是允许相互作用的特征的索引组。

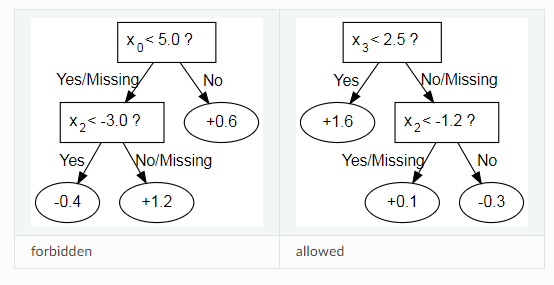
在下图中，左侧的决策树违反了第一个约束（[0, 1]），而右侧的决策树遵守了第一个和第二个约束（[0, 1]，[2, 3, 4]）。

在 XGBoost 中实施特征交互约束

强制执行特征交互约束在XGBoost中非常简单。在这里，将使用Python给出一个示例，但相同的思想可以推广到其他平台。

假设以下代码适应模型而没有特征交互约束：

model_no_constraints = xgb.train(
    params,
    dtrain,
    num_boost_round=1000,
    evals=evallist,
    early_stopping_rounds=10)

然后，仅需要添加一个参数即可使用特征交互约束进行拟合：

params_constrained = params.copy()
# Use nested list to define feature interaction constraints
params_constrained['interaction_constraints'] = '[[0, 2], [1, 3, 4], [5, 6]]'
# Features 0 and 2 are allowed to interact with each other but with no other feature
# Features 1, 3, 4 are allowed to interact with one another but with no other feature
# Features 5 and 6 are allowed to interact with each other but with no other feature

model_with_constraints = xgb.train(
    params_constrained,
    dtrain,
    num_boost_round=1000,
    evals=evallist,
    early_stopping_rounds=10)

使用特征名称代替

XGBoost的Python包支持使用特征名称而不是特征索引来指定约束条件。假设你有一个包含列["f0", "f1", "f2"]的数据框，可以将特征交互约束指定为[["f0", "f2"]]。

高级主题

交互约束背后的直觉很简单。用户可能对不同特征之间的关系有先验知识，并在模型构建过程中将其编码为约束。但在指定约束方面也有一些微妙之处。以约束[[1, 2], [2, 3, 4]]为例。第二个特征出现在两个不同的交互集中，[1, 2]和[2, 3, 4]。因此，与2允许互动的特征的并集是{1, 3, 4}。在以下图表中，根在特征2处分裂。因为所有后代都应该能够与它互动，所以在第二层，所有4个特征都是合法的分裂候选项。乍一看，这可能看起来像是忽略了指定的约束集，但实际上并非如此。

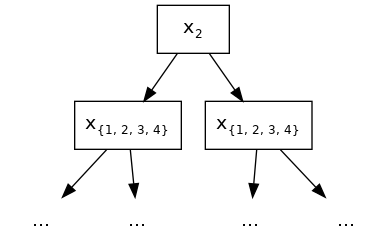
{1,2,3,4}表示合法的分割特征集。

这导致了特征交互约束的一些有趣影响。以[[0, 1], [0, 1, 2], [1, 2]]为例。假设训练数据集中只有3个可用特征以便演示，仔细的读者可能已经发现上述约束与简单的[[0, 1, 2]]相同。因为无论选择哪个特征进行根节点的分裂，所有后代都被允许将每个特征作为合法的分裂候选项，而不违反交互约束。

最后一个例子，使用[[0, 1], [1, 3, 4]]，并选择特征0作为根节点的分裂。在构建树的第二层，1是唯一的合法分裂候选项，除了0本身，因为它们属于相同的约束集。根据我们示例树的生长路径，第二层的节点在特征1处分裂。但由于1也属于第二个约束集[1, 3, 4]，在第三层，允许将所有特征包括为分裂候选项，仍然符合其祖先的交互约束。

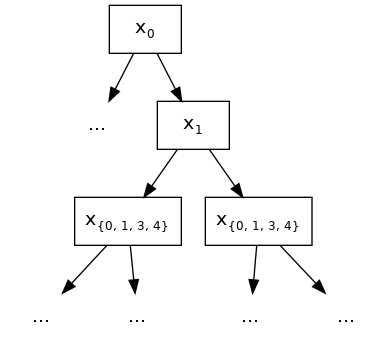
{0, 1, 3, 4} 表示合法分割特征的集合。

参考

• https://xgboost.readthedocs.io/en/latest/tutorials/feature_interaction_constraint.html