题目

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 ：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图。
在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 

思路：

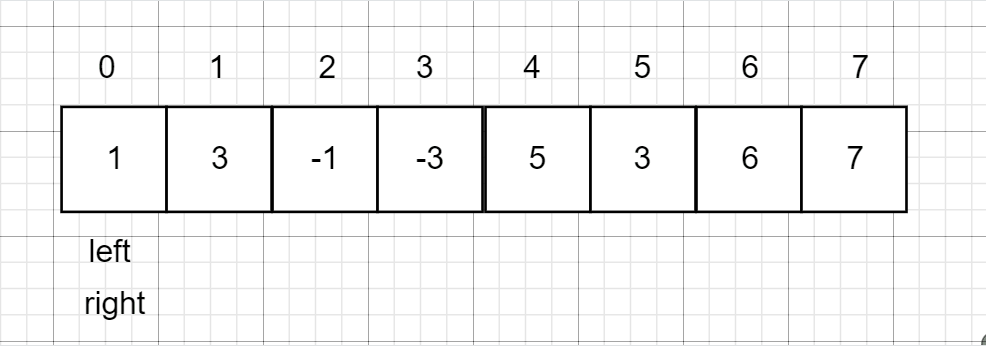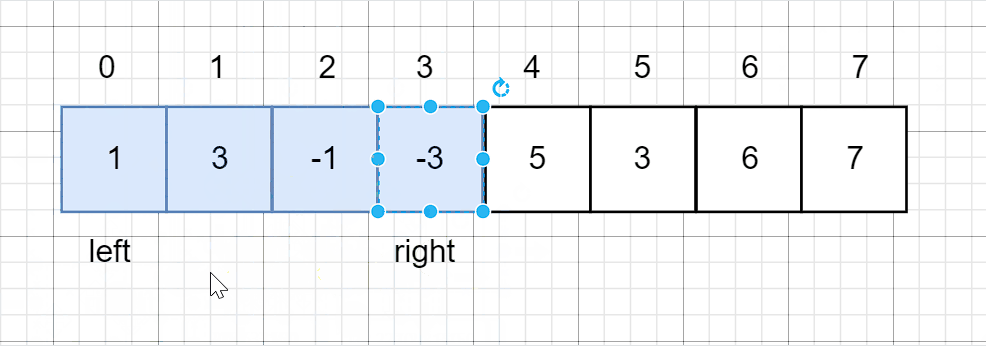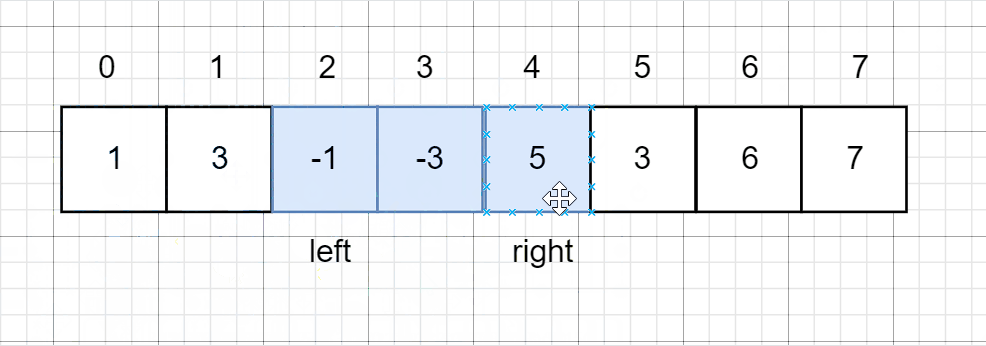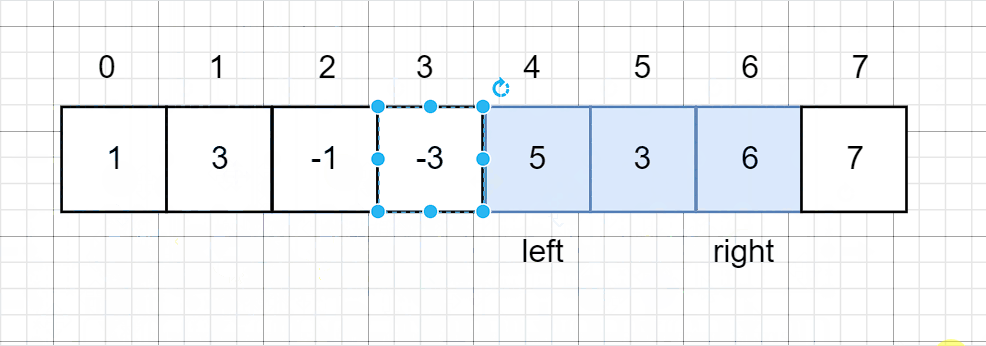
从题目中我们可以知道：只有凹陷的地方才可以存储雨水，那么高度一定是先减后增，所以当我们遍历到增这个位置时，前面减的地方（即凹陷的地方）一定会存储雨水，这时我们将凹陷处出栈就可以计算它能存储的雨水量了。
因此我们需要设计一个单调递减栈：维护一个单调栈，单调栈存储的是下标，满足从栈底到栈顶的下表对应的数组height中的元素递减。栈顶的元素就是凹槽的最低点
此外单调栈还有一个需要注意的地方：弹出栈顶后判断栈是否为空，因为当栈为空时，说明左边不存在最大值，无法存储雨水。

Code：

class Solution {
public:
    int trap(vector<int>& height) {
        if(height.size() <= 1)
        {
            return 0;
        }
        stack<int>st;
        int sum=0;
        st.push(0);
        for(int i=1 ; i < height.size() ; i++)
        {
            while(!st.empty() && height[i] > height[st.top()])
            {
                int vis = st.top();
                st.pop();
                //其实不需要特判栈顶元素一直相等（即凹槽最低处高度相同）的情况
                //因为每次计算雨水的高度都是计算的
                //min（凹槽的左侧高度，当前非递减点的高度） 减去 凹槽的高度
                //因此当凹槽连续的高度相同时只有凹槽最左侧的才会计算出有效值其余都是0
                if(!st.empty())
                {
                    int l = i - st.top() -1;
                    int h = min(height[i] , height[st.top()]) - height[vis];
                    sum += l*h;
                }
            }
            st.push(i);
        }
        return sum;
    }
};