单调队列和优先队列

news2024/11/24 6:04:22

本篇记录下一下关于单调队列和优先队列（堆）的方法以及解题思路.

文章目录

  • 一. 单调队列
    • 1. 绝对差不超过限制得最长连续子数组
    • 2. 跳跃游戏 VI
    • 3. 设计自助结算系统
    • 4. 和至少为k的最短子数组
    • 5. 满足不等式的最大值
  • 二. 优先队列
    • 1. 最后一块石头的重量
    • 2. 数据流中的第k大元素
    • 3. 拼车
      • （1）前缀和
      • （2）优先队列（堆）
    • 4. 滑动窗口最大值
      • （1）单调队列
      • （2）优先队列

一. 单调队列

1. 绝对差不超过限制得最长连续子数组

在这里插入图片描述
这道题是要求我们求出连续子数组中最大值和最小值差，差小于等于所给的limit。
然后返回连续子数组最大的长度。

  1. 找出子数组中最大值和最小值
  2. 两值相减去，小于等于limt，取其长度，选择那个最长的。

所以我们可以利用两个指针锁定窗口，也即是长度，然后在窗口中更新不断的更新最大值和最小值。

  • 所以我们可以维护两个单调增减队列，使队首永远是最大值或者最小值。
  • 当窗口中最大值 - 最小值 > limit 时候就需要修改窗口大小，使left++
  • 如果说nums[left] 这个值呢正好就是最大值或者最小值，那么相应的它也得出队列。
#define MAX_SIZE 100000

int Max(int x , int y)
{
    return x > y ? x : y;
}

int longestSubarray(int* nums, int numsSize, int limit) 
{
    //增减单调队列
    int* deQueue = (int*)malloc(sizeof(int) * MAX_SIZE);
    int* inQueue = (int*)malloc(sizeof(int) * MAX_SIZE);
    int deFront = 0, deRear = 0, inFront = 0, inRear = 0;
    //
    int left = 0, right = 0, result = 0;
    while(right < numsSize)
    {
        //维护单调递减队列
        while(deFront < deRear && deQueue[deRear - 1] < nums[right])
        {
            deRear--;
        }

        //维护单调递增队列
        while(inFront < inRear && inQueue[inRear - 1] > nums[right])
        {
            inRear--;
        }

        //入队列
        deQueue[deRear++] = nums[right];
        inQueue[inRear++] = nums[right++];

        while(deFront < deRear && inFront < inRear && deQueue[deFront] - inQueue[inFront] > limit)
        {
            //修改窗口大小，即left往前。
            //对于两个队列来说，如果删除的left 是当前窗口的最大值或者最小值，那么相对应得队首也得删除
            if(deQueue[deFront] == nums[left])
            {
                deFront++;
            }
            if(inQueue[inFront] == nums[left])
            {
                inFront++;
            }
            left++;
        }

        //更新窗口大小 取最大值
        result = Max(result, right - left);
    }

    return result;
}

2. 跳跃游戏 VI

在这里插入图片描述
这道题也是要求我们从0下标位置开始，然后跳k步，返回经过之和的最大值。
说白了就是说，在给定的k窗口大小中，找出从0起点位置，和窗口中各个数据总和的最大值，然后让那个数成为了新的起点，接着运算。

  • 需要一个dp数组和单调队列来实现整个代码。
  • dp数组里面存放的是和，队列中存储的下标，而下标所对应的dp一定是递增的，保证越来越大，这样子才可以使最后的结果越来越大。

在整个遍历数组的过程中，对于每个数据分为三个步骤。

  1. 首先判断当前的窗口大小是否满足 k，又因为使单调增队列，所以将队首更新成下一个就好了。
  2. 接下来就是算出当前的dp[i]，也就是front + nums[i]的值。
  3. 算出当前的dp[i]后，需要保证队列是单调增的，所以如果发现队尾的数据和当前的dp不满足单调增时候，需要将队尾进行出队操作。
int maxResult(int* nums, int numsSize, int k)
{
    int* dp = (int*)malloc(sizeof(int) * numsSize);
    int* queue = (int*)malloc(sizeof(int) * numsSize);
    int front = 0, rear = 0;
    
    //dp数组存放的最大的分数
    dp[0] = nums[0];
    //队列中，队首永远会是当前的最优解，整个队列也是呈递增的。
    queue[rear++] = 0;

    for (int i = 1; i < numsSize; i++)
    {
        //最多可以跳K步，判断是否需要收缩窗口大小
        if(front < rear && queue[front] < i - k)
        {
            front++;
        }
        
        //dp
        dp[i] = dp[queue[front]] + nums[i];

        //维护单调队列
        while(front < rear && dp[queue[rear - 1]] <= dp[i])
        {
            rear--;
        }
        //入队列
        queue[rear++] = i;
    }


    return dp[numsSize - 1];
}

3. 设计自助结算系统

在这里插入图片描述
这道题其实就是要求我们设计一个队列出来，遵循现进先出的原则，但是在此基础上增加了一个要求，就是获取最大值的要求，你可以遍历整个队列获取，但是不符合题，题目中要求是O（1）.
所以我们可以维护一个单调递减的队列出来，这样就可以保证说这个递减队列的队首位置永远是最大的。
这道题和栈中的设计一个最小栈题目是很类似的，那道题目是设计两个栈，而这一道是设计两个队列。

#define MAX_SIZE 10000



typedef struct
{
    int* queue;     //正常队列，待结算的商品
    int* deQueue;   //单调递减队列，也就是说队首永远是最大的待结商品
    int front,rear,deFront,deRear;
} Checkout;


Checkout* checkoutCreate()
{
    Checkout* obj = (Checkout*)malloc(sizeof(Checkout));
    obj -> queue = (int*)malloc(sizeof(int) * MAX_SIZE);
    obj -> deQueue = (int*)malloc(sizeof(int) * MAX_SIZE);
    obj -> front = obj -> rear = obj -> deFront = obj -> deRear = 0;


    return obj;
}

int checkoutGet_max(Checkout* obj)
{
    if(obj -> front == obj -> rear)
    {
        //队列为空
        return -1;
    }

    //递减队列的队首
    return obj -> deQueue[obj -> deFront];
}

void checkoutAdd(Checkout* obj, int value)
{
    //入正常队列
    obj -> queue[(obj -> rear)++] = value; 

    //入单调递减队列
    while(obj -> deFront != obj -> deRear && obj -> deQueue[obj -> deRear - 1] < value)
    {
        obj -> deRear--;
    }
    obj -> deQueue[(obj -> deRear)++] = value;
}

int checkoutRemove(Checkout* obj)
{
    if(obj -> front == obj -> rear)
    {
        //队列为空
        return -1;
    }


    if(obj -> queue[obj -> front] == obj -> deQueue[obj -> deFront])
    {
        //同时出队列
        obj -> deFront++;
    }
    return obj -> queue[(obj -> front)++];
}

void checkoutFree(Checkout* obj)
{
    free(obj -> queue);
    free(obj -> deQueue);
    free(obj);    
}

/**
 * Your Checkout struct will be instantiated and called as such:
 * Checkout* obj = checkoutCreate();
 * int param_1 = checkoutGet_max(obj);
 
 * checkoutAdd(obj, value);
 
 * int param_3 = checkoutRemove(obj);
 
 * checkoutFree(obj);
*/

4. 和至少为k的最短子数组

在这里插入图片描述
这道题要求我们求出连续的子数组的和最少是k的最短长度是多少。
经典的滑动窗口 + 单调队列的解法。

  • 这道题需要反复的取求数组的和，所以我们先预处理一下前缀和数组。
  • 当求出前缀和数组后，知道一些基本的道理有助于下面的运算。
  • 一下这个公式应该都会吧，

给一个前缀和数组 prefixSum, 然后 i < j
pre[i] = nums[0] + nums[1] + nums[2] + nums[i].
pre[j] = nums[0] + nums[1] + nums[2] + nums[i] + nums[i + 1] +…+ nums[j]
pre[i,j] = pre[j] - pre[i].

  • i 和 j 其实就是滑动窗口中的左右边界。
  • 当 i ~ j 的和求出来后，发现和大于等与k的话。
  • 我们可以计算出该窗口的长度 i - j;
  • 同时缩小窗口大小。
  • 如果没有大于等于k,我们继续扩大窗口的大小。
    下图是滑窗口简单的运算过程:举例有点特殊，k是6，所以一直在不断的更新

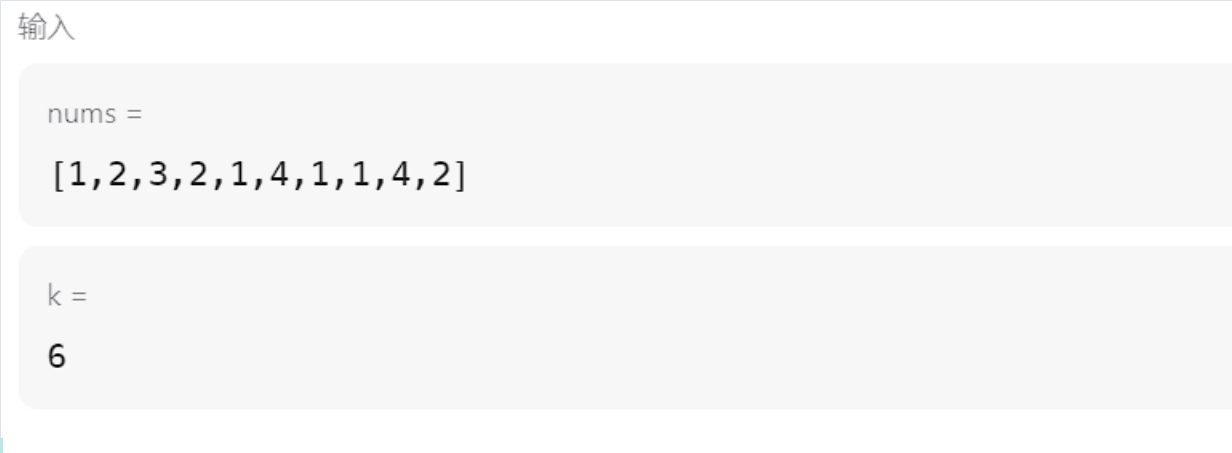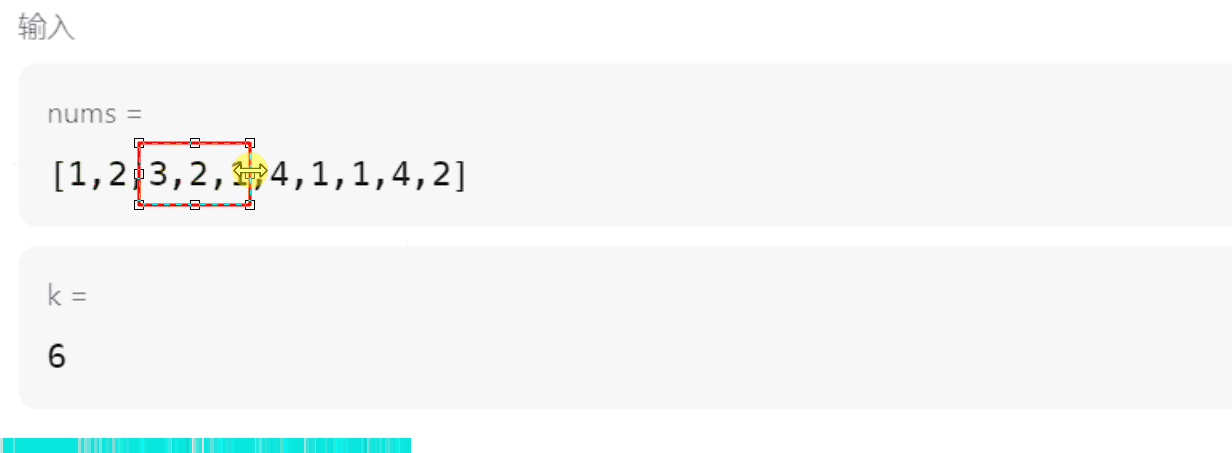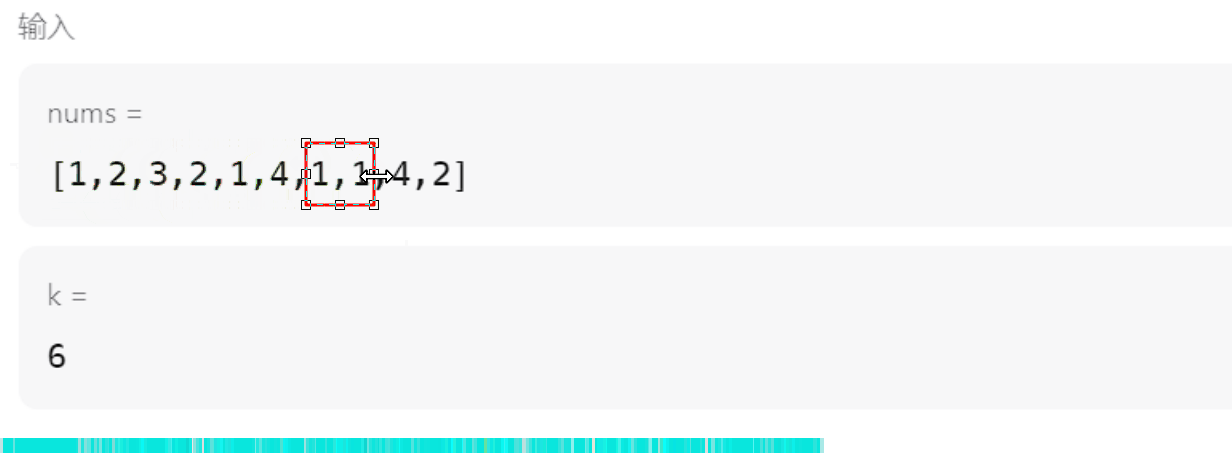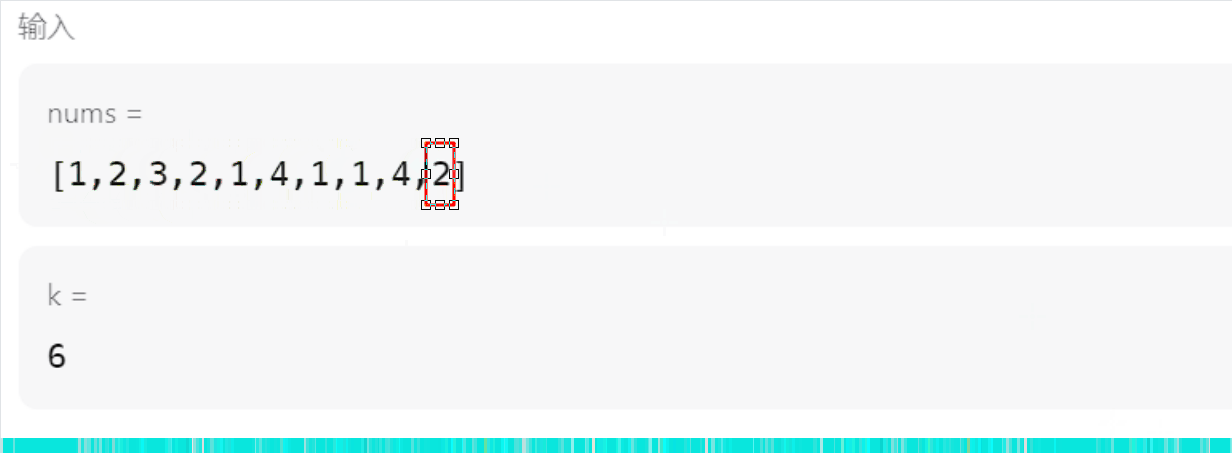
在这里插入图片描述

  • 但是这个不就是用双指针就可以做到吗？为什么需要优先队列，因为还有一个细节需要注意。
  • 我们在遍历nums数组的时候，必须保证前缀和是单调递增的，
  • 如果发现当前的前缀和比队尾前缀和小，那么我们就将当前的变成新的队尾
  • 看下下面的例子，当只是用滑动窗口处理这道题的时候，最后的结果一定是4，也就是整个数组的和35,窗口的大小是从0到4.（绿色）
  • 但是呢，发现15+15=30长度为2，2才是最后的答案，所以前缀和数组中收0 2 3的方式，因为prefix[2] < prefix[1] ,将其更换掉了。
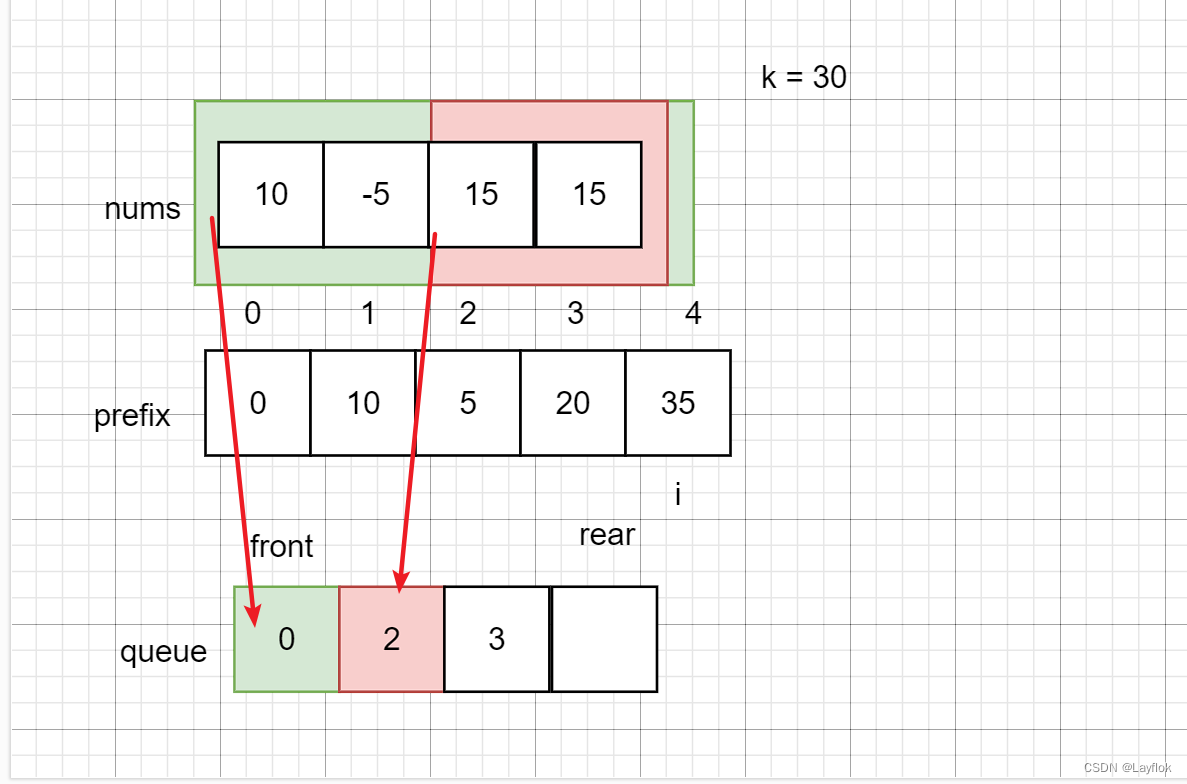
    在这里插入图片描述
int Min(int x, int y)
{
    return x < y ? x : y;
}


int shortestSubarray(int* nums, int numsSize, int k)
{
    int n = numsSize, i;
    
    //前缀和
    long long* prefixSum = (long long*)malloc(sizeof(long long) * (n + 1));
    prefixSum[0] = 0;
    for (i = 1; i <= n; i++)
    {
        prefixSum[i] = prefixSum[i - 1] + nums[i - 1];
    }

    //递增队列，队列中存储的是前i个的前缀和 queue[i]。
    int* dequeue = (int*)malloc(sizeof(int) * (n + 1));
    int front = 0, rear = 0;
    dequeue[rear++] = 0;    //初始化，也就是前0个的前缀和。
    
    int ans = n + 1;
    for (i = 1; i <= n; i++)
    {
        //判断是否需要更新窗口大小，left,左边的窗口
        while (front != rear && prefixSum[i] - prefixSum[dequeue[front]] >= k)
        {   
            ans = Min(ans,i - dequeue[front]);
            front++;
        }

        //维护单调队列，保证队列中下标所存储的前缀和是递增的.
        while (front != rear && prefixSum[i] <= prefixSum[dequeue[rear - 1]])
        {
            rear--;
        }

        dequeue[rear++] = i;
    }

    return ans == n + 1 ? - 1 : ans;
}

5. 满足不等式的最大值

在这里插入图片描述
这道题是要求我们在一个范围，按公式求值，返回最大的那个值。
范围就是| xi - xj | <= k. 公式是：yi + yj + | xi - xj |.

对公式简单的进行推导一下：
既然说题目中说了是升序排列，所以一定有i < j。
那么|xi - xj| 可以变换成 xj - xi。
yi + yj + xj - xi = (xj + yj) + (yi - xi)的形式

  • 有了上面新的公式后呢，我们规定（xj + yj）为新节点，（yi - xi）为队列中存储的节点。
  • 那么要想使此式子变大，新节点大小不可控，遍历到什么使什么，但是（yi - xi）既然使遍历过的节点，存放在队列中的，那么我们可以在存放的时候，就选择越来越大的存放，不用讲小的存进去，就好了。

对于整体的数组遍历可分成一下几种步骤:

  1. 判断窗口大小是否符合，队首即窗口left
  2. 更新ans，利用这个公式去更新(xj + yj) + (yi - xi)。
  3. 维护队列，使队列成一个单调递增的形式，越来越大的，用当前(yi - xi)和队尾的进行比较。
int Max(int x, int y)
{
    return x > y ? x : y;
}


int findMaxValueOfEquation(int **points, int pointsSize, int *pointsColSize, int k)
{
    int* queue = (int*)malloc(sizeof(int) * pointsSize);
    int front = 0, rear = 0;
    int ans = INT_MIN;
    queue[rear++] = 0;
    for (int i = 1; i < pointsSize; i++)
    {
        //先判断窗口大小是否符合
        while(front != rear && points[i][0] - points[queue[front]][0] > k)
        {
            front++;
        }

        if(front != rear)
        {
            //队列不为空则尝试更新ans
            //(xj + yj) + (yi - xi)
            ans = Max(ans,points[i][0] + points[i][1] + points[queue[front]][1] - points[queue[front]][0]);
        }

        //维护单调递增队列，使队尾永远保持大的值。
        //判断那一个的 yi - xi 更大 
        while(front != rear && points[queue[rear - 1]][1] - points[queue[rear - 1]][0] <= points[i][1] - points[i][0])
        {
            rear--;
        }

        //push
        queue[rear++] = i;
    }
    free(queue);
    return ans;
}

二. 优先队列

1. 最后一块石头的重量

在这里插入图片描述
这道题目要求我们每次从数组中选择出两个最大值，如果他俩相等抵消，否则的话就将差入再入数组，最后返回仅省一个石头的重量，也可以没有石头（return 0）.

  • 这道题我们肯定能使用排序来做，选出两个最大值后，判断是否需要插入差值。
  • 然后再进行排序，直到数组中的元素不够两个时候。
  • 我们可以在此思想上进一步优化优化一下，不用对数组每个元素都进行排序。
  • 我们理由优先队列（堆），建立一个大顶堆，是堆的首元素永远是最大的。
  • 然后对其进行相应的出队列，入队列即可。
void Swap(int* x, int* y)
{
    int tmp = *x;
    *x = *y;
    *y = tmp;
}

//维护堆
void Heapify(int* nums, int numsSize, int i)
{
    int maxIndex = i, lc = 2 * i + 1, rc = 2 * i + 2;
    if (lc < numsSize && nums[lc] > nums[maxIndex])
    {
        maxIndex = lc;
    }
    if (rc < numsSize && nums[rc] > nums[maxIndex])
    {
        maxIndex = rc;
    }
    if (maxIndex != i)
    {
        Swap(&nums[maxIndex], &nums[i]);
        Heapify(nums, numsSize, maxIndex);
    }
}

//将val插入堆中去
void HeapPush(int* nums, int* numsSize, int val)
{
    //在最后面插入
    nums[(*numsSize)++] = val;
    //维护当前插入后的父亲节点
    for (int parent = (*numsSize - 2) / 2; parent >= 0; parent = (parent - 1) / 2)
    {
        Heapify(nums, *numsSize, parent);
        //最后一次
        if (parent == 0)
        {
            break;
        }
    }
}

//删除堆顶元素
void HeapPop(int* nums, int* numsSize)
{
    //将堆顶元素和最后一个交换
    Swap(&nums[0], &nums[--(*numsSize)]);
    //重新维护堆
    Heapify(nums, *numsSize, 0);
}

int lastStoneWeight(int* stones, int stonesSize)
{
    if (stonesSize == 1)
    {
        return stones[0];
    }

    if (stonesSize == 2)
    {
        return abs(stones[0] - stones[1]);
    }

    int i, n = stonesSize;
    //创建堆
    for (i = (n - 1) / 2; i >= 0; i--)
    {
        Heapify(stones, n, i);
    }
    while (n >= 2)
    {
        //获取两次堆顶的元素
        int x = stones[0];
        HeapPop(stones, &n);
        int y = stones[0];
        HeapPop(stones, &n);

        //如果两次不一样，那么相减后入堆
        if (x > y)
        {
            HeapPush(stones, &n, x - y);
        }
    }

    //堆为空的话，说明抵消没了。
    return n == 0 ? 0 : stones[0];
}

下面是对上述代码中的所提到堆函数进行简单的一些讲解：
堆这种数据结构是二叉树的一种形式，其在数组中存放，实现起来还是挺方便的。
下面简单的讲一下heap函数中一些细节。

  • Pop： 删除堆顶元素，其实就跟堆排序一样，将堆顶数据和最后一个交换，然后size减小，重新维护堆顶就好了。
  • Push：插入元素，这个有些细节需要注意，在当前队列（堆）得末尾直接插入元素，同样也是需要进行维护的，在数组中存储二叉树，我们可以用利用下标直接得到父亲节点和左右孩子。
  • 对于我上面的是根节点存放在0下标的位置，
  • 已知parent = i， leftchild = 2 * i + 1, rightChild = 2 * i + 2;
  • 已知（左右通用）child = i，parent = （i - 1） / 2;
    还有一种是根节点存放在1号索引处是又一种方式，这里就不仔细说了。

2. 数据流中的第k大元素

在这里插入图片描述
这道题要求我们设计一种数据结构，可以返回第k大的元素，简单来讲就是说给你一个数组，然后对其进行降序排序，第k个就是第k大的元素，用数组可以做出来，但是对于这道题目来说，时间耗费非常大，这道题可以使用堆来实现。

  • 我们来维护一个小顶堆出来，保证每次堆顶的数据都是最小的。
  • 接下来终点来了：整个堆的大小一定得是 k，那么既然大小是k，所以堆顶的元素肯定就是第k个最大的数据了，有点抽象还是看图吧：
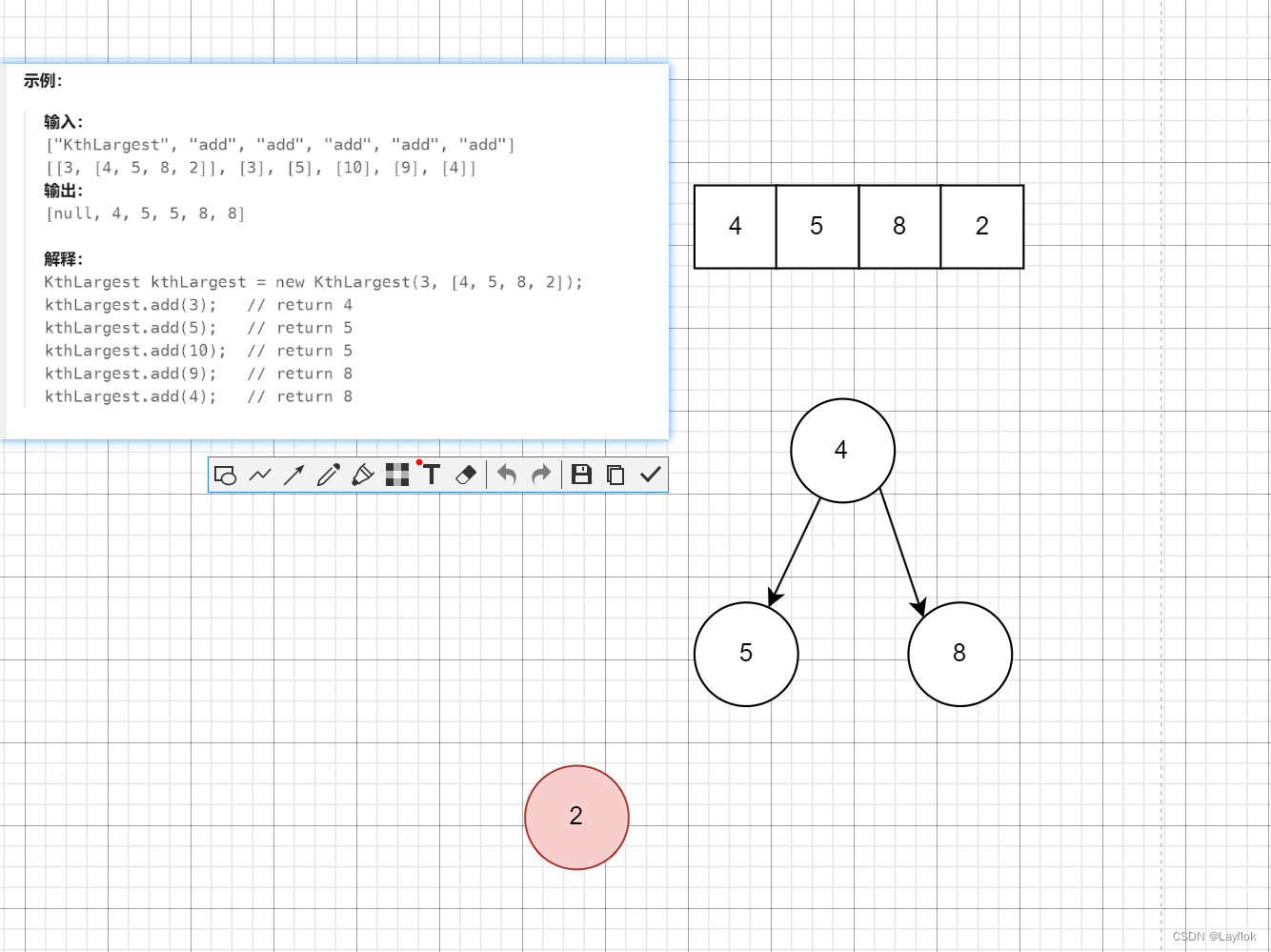
    在这里插入图片描述
    就比如上图中，nums数组大小是4，但是我们的堆中只放k个，至于是如何舍弃2的，待会再说。
  • 当后续新的数据需要add到堆中时候，如果数据比堆顶小，那么就不需要插入堆中，你插进来不会影响第k大元素，没有意义，就不插入了，
  • 相反，如果说新的数据比堆顶的大，那么将其将堆顶数据替换后，继续维护堆。
    下面是测试用例1的模拟过程：
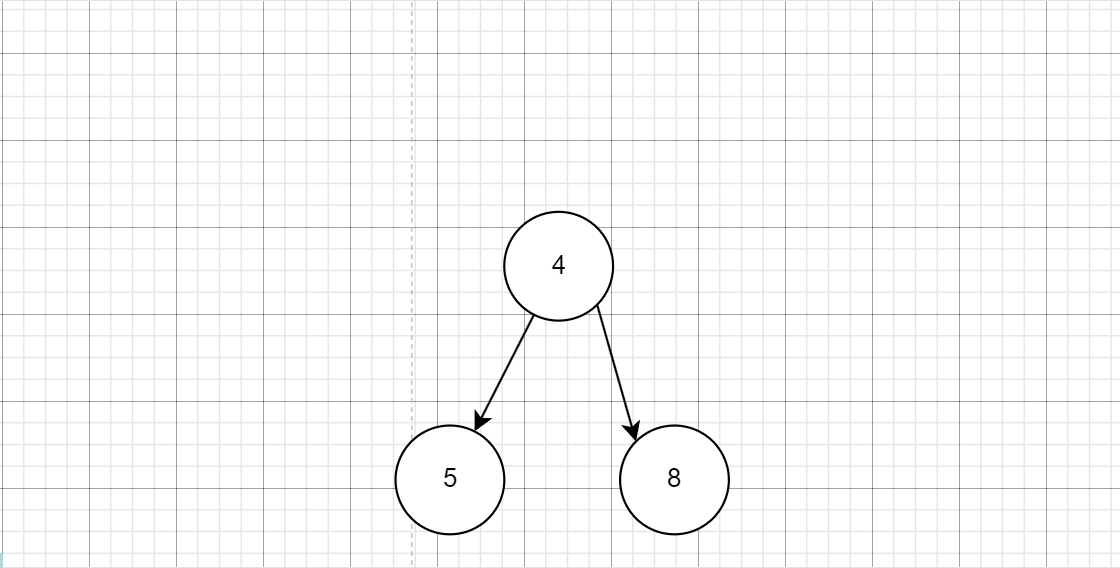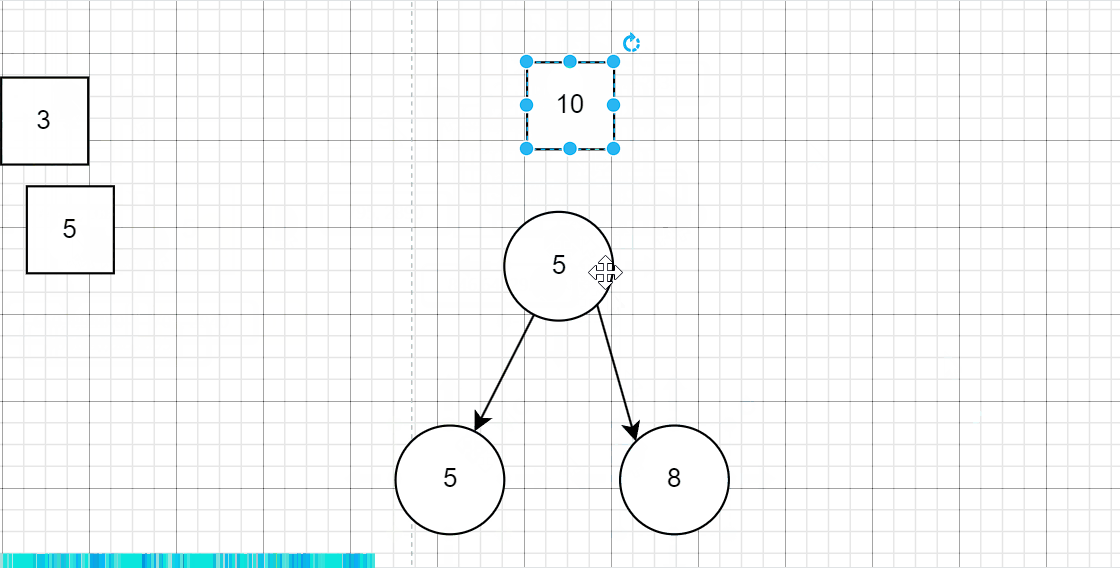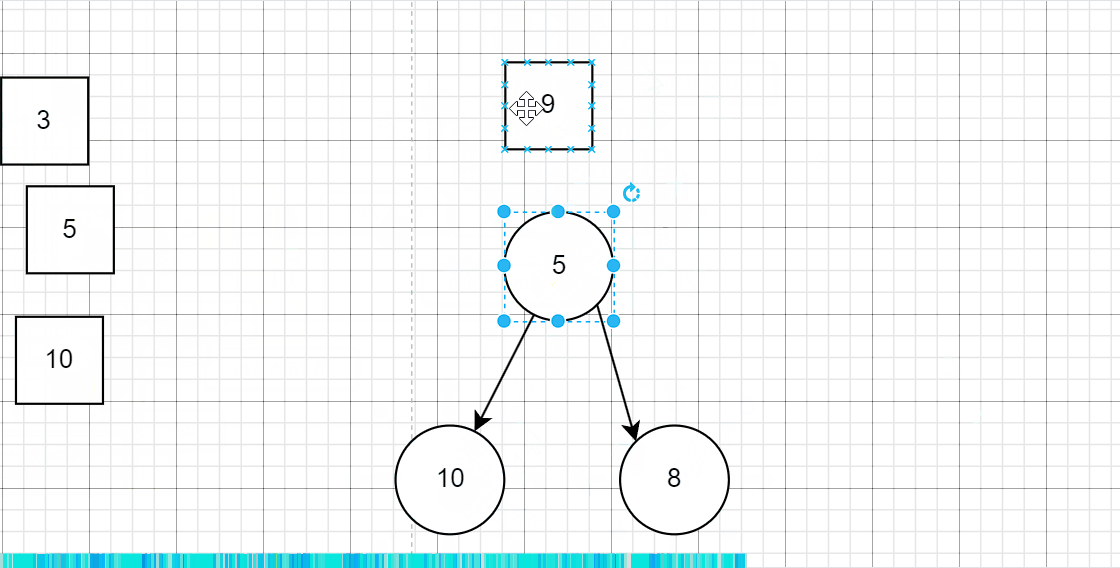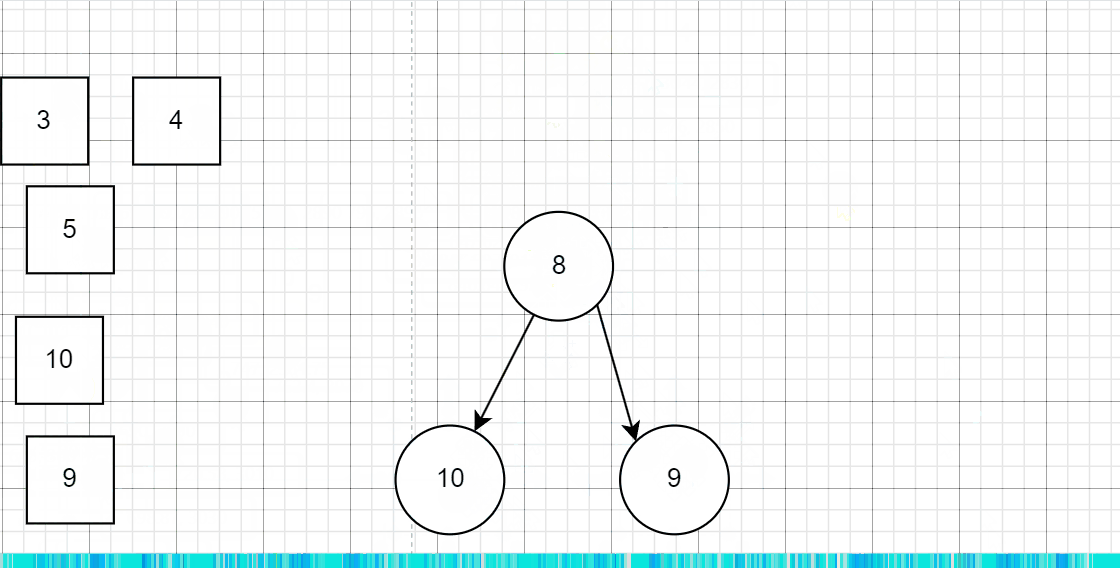
    在这里插入图片描述
    那对于刚开始的初始化堆，从刚开始初始化的时候，就选择数组中的前k个最大的就好了，如果数组中不够k个，将整个数组入堆就好了。
typedef struct
{
    int* heap;
    int capacity,k; // k是整个堆的大小，capacity 是当前堆中的元素
} KthLargest;


int cmp_int(const void* x, const void* y)
{
    return *(int*)x - *(int*)y;
}
void Swap(int* x, int* y)
{
    int tmp = *x;
    *x = *y;
    *y = tmp;
}

void Heapfiy(int* nums, int size, int i)
{
    int minIndex = i, lc = 2 * i + 1, rc = 2 * i + 2;
    if(lc < size && nums[lc] < nums[minIndex])
    {
        minIndex = lc;
    }
    if(rc < size && nums[rc] < nums[minIndex])
    {
        minIndex = rc;
    }

    if(minIndex != i)
    {
        Swap(&nums[i],&nums[minIndex]);
        Heapfiy(nums,size,minIndex);
    }
}

KthLargest* kthLargestCreate(int k, int* nums, int numsSize)
{
    KthLargest* obj = (KthLargest*)malloc(sizeof(KthLargest));
    obj -> heap = (int*)malloc(sizeof(int) * k);    //堆中最多放k个数据，然后维护一个小顶堆，堆顶就是第k个最大元素。
    int i;
    qsort(nums,numsSize,sizeof(int),cmp_int);
    if(numsSize < k)
    {
        //将数组中的所有元素入堆即可
        for (i = 0; i < numsSize; i++)
        {
            obj -> heap[i] = nums[i];
        }
        obj -> capacity = numsSize;
    }
    else
    {
        int pos = 0;
        //只入后k个
        for (i = numsSize - k; i < numsSize; i++)
        {
            obj -> heap[pos++] = nums[i];
        }
        obj -> capacity = k;
    }
    obj -> k = k;
    return obj;
}

int kthLargestAdd(KthLargest* obj, int val)
{
    
    if(obj -> capacity != obj -> k)
    {
        //需要插入堆
        obj -> heap[(obj -> capacity)++] = val;
        for (int parent = (obj -> capacity - 2) / 2; parent >= 0; parent = (parent - 1) / 2)
        {
            Heapfiy(obj -> heap,obj -> capacity, parent);
            if(parent == 0)
            {
                break;
            }
        }
        return obj -> heap[0];
    }


    if(val > obj -> heap[0])
    {
        //新元素大于堆顶则需要入堆
        obj -> heap[0] = val;
        Heapfiy(obj -> heap,obj -> capacity, 0);
    }

    return obj -> heap[0];
}

void kthLargestFree(KthLargest* obj)
{
    free(obj -> heap);
    free(obj);
}

3. 拼车

在这里插入图片描述
这道题是给我们一个二维数组，里面放着当前站上几个人，然后到哪里下。
问我们会不会超载。

（1）前缀和

  • 最直观的我们遍历一遍所给的数组，将其起点和终点的位置进行相应的赋值
  • 看下图，我在每个位置进行相应的增人减人操作
  • 那total 进行相应的自增，如果total > capacity 时候就说明超载了
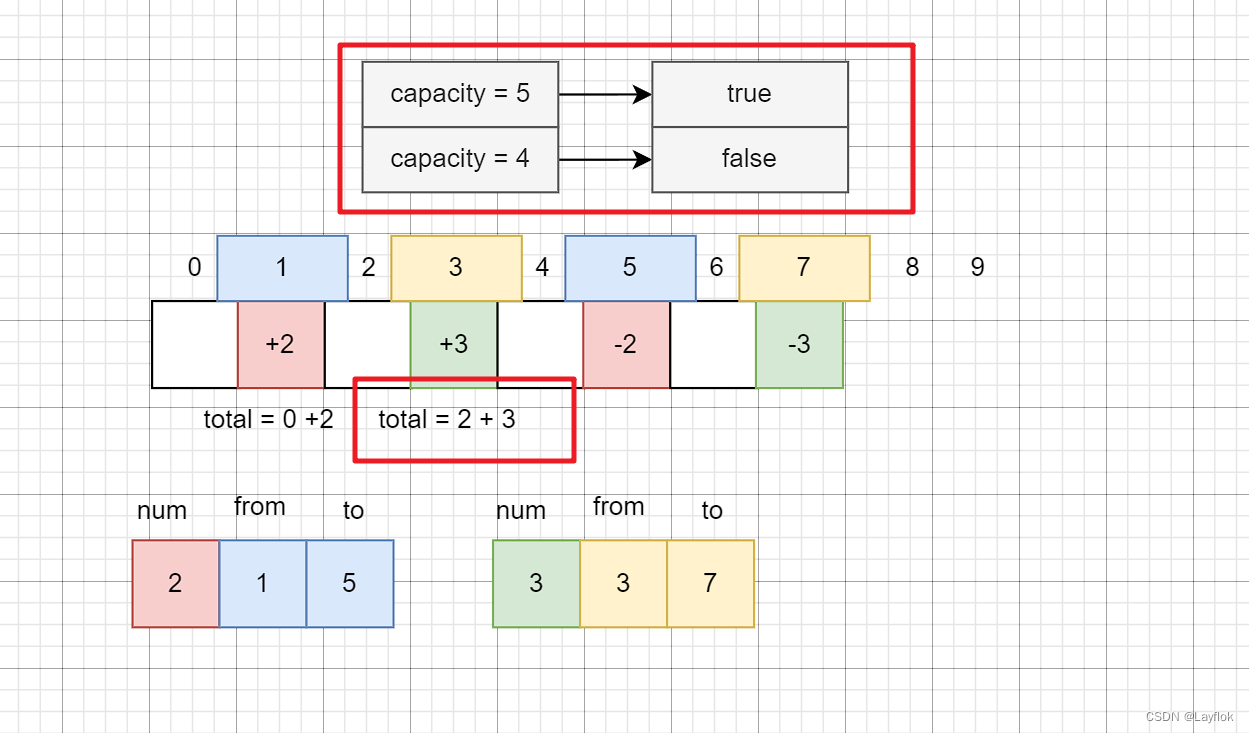
    在这里插入图片描述
    代码如下：
#define MAX_SIZE 1001

bool carPooling(int** trips, int tripsSize, int* tripsColSize, int capacity)
{
    int* bucket = (int*)malloc(sizeof(int) * MAX_SIZE);
    int i, total = 0;
    memset(bucket,0,sizeof(int) * MAX_SIZE);
    for (i = 0; i < tripsSize; i++)
    {
        int num = trips[i][0], from = trips[i][1], to = trips[i][2];
        bucket[from] += num;
        bucket[to] -= num;
    }

    for (i = 0; i < MAX_SIZE; i++)
    {
        total += bucket[i];
        if(total > capacity)
        {
            return false;
        }
    }

    return true;
}

（2）优先队列（堆）

也可以使用优先队列进行模拟实现

  • 首先对原来的数组进行排序，按照它的上车顺序进行升序排序。
  • 然后使用优先队列，其队首永远是最先下车的那批乘客。
  • 就是说最先下车的位置 <= 当前上车的位置。
  • 就将其出队列。
  • 还是如果total大于了capacity的话返回false

下面是代码思路还是比较简单的：

bool carPooling(int** trips, int tripsSize, int* tripsColSize, int capacity)
{ 
    //首先给trips 排序，使其上车起点是递增的
    qsort(trips,tripsSize,sizeof(trips[0]),cmp_from);
    int* heap = (int*)malloc(sizeof(int) * tripsSize);
    int size = 0,total = 0; //size 是堆的大小， total 是当前车上的乘客
    for (int i = 0; i < tripsSize; i++)
    {
        //最先下车的位置 <= 当前上车的位置
        while(size != 0 && trips[heap[0]][2] <= trips[i][1])
        {
            total -= trips[heap[0]][0];
            HeapPop(trips,heap,&size);
        }
        //入堆
        HeapPush(trips,heap,&size,i);
        total += trips[i][0];
        if(total > capacity)
        {
            return false;
        }
    }

    return true;
}

C语言需要自己实现一下堆.

//因为堆中存储的是下标，需要将trips整个数组传过来。
void Heapfiy(int** trips, int* nums, int size, int i)
{
    int minIndex = i, lc = 2 * i + 1, rc = 2 * i + 2;
    if(lc < size && trips[nums[lc]][2] < trips[nums[minIndex]][2])
    {
        minIndex = lc;
    }
    if(rc < size && trips[nums[rc]][2] < trips[nums[minIndex]][2])
    {
        minIndex = rc;
    }
    if(minIndex != i)
    {
        Swap(&nums[minIndex],&nums[i]);
        Heapfiy(trips,nums,size,minIndex);
    }
}


//插入堆
void HeapPush(int** trips,int* nums, int* size, int i)
{
    nums[(*size)++] = i;
    for (int parent = (*size - 2) / 2; parent >= 0; parent = (parent - 1) / 2)
    {
        Heapfiy(trips,nums,*size,parent);
        if(parent == 0)
        {
            break;
        }
    }
}



//删除
void HeapPop(int** trips, int* nums, int* size)
{
    Swap(&nums[0],&nums[--(*size)]);
    Heapfiy(trips,nums,*size,0);
}

4. 滑动窗口最大值

在这里插入图片描述
这道题给我们一个k大小的窗口，向右边的滑动，并且求出每一个窗口内的最大值。
下面是两种解法，在这道题目中，单调队列的时间更快。

（1）单调队列

第一种办法我们可以维护一个单调队列出来，此队列为递增序列。

  • 利用两个指针来锁定窗口的大小，left 和 right,
  • 如果right - left != k，就说明窗口还没形成,right一直往后走
  • 否则left++。
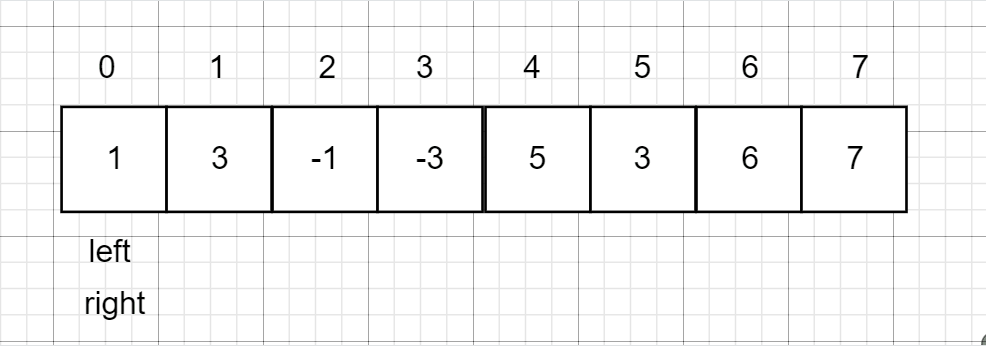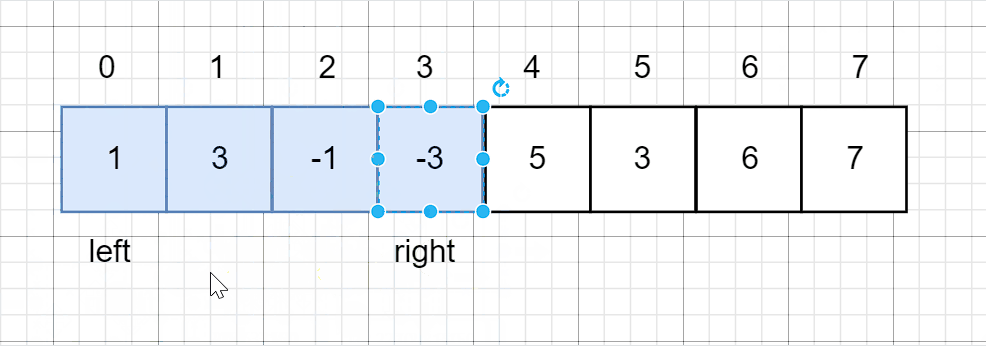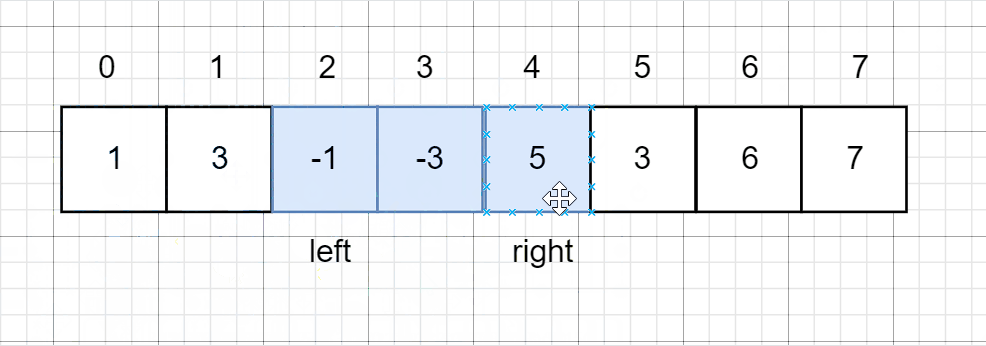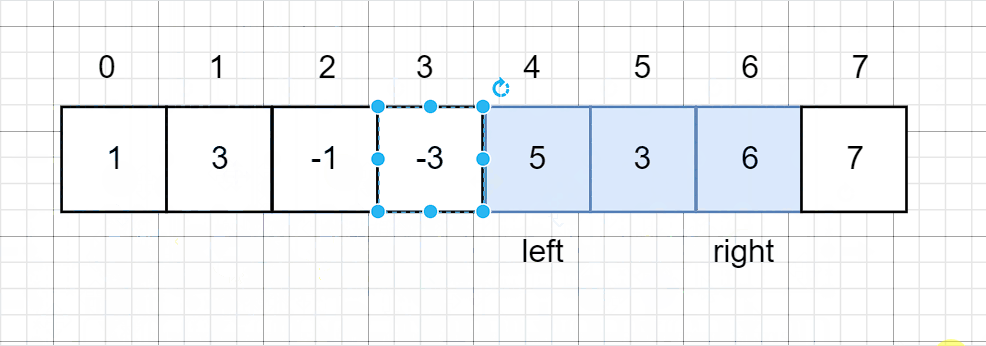
    在这里插入图片描述
    接下来再维护一个单调队列就好了。
  • 队列要保持一个单调递减的队列，这样队首永远都是属于一个最大值。
  • 当我们进行出队列的时候，需要判断当前的left是否是队首的元素，如果是，那么队首也随之而然的消除。
  • 当每次需要更新窗口大小的时候，就是收获结果的时候，我下面是直接在数组中进行修改的。
int* maxSlidingWindow(int* nums, int numsSize, int k, int* returnSize)
{
    int* deQueue = (int*)malloc(sizeof(int) * numsSize);
    int front = 0, rear = 0;
    int left = 0;
    
    for (int i = 0; i < numsSize; i++)
    {
        if(i - left == k)
        {
            //调整窗口大小 && 更新值
            nums[left] = nums[deQueue[front]];
            if(left == deQueue[front])
            {
                front++;
            }
            left++;
        }
        
        //维护单调队列
        while(front != rear && nums[deQueue[rear - 1]] < nums[i])
        {
            rear--;
        }

        //入队列
        deQueue[rear++] = i;
    }
    nums[left++] = nums[deQueue[front]];
    *returnSize = left;
    return nums;
}

（2）优先队列

根据上面的单调队列我们可以发现，只需要对于每个窗口获取最大值就好，所以我们同样也可以用优先队列来存储最大值利用大顶堆。

  • 优先队列中存储的依旧是下标，思路其实和单调队列的思路是一样的。
  • 只是换了一种获取最大值的数据结构而已。
  • 单调队列：获取答案后出队列只需要将等于left对首出队列即可。
  • 优先队列：获取答案后出队列需要将 小于等于left的所有节点出队列
  • 所以优先队列需要一个循环出队列，而单调队列则需要一个if就ok了。

听起来好像优先队列更麻烦，其实不然，因为单调队列还需要维护一下，而优先队列直接插入就好了。

int* maxSlidingWindow(int* nums, int numsSize, int k, int* returnSize)
{
    int* ans = (int*)malloc(sizeof(int) * numsSize);
    int* heap = (int*)malloc(sizeof(int) * numsSize);
    int size = 0, left = 0, pos = 0;
    for (int i = 0; i < numsSize; i++)
    {
        if(i - left == k)
        {
            //修改窗口大小 && 获取ans
            ans[pos++] = nums[heap[0]];
            //最大的数不在窗口内，出队列
            while(size != 0 && heap[0] <= left)
            {
                HeapPop(nums,heap,&size);
            }
            left++;
        }
        //入队列
        HeapPush(nums,heap,&size,i);
    }


    ans[pos++] = nums[heap[0]];
    *returnSize = pos;
    return ans;
}

而对于堆函数的实现，和上一题拼车一样，存储的都是下标，修改修改就能用了。

//heap 中存放下标
void Heapfiy(int* nums, int* heap, int size, int i)
{
    int maxIndex = i, lc = 2 * i + 1, rc = 2 * i + 2;
    if (lc < size && nums[heap[lc]] > nums[heap[maxIndex]])
    {
        maxIndex = lc;
    }
    if (rc < size && nums[heap[rc]] > nums[heap[maxIndex]])
    {
        maxIndex = rc;
    }
    if(maxIndex != i)
    {
        Swap(&heap[i], &heap[maxIndex]);
        Heapfiy(nums,heap,size,maxIndex);
    }
}

//
void HeapPush(int* nums, int* heap, int* size, int i)
{
    heap[(*size)++] = i;
    for (int parent = (*size - 2) / 2; parent >= 0; parent = (parent - 1) / 2)
    {
        Heapfiy(nums,heap,*size,parent);
        if(parent == 0)
        {
            break;
        }
    }
}

void HeapPop(int* nums,int* heap, int* size)
{
    Swap(&heap[0],&heap[--(*size)]);
    Heapfiy(nums,heap,*size,0);
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1457612.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

CoWoS封装产能短缺挑战AI芯片市场需求

CoWoS封装产能短缺挑战AI芯片市场需求

随着人工智能、云计算、大数据分析和移动计算等技术的蓬勃发展&#xff0c;现代社会对计算能力的需求日益高涨。然而&#xff0c;在先进制程突破3纳米后&#xff0c;晶圆尺寸遭遇缩放极限&#xff0c;制造成本也随之上升。因此&#xff0c;除了继续研发先进制程外&#xff0c;半…
阅读更多...
网络防火墙综合实验

网络防火墙综合实验

备注&#xff1a;电信网段15.1.1.0 移动网段14.1.1.0 办公区 11.1.1.0 生产区 10.1.1.0 服务区 13.1.1.0 公网 1.1.1.1 和 2.2.2.2 需求&#xff1a; 1、办公区设备可以通过电信链路和移动链路上网&#xff08;多对多nat&#xff0c;并且需要保留一个公网ip&#xff09; 2、…
阅读更多...
C#，入门教程(05)——Visual Studio 2022源程序（源代码）自动排版的功能动画图示

C#，入门教程(05)——Visual Studio 2022源程序（源代码）自动排版的功能动画图示

上一篇&#xff1a; C#&#xff0c;入门教程(04)——Visual Studio 2022 数据编程实例&#xff1a;随机数与组合https://blog.csdn.net/beijinghorn/article/details/123533838 新来的徒弟们交上来的C#代码&#xff0c;可读性往往很差。 今天一问才知道&#xff0c;他们居然不…
阅读更多...
使用go-llama.cpp 运行 yi-01-6b大模型，使用本地CPU运行，速度挺快的

使用go-llama.cpp 运行 yi-01-6b大模型，使用本地CPU运行，速度挺快的

1&#xff0c;视频地址 2&#xff0c;关于llama.cpp 项目 https://github.com/ggerganov/llama.cpp LaMA.cpp 项目是开发者 Georgi Gerganov 基于 Meta 释出的 LLaMA 模型&#xff08;简易 Python 代码示例&#xff09;手撸的纯 C/C 版本&#xff0c;用于模型推理。所谓推理…
阅读更多...
CMake无Name和Value部分界面

CMake无Name和Value部分界面

鼠标会变成以下 拉开后就 出现想要的部分
阅读更多...
SpaceX 发射军用卫星，用于跟踪高超音速导弹

SpaceX 发射军用卫星，用于跟踪高超音速导弹

上周三&#xff0c;导弹防御局的两颗原型卫星和美国太空军的四颗导弹跟踪卫星搭乘 SpaceX 猎鹰 9 号火箭从佛罗里达州太空海岸进入轨道。 这些卫星是新一代航天器的一部分&#xff0c;旨在跟踪中国或俄罗斯发射的高超音速导弹&#xff0c;以及可能来自正在开发自己的高超音速武…
阅读更多...
蓝桥杯：C++贪心算法、字符串函数、朴素模式匹配算法、KMP算法

蓝桥杯：C++贪心算法、字符串函数、朴素模式匹配算法、KMP算法

贪心算法 贪心(Greedy)算法的原理很容易理解&#xff1a;把整个问题分解成多个步骤&#xff0c;在每个步骤都选取当前步骤的最优方案&#xff0c;直到所有步骤结束&#xff1b;每个步骤都不考虑对后续步骤的影响&#xff0c;在后续步骤中也不再回头改变前面的选择。 贪心算法…
阅读更多...
折叠式隐形纱窗原理

折叠式隐形纱窗原理

如果出现上轨与下轨不同步&#xff0c;可分析是否是某些绳子被拉长导致的。 以上图现象为例&#xff0c;可调整折叠纱窗一侧上部分的4跟组织线长度。从而解决上轨与下轨拉动不同步的问题。
阅读更多...
【天衍系列 01】深入理解Flink的 FileSource 组件：实现大规模数据文件处理

【天衍系列 01】深入理解Flink的 FileSource 组件：实现大规模数据文件处理

文章目录 01 基本概念02 工作原理03 数据流实现04 项目实战4.1 项目结构4.2 maven依赖4.3 StreamFormat读取文件数据4.4 BulkFormat读取文件数据4.5 使用小结 05 数据源比较06 总结 01 基本概念 Apache Flink 是一个流式处理框架&#xff0c;被广泛应用于大数据领域的实时数据…
阅读更多...
报表开发工具DevExpress .NET Reporting v23.2亮点 - 支持智能标签

报表开发工具DevExpress .NET Reporting v23.2亮点 - 支持智能标签

DevExpress Reporting是.NET Framework下功能完善的报表平台&#xff0c;它附带了易于使用的Visual Studio报表设计器和丰富的报表控件集&#xff0c;包括数据透视表、图表&#xff0c;因此您可以构建无与伦比、信息清晰的报表。 DevExpress Reporting控件日前正式发布了v23.2…
阅读更多...
STM32学习·HAL库·STM32CubeMX系列学习（安装和使用）

STM32学习·HAL库·STM32CubeMX系列学习（安装和使用）

目录 ​编辑 1. STM32CubeMX简介 2. STM32CubeMX安装 2.1 STM32CubeMX软件获取 2.1.1 获取Java软件 2.1.2 STM32CubeMX软件获取 2.2 搭建Java运行环境 2.3 安装STM32CubeMX软件 2.4 下载和关联STM32cube固件包 1. STM32CubeMX简介 STM32CubeMX 是 ST 微电子公…
阅读更多...
Go 是否有三元运算符？Rust 和 Python 是怎么做的？

Go 是否有三元运算符？Rust 和 Python 是怎么做的？

嗨&#xff0c;大家好&#xff01;本文是系列文章 Go 技巧第十四篇&#xff0c;系列文章查看&#xff1a;Go 语言技巧。 今天来聊聊在 Go 语言中是否支持三元运算符。这个问题很简单&#xff0c;没有。 首先&#xff0c;什么是三元运算符&#xff1f; 在其他一些编程语言中&a…
阅读更多...
The Sandbox NFT 概览与数据分析

The Sandbox NFT 概览与数据分析

作者&#xff1a;stellafootprint.network 编译&#xff1a;cicifootprint.network 数据源&#xff1a;The Sandbox NFT Collection Dashboard Sandbox NFT 系列包括独特的体素资产和 LAND 地块&#xff0c;使所有者能够在 The Sandbox 元宇宙中构建、玩虚拟体验并从中获…
阅读更多...
【VSCode】设置 一键生成vue模板 的快捷入口

【VSCode】设置 一键生成vue模板 的快捷入口

问题 每次写一个组件的时候&#xff0c;都需要去手敲默认结构或者是复制粘贴&#xff0c;十分的麻烦&#xff01; 解决办法 文件 > 首选项 > 用户代码片段 > vue.json 配置vue模板 其中prefix是用来触发代码段的内容&#xff0c;即模版的快捷入口&#xff1b;body里…
阅读更多...
红帽认证——步入优质职场的第一步

红帽认证——步入优质职场的第一步

在当今数字化时代&#xff0c;掌握先进的技术和技能是开启成功职业生涯的关键。红帽认证课程将为你提供这样的机会&#xff0c;帮助你成为一名具备实际操作能力的专业人士。Redhat&#xff0c;红帽公司是全球知名的开源技术厂家&#xff0c;领先的开源解决方案供应商。Linux有很…
阅读更多...
Python Flask高级编程之RESTFul API前后端分离（学习笔记）

Python Flask高级编程之RESTFul API前后端分离（学习笔记）

Flask-RESTful是一个强大的Python库&#xff0c;用于构建RESTful APIs。它建立在Flask框架之上&#xff0c;提供了一套简单易用的工具&#xff0c;可以帮助你快速地创建API接口。Flask-RESTful遵循REST原则&#xff0c;支持常见的HTTP请求方法&#xff0c;如GET、POST、PUT和DE…
阅读更多...
Datawhale零基础入门金融风控Task1 赛题理解

Datawhale零基础入门金融风控Task1 赛题理解

Task1 赛题理解 Tip:本次新人赛是Datawhale与天池联合发起的0基础入门系列赛事第四场 —— 零基础入门金融风控之贷款违约预测挑战赛。 赛题以金融风控中的个人信贷为背景&#xff0c;要求选手根据贷款申请人的数据信息预测其是否有违约的可能&#xff0c;以此判断是否通过此项…
阅读更多...
Office2019安装冲突解决方法 ErrorCode 30182-392

Office2019安装冲突解决方法 ErrorCode 30182-392

问题描述 挂载安装Office 2019安装镜像后直接安装会出现如下的错误&#xff1a; 问题原因在于Office 365与Offfice2019版本号相同&#xff08;均为16.0&#xff09;官方页面-各Office版本号 解决办法 解决方法就是利用官方部署工具进行安装&#xff0c;绕过版本冲突问题 …
阅读更多...
ansible剧本中的角色

ansible剧本中的角色

1 roles角色 1.1 roles角色的作用&#xff1f; 可以把playbook剧本里的各个play看作为一个角色&#xff0c;将各个角色打的tasks任务、vars变量、template模版和copy、script模块使用的相关文件等内容放置在指定角色的目录里统一管理&#xff0c;在需要的时候可在playbook中使…
阅读更多...
从可靠性的角度理解 tcp

从可靠性的角度理解 tcp

可靠性是 tcp 最大的特点。常见的用户层协议&#xff0c;比如 http, ftp, ssh, telnet 均是使用的 tcp 协议。可靠性&#xff0c;即从用户的角度来看是可靠的&#xff0c;只要用户调用系统调用返回成功之后&#xff0c;tcp 协议栈保证将报文发送到对端。引起不可靠的表现主要有…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023