Every day a Leetcode

题目来源：3011. 判断一个数组是否可以变为有序

解法1：分组循环 + 排序

适用场景：按照题目要求，数组会被分割成若干组，每一组的判断/处理逻辑是相同的。

核心思想：

1. 外层循环负责遍历组之前的准备工作（记录开始位置），和遍历组之后的工作（排序）。
2. 内层循环负责遍历组，找出这一组最远在哪结束。

这个写法的好处是，各个逻辑块分工明确，也不需要特判最后一组（易错点）。

用分组循环找到一个组， 对这个组排序，最后判断整个数组是否有序。

代码：

/*
 * @lc app=leetcode.cn id=3011 lang=cpp
 *
 * [3011] 判断一个数组是否可以变为有序
 */

// @lc code=start
class Solution
{
public:
    bool canSortArray(vector<int> &nums)
    {
        int n = nums.size();
        int i = 0;

        // 分组循环
        while (i < n) // 外层循环
        {
            int ones = countOne(nums[i]);
            int start = i;
            // 内层循环
            while (i < n && countOne(nums[i]) == ones)
                i++;
            // 循环结束后 nums[start,...,i) 是一个区间
            sort(nums.begin() + start, nums.begin() + i);
        }
        return is_sorted(nums.begin(), nums.end());
    }
    // 辅函数 - 计算 x 在二进制下数位为 1 的数目
    int countOne(int x)
    {
        int count = 0;
        while (x)
        {
            count += x % 2;
            x /= 2;
        }
        return count;
    }
};
// @lc code=end

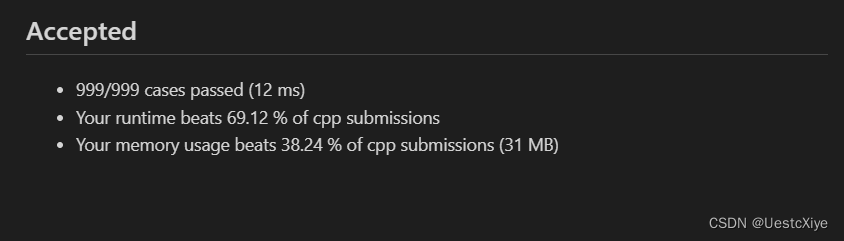
结果：

复杂度分析：

时间复杂度：O(nlogn)，其中 n 是数组 nums 的元素个数。

空间复杂度：O(1)。

解法2：分组循环

也可以记录每一段的最小值和最大值。

对于每一段，如果这一段的每个数，都大于等于上一段的最大值，那么我们就能把数组排成递增的，否则不行。

代码：

class Solution {
public:
    bool canSortArray(vector<int> &nums) {
        int n = nums.size();
        int i = 0, pre_max = 0;
        while (i < n) {
            int mx = nums[i];
            int ones = __builtin_popcount(mx);
            while (i < n && __builtin_popcount(nums[i]) == ones) {
                if (nums[i] < pre_max) {
                    return false;
                }
                mx = max(mx, nums[i++]);
            }
            pre_max = mx;
        }
        return true;
    }
};

复杂度分析：

时间复杂度：O(n)，其中 n 是数组 nums 的元素个数。

空间复杂度：O(1)。