介绍

对于网图来说，最短路径是指两顶点之间经过的边上权值之和最少的路径，其路径上第一个点记为源点，最后一个为终点。

计算最短路径有两个经典算法，即迪杰斯特拉（Dijkstra）算法与弗洛伊德（Floyd）算法。

Dijkstra算法

这个算法是从一个给定的顶点出发，不断计算更新此顶点到目标顶点的最短路径

假如有这样一张网图

如果我们要求顶点0到顶点1的最短距离，那无疑是1。由于1还与2，3相连，所以我们也可以求出0->1->2的距离为1+2=3，0->1->3距离为1+4=5；

但如果求从顶点0到顶点2的最短距离，由于边上都有权值，5是大于3的，所以0到2的最短距离是3；

同时，因为2与3,4相连，我们可以求得由此路径的0->1->2->3=3+1=4,0->1->2->4的距离为4+4=7；而这条路径上0到3的距离要小于上述0->1->3那条，则目前0到3的最短距离更新为4

... ...以此类推，不断基于已经求出的中途的最短距离，来更新到目标顶点的最短路径，这就是这个算法的核心思想

具体代码实现

	typedef struct{
	int vex[max];//顶点数组
	int arc[max][max];//带权边长
	int numN,numE;//顶点数及边数
}Mgraph;//用邻接矩阵存储整张图
int p[max];//储存最短路径下标数组
int d[max];//储存到各点的最短路径权值和
void SPDijkstra(Mgraph g,int v0){//传入图与起始顶点
	int m;
	int final[max];//记录从v0到i顶点的最短路径
	for (int i=0;i<g.numN;i++){
		final[i]=0;//初始化未未知最短路径的状态
		d[i]=g.arc[v0][i];//将所有与v0有连线的加上权值
		p[i]=-1;//初始化路径数组为-1
	}
	d[v0]=0;//v0至v0距离为0
	final[v0]=1;//标记v0至v0不需要求路径
	int k;
	for (int i=1;i<g.numN;i++){//从v1开始找起
		m=INT_MAX;
		for (int j=0;j<g.numN;j++){
			if (!final[j]&&d[j]<m){
				m=d[j];
				k=j;//记录距v0最短的带权路径顶点
			}
		}
		final[k]=1;//标记此顶点
     //开始更新最短距离
		for (int j=0;j<g.numN;j++){
			if (!final[j]&&m+g.arc[k][j]<d[j]){
				d[j]=m+g.arc[k][j];//更新v0到j的最短路径
				p[j]=k;//v0到j顶点的最短路径前驱是k
			}
		}
	}
}

Floyd算法

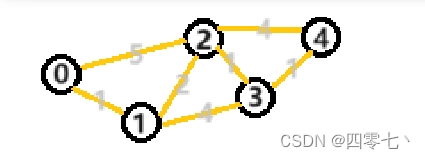
还是以此图为例

弗洛伊德算法常用于求取所有顶点至所有顶点的最短路径，它利用动态规划的方法，将顶点至顶点间的最短路径记录在一个二维数组中

在带权的邻接矩阵中，arc[i][j]记录的为i j之间的距离，如例图中arc[0][2]=5

但如果找一个与两个顶点都相连的中间节点，如1，计算得出arc[0][1]+arc[1][2]=1+2=3，这个值是小于5的，这条路径的距离就可以更新到矩阵中代替5的位置

利用这种算法进行重复迭代，对于每一对顶点i,j，遍历所有的中间节点k，检查是否存在一条路径比当前更短，如果是则更新矩阵中的最短距离。这样就可以的出两个个顶点之间的最短路径与最短距离。

代码实现如下

int p[max][max];//p数组记录路径，方便后续输出最短路径
int d[max][max];//记录最短距离
void SPFloyd(Mgraph g){
	for (int i=0;i<g.numN;i++){
		for (int j=0;j<g.numN;j++){
			d[i][j]=g.arc[i][j];//初始化为邻接矩阵
			p[i][j]=j;//初始化路径数组
		}
	}
	for(int k=0;k<g.numN;k++){
		for (int i=0;i<g.numN;i++){
			for (int j=0;j<g.numN;j++){
				if(d[i][j]>d[i][k]+d[k][j]){
					d[i][j]=d[i][k]+d[k][j];//更新最短距离
					p[i][j]=p[i][k];//更新路径，即要到j的最短路径中，j之前一个顶点为k
				}
			}
		}
	}
}