欢迎关注更多精彩
关注我，学习常用算法与数据结构，一题多解，降维打击。

本期话题：线性规划单纯形法原理及实现

标准化及单纯形方法

相关学习资料
https://www.bilibili.com/video/BV168411j7XL/?spm_id_from=333.788&vd_source=fb27f95f25902a2cc94d4d8e49f5f777

标准化形式

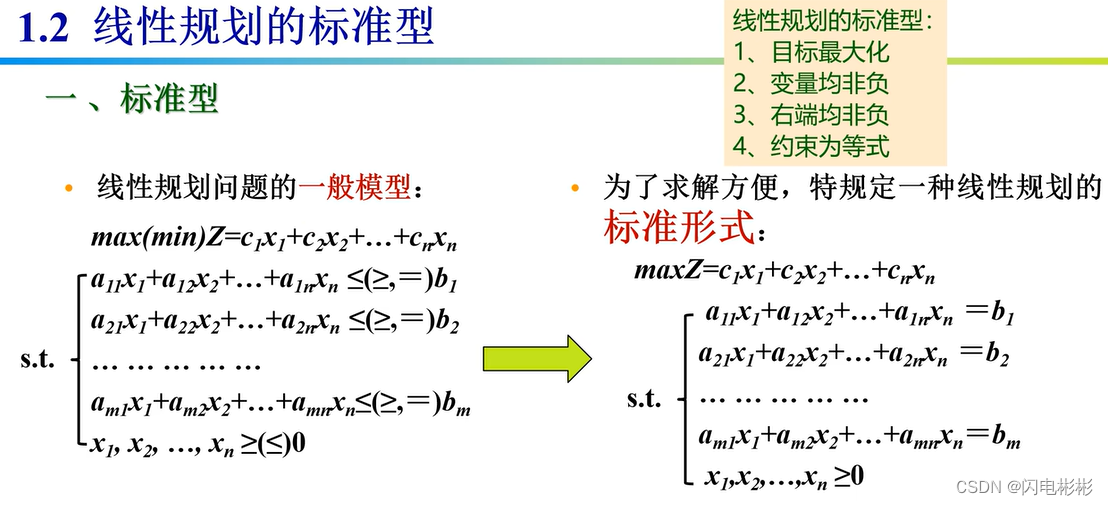
标准化数学表示如下：

$\begin{array}{c}maxf(x)=c^{T}x\\ s.t.Ax=b(b\ge 0)\\ x\ge 0\end{array}$

标准化方法

单纯形法

https://www.bilibili.com/video/BV1xr4y1V7Ae/?spm_id_from=333.788&vd_source=fb27f95f25902a2cc94d4d8e49f5f777

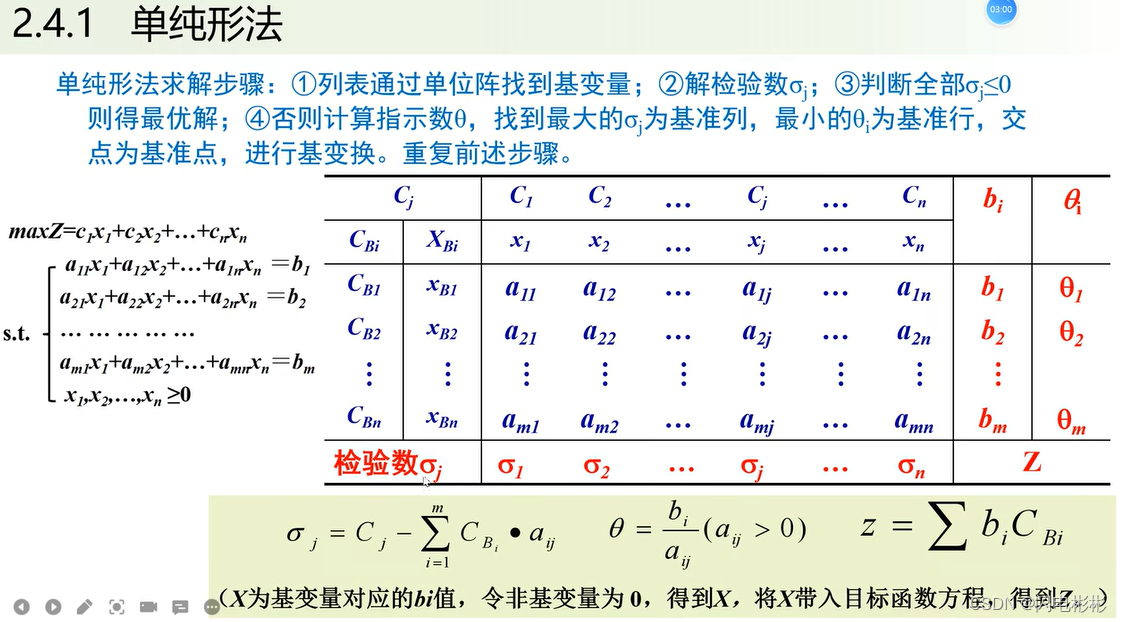
例题演示

整个过程本质上是一个矩阵行变换过程

练习1 有解

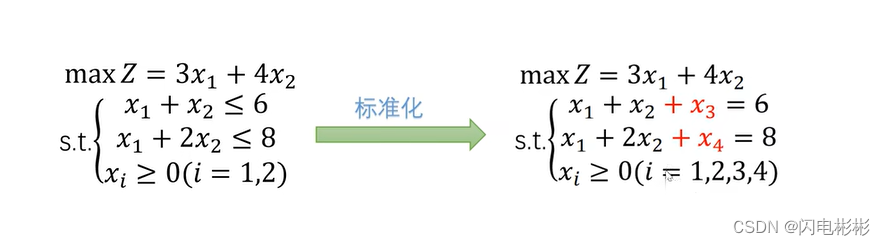
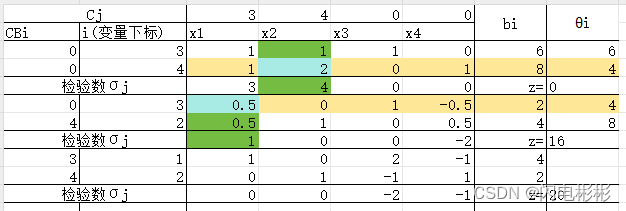
大M法

大M法是在标准化以后无法找到一组单位向量作为基变量，不能直接进行单纯形法求解。
需要添加人工变量构造单位向量，同时要对函数添加惩罚项。

$\begin{array}{l}maxZ=3x_1+4x_2\\ \{\begin{array}{l}{x}_1+x_2\le 6\\ x_1+2x_2\ge 8\\ x_i\ge 0(i=1,2)\end{array}\end{array}$

对上式进行标准化

$\begin{array}{l}maxZ=3x_1+4x_2\\ \{\begin{array}{l}{x}_1+x_2+x_3=6\\ x_1+2x_2-x_4=8\\ x_i\ge 0(i=1,2,3,4)\end{array}\end{array}$

上式中最后2个变量组成的矩阵是

$\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]$

不是单位矩阵，已经有1列是单位向量，需要再加1列人工变量。
M是一个很大的正数。

$\begin{array}{l}maxZ=3x_1+4x_2-x_{5}M\\ \{\begin{array}{l}{x}_1+x_2+x_3=6\\ x_1+2x_2-x_4+x_5=8\\ x_i\ge 0(i=1,2,3,4,5)\end{array}\end{array}$

添加人加变量后，就可以按照单纯形法来求解了。

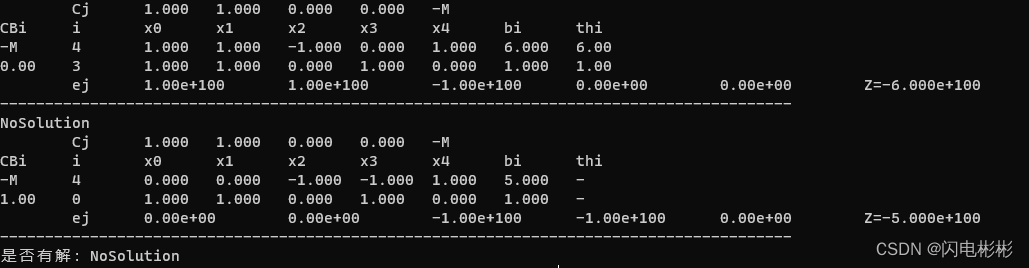
解的情况

• 唯一解：当所有解检验数σ都小于0时。
• 多个解：当所有解检验数σ都小于0且至少有1个检验数=0时。
• 无上界解：不管取到多大的值，总有更大的，也是无解的一种情况。条件是存在1个检验数大于0且列向量系数都小于0的列。
• 无解：当所有解检验数σ都小于等于0且存在人工变量为基变量。

算法实现

算法步骤

• 对问题进行标准化
• 添加松驰变量
• 检查是否有单位矩阵，若没有则添加相应的人工变量
• 按照单纯形法进行迭代

核心代码设计

class LPS
		{
		public:
			/*
			* 初始化
			* 设定变量个数，目标函数系数，优化类型
			*/
			void InitProb(int n, std::vector<double> &c, OptimizationType ot);
			/*
			* 添加条件
			* 向量x前面是x系数, b代表右边常数，ct代表符号
			*/
			void AddCondition(std::vector<double> &x, double b, CmpType ct);

			/*
			* 求解规划
			*/
			Result solve();

		private:
			OptimizationType OT;
			int varNums; 
			std::vector<double> originCeff;
			std::vector<std::vector<double>> conditionsCeff;
			std::vector<double> conditionsB;
			std::vector<CmpType> conditionsCmpType;


		private:
			// 运算过程变量
			std::vector<double> ceff; // 标准化后的系数
			std::vector<std::unordered_map<int , double>> equaltations;// 等式
			std::vector<VarType> varType;
			int sysRelaxNumMark;// 松驰变量+原始变量个数
			Result res;
			Eigen::Matrix<double, -1, -1> determinant; // 行列式
			std::vector<int> baseVarInd; // 基变量编号

			/*
			* 标准化
			*/
			void normalize();

			/*
			* 添加松驰变量，构造等式
			*/
			void addRelaxVar();

			/*
			* 添加人工变量, 获得初始基
			*/
			void addManualVar();

			/*
			* 迭代
			*/
			void iteration();

			/*
			* 汇总结果
			*/
			void genResult();


			/*
			* 中间过程
			*/
			void printFram(const std::vector<double>& sigma, const std::vector<double>& theta);
		};

代码实现

https://gitcode.com/chenbb1989/3DAlgorithm/blob/master/commonFunc/BasicTools/Math/Simplex.cpp
#pragma once

#include "../include/Math/Simplex.h"
#include <iostream>

#define SIMPLEXDEBUG

using namespace BasicTools;
using namespace Simplex;

int BasicTools::Simplex::CmpDouble(double a)
{
	if (abs(a) < EPS)return 0;
	if (a > 0)return 1;
	return -1;
}

void LPS::InitProb(int n, std::vector<double> &c, OptimizationType ot)
{
	assert(ceff.size() == n);
	std::cout << "InitProb" << std::endl;
	varNums = n;
	OT = ot;
	originCeff = c;
	conditionsCeff.clear();
	conditionsB.clear();
	conditionsCmpType.clear();
}

void LPS::AddCondition(std::vector<double> &x, double b, CmpType ct)
{
	assert(x.size() == varNums);
	conditionsCeff.push_back(x);
	conditionsB.push_back(b);
	conditionsCmpType.push_back(ct);
}

Result LPS::solve()
{
	normalize();
	addRelaxVar();
	addManualVar();
	iteration();
	genResult();
	return res;
}

LPS::~LPS()
{
}

void BasicTools::Simplex::LPS::normalize()
{
	ceff = originCeff;
	// 优化类型检查
	if (OT == MIN)for (auto& c : ceff)c *= -1;
	varType.assign(varNums, Sys);

	// 对条件检查bi是否都大于0
	for (int i = 0; i < conditionsCeff.size(); ++i) {
		if (conditionsB[i] < 0) {
			for (auto& c : conditionsCeff[i])c *= -1;
			conditionsB[i] *= -1;
			if (conditionsCmpType[i] != EQ)conditionsCmpType[i] =CmpType(int(conditionsCmpType[i]) ^1);
		}
	}

}

void BasicTools::Simplex::LPS::addRelaxVar()
{
	// 利用map存储等式
	equaltations.resize(conditionsCmpType.size());
	for (int i = 0; i < equaltations.size(); ++i) 
		for (int j = 0; j < conditionsCeff[i].size(); ++j) equaltations[i][j] = conditionsCeff[i][j];

	for (int i = 0; i < conditionsCmpType.size();++i) {
		auto t = conditionsCmpType[i];
		if (t != EQ) {
			varType.push_back(Relax);
			ceff.push_back(0);
		}

		if (t == GE) {
			equaltations[i][ceff.size() - 1] = -1;
		}
		else if(t==LE)
		{
			equaltations[i][ceff.size() - 1] = 1;
		}
	}
	sysRelaxNumMark = varType.size();
}

double getCeff(std::unordered_map<int, double>& m, int j) {
	if (m.count(j) == 0)return 0;
	return m[j];
}

void BasicTools::Simplex::LPS::addManualVar()
{
	baseVarInd.resize(equaltations.size());
	for (int i = 0; i < equaltations.size(); ++i) {
		// 先从松驰变量中找基变量
		baseVarInd[i] = -1;
		for (int j = 0; j < sysRelaxNumMark; ++j) {
			// 判断是否为单位向量且当前行为1
			if (CmpDouble(getCeff(equaltations[i],j)-1))continue;

			// 判断其余行为0
			bool find = true ;
			for (int k = 0; k < equaltations.size() && find; ++k) {
				if (k == i)continue;
				if (CmpDouble(getCeff(equaltations[k], j))) find = false;
			}

			if (find) {
				baseVarInd[i] = j;
				break;
			}

		}

		// 没找到，添加人工变量，优化函数系数中加入大-M
		if (baseVarInd[i] == -1) {
			baseVarInd[i] = varType.size();
			equaltations[i][varType.size()] = 1;
			ceff.push_back(-BIGM);
			varType.push_back(Manual);
		}
	}
}

void BasicTools::Simplex::LPS::iteration()
{	
	std::vector<double> baseCeff(baseVarInd.size()); // CBi
	std::vector<bool> isBaseVar(varType.size(), false);
	for (int i = 0; i < baseVarInd.size(); ++i) {
		baseCeff[i] = ceff[baseVarInd[i]];
		isBaseVar[baseVarInd[i]] = true;
	}
	int n = baseVarInd.size(), m = ceff.size()+1;
	// 构造行列式
	determinant.resize(baseVarInd.size(), m);
	for (int i = 0; i < n; ++i) {
		for (int j = 0; j < m - 1; ++j)
			determinant(i, j) = getCeff(equaltations[i], j);
		determinant(i, m - 1) = conditionsB[i];
	}	

	// 单纯形迭代
	while (1) {
		int inBase = -1, outBase=-1;
		double sigma = 0, theta=0;
		std::vector<double> sigmas(ceff.size(), 0), thetas(n, BIGM);

		// 计算sigma确定进基
		for (int i = 0; i < varType.size(); ++i) {
			// 基变量不用算肯定是0
			if (isBaseVar[i])continue;

			double t = ceff[i];
			bool unbound = true;
			for (int j = 0; j < n; ++j) {
				t -= baseCeff[j] * determinant(j, i);
				if (unbound && determinant(j, i) > 0)unbound = false;
			}
			sigmas[i] = t;
			if (unbound && t > 0) {
				std::cout << "NoUpBound" << std::endl;
				res.rt = NoUpBound;
#ifdef SIMPLEXDEBUG
				printFram(sigmas, thetas);
#endif
				return;
			}
			if (sigma < t) {
				inBase = i;
				sigma = t;
			}
			if (CmpDouble(t) == 0 && inBase == -1) {
				inBase = -2;
			}
		}

		// 迭代结束，先判断是否无解，查看基变量是否有人工变量		
		for (int i = 0; i < baseVarInd.size() && inBase<0;++i) {
			if (varType[baseVarInd[i]] == Manual) {
				res.rt = NoSolution;
				std::cout << "NoSolution" << std::endl;
#ifdef SIMPLEXDEBUG
				printFram(sigmas, thetas);
#endif
				return;
			}
		}

		// 有解, 结束
		if (inBase == -1) {
			res.rt = OnlyOne;
#ifdef SIMPLEXDEBUG
			printFram(sigmas, thetas);
#endif
			return;
		}
		if(inBase==-2)
		{
			res.rt = More;
#ifdef SIMPLEXDEBUG
			printFram(sigmas, thetas);
#endif
			return;
		}

		// 还没结束，继续找退基
		for (int i = 0; i < equaltations.size(); ++i) {
			if(CmpDouble(determinant(i, inBase))<=0)continue;
			auto t = determinant(i, m - 1) / determinant(i, inBase);
			thetas[i] = t;
			if (outBase == -1 || t < theta) {
				theta = t;
				outBase = i;
			}
		}

#ifdef SIMPLEXDEBUG
		printFram(sigmas, thetas);
#endif
		//换基
		isBaseVar[baseVarInd[outBase]] = false;
		baseVarInd[outBase] = inBase;
		baseCeff[outBase] = ceff[inBase];
		isBaseVar[inBase] = true;

		// 变换行列式
		double v = determinant(outBase, inBase);
		for (int j = 0; j < m; ++j)determinant(outBase, j) /= v;

		for (int i = 0; i < n; ++i) {
			if (i == outBase)continue;
			v= determinant(i, inBase);
			for (int j = 0; j < m; ++j)determinant(i, j) -= determinant(outBase,j)*v;
		}
	}
}

void BasicTools::Simplex::LPS::genResult()
{
	if (res.rt == NoUpBound || res.rt == NoSolution)return;
	res.Z = 0;
	res.x.assign(varNums, 0);
	for (int i = 0; i < baseVarInd.size(); ++i) {
		res.Z += ceff[baseVarInd[i]] * determinant(i, varType.size());
		res.x[baseVarInd[i]] = determinant(i, varType.size());
	}
	if (OT == MIN)res.Z *= -1;	

#ifdef SIMPLEXDEBUG
	printf("求解类型：%s\n", OT == MIN ? "MIN" : "MAX");
	/*printf("是否有解：");
	switch (res.rt)
	{
	case NoUpBound:
		puts("NoUpBound");
		return;
	case NoSolution:
		puts("NoSolution");
		return;
	case More:
		puts("More");
		break;
	case OnlyOne:
		puts("OnlyOne");
		break;
	default:
		break;
	}

	printf("Z=%.3f\n", res.Z);
	printf("X取值\n");

	for (int i = 0; i < res.x.size(); ++i) 
		printf("x%d: %.3f\n", i, res.x[i]);*/
#endif
}

void BasicTools::Simplex::LPS::printFram(const std::vector<double>& sigma, const std::vector<double>& theta)
{
	double z = 0;
	//	第一行
	printf("\tCj\t");
	for (int i = 0; i < ceff.size(); ++i) {
		if (CmpDouble(BIGM + ceff[i]) == 0) {
			printf("-M\t");
		}
		else {
			printf("%.3f\t", ceff[i]);
		}
	}
	puts("");
	//	第二行
	printf("CBi\ti\t");
	for (int i = 0; i < ceff.size(); ++i) {
		printf("x%d\t", i);
	}
	printf("bi\tthi\t");
	puts("");
	// 打印变量
	int m = ceff.size() + 1;
	for (int i = 0; i < baseVarInd.size(); ++i) {
		if (CmpDouble(BIGM + ceff[baseVarInd[i]])==0) printf("-M");
		else printf("%.2f", ceff[baseVarInd[i]]);
		printf("\t%d\t", baseVarInd[i]);

		for (int j = 0; j < m; ++j) {
			printf("%.3f\t", determinant(i, j));
		}
		z += determinant(i, m - 1)* ceff[baseVarInd[i]];
		if (CmpDouble(BIGM - theta[i]))printf("%.2f\t", theta[i]);
		else printf("-\t");
		puts("");
	}

	// 检验数
	printf("\tej\t");
	for (int i = 0; i < ceff.size(); ++i) {
		printf("%.2e\t", sigma[i]);
		//std::cout << std::scientific << std::precision(2) << sigma[i];
	}

	printf("Z=%.3e\t", z);
	puts("");
	puts("----------------------------------------------------------------------------------------");

}

测试文件格式

0（表示目标函数是max）；1（表示目标函数是min）  

3 3 约束条件矩阵维数，第一个是变量个数，第二个是约束条件个数

4 5 1   目标函数系数向量

3 2 1 18 0         最后一个数字表示约束条件符号，0表示大于等于

2 1 0 4 1          最后一个数字表示约束条件符号，1表示小于等于

1 2 0 5 2         最后一个数字表示约束条件符号，2表示等于

效果测试

文件路径：https://gitcode.com/chenbb1989/3DAlgorithm/tree/master/Tests/BasicTest/SimplexTest
t1

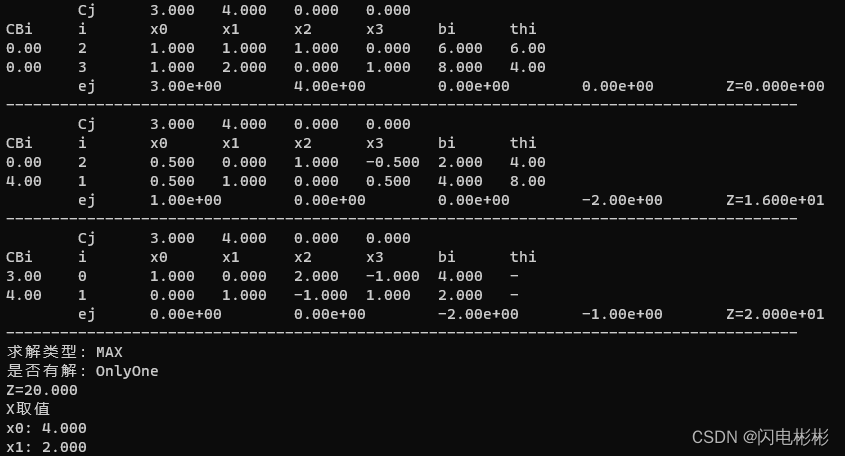
t2

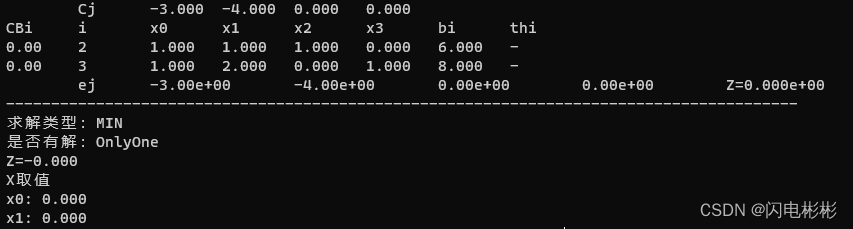
t3

t4

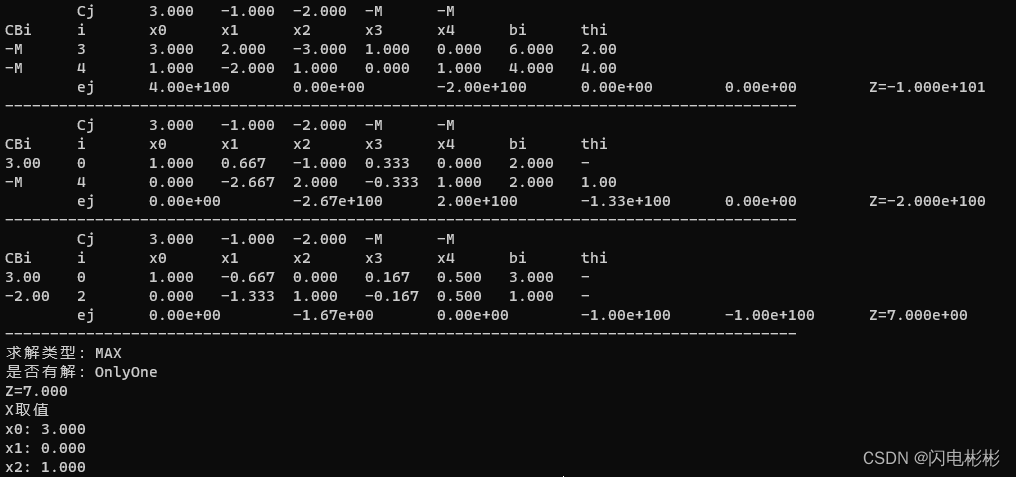
t5

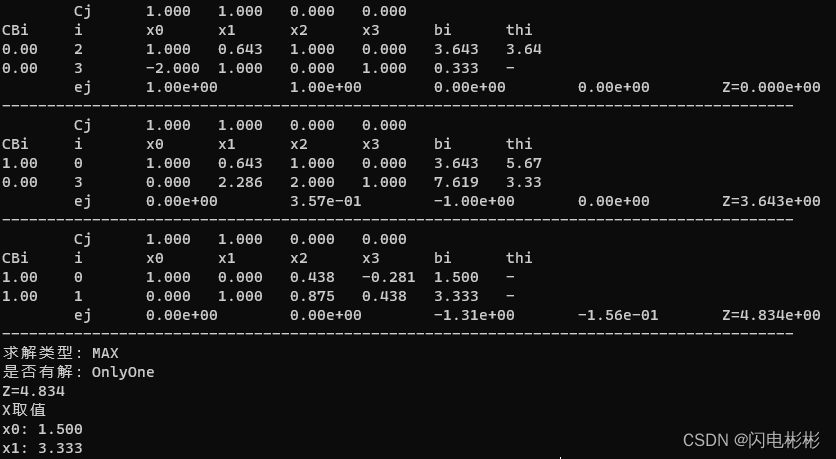
t6

---

本人码农，希望通过自己的分享，让大家更容易学懂计算机知识。创作不易，帮忙点击公众号的链接。