关联规则概述
关联规则(Association Rules)反映一个事物与其他事物之间的相互依存性和关联性。如果两个或者多个事物之间存在一定的关联关系,那么,其中一个事物就能够通过其他事物预测到。

关联规则可以看作是一种IF-THEN关系。假设商品A被客户购买,那么在相同的交易ID下,商品B也被客户挑选的机会就被发现了。
有没有发生过这样的事:你出去买东西,结果却买了比你计划的多得多的东西?这是一种被称为冲动购买的现象,大型零售商利用机器学习和Apriori算法,让我们倾向于购买更多的商品。
购物车分析是大型超市用来揭示商品之间关联的关键技术之一。他们试图找出不同物品和产品之间的关联,这些物品和产品可以一起销售,这有助于正确的产品放置。
买面包的人通常也买黄油。零售店的营销团队应该瞄准那些购买面包和黄油的顾客,向他们提供报价,以便他们购买第三种商品,比如鸡蛋。因此,如果顾客买了面包和黄油,看到鸡蛋有折扣或优惠,他们就会倾向于多花些钱买鸡蛋。这就是购物车分析的意义所在。
基本概念
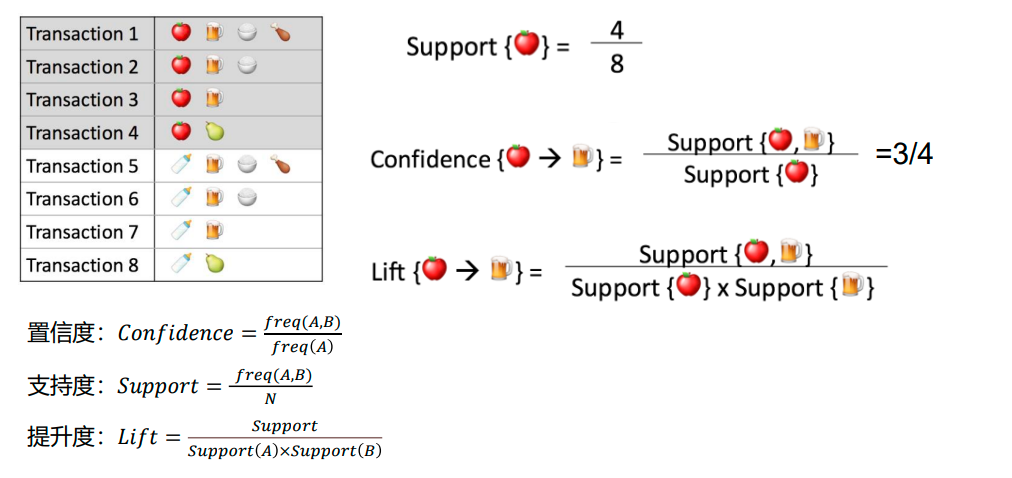
置信度: 表示你购买了A商品后,你还会有多大的概率购买B商品。

支持度: 指某个商品组合出现的次数与总次数之间的比例,支持度越高表示该组合出现的几率越大。

提升度: 提升度代表商品A的出现,对商品B的出现概率提升了多少,即“商品 A 的出现,对商品 B 的出现概率提升的”程度。

实例
Apriori算法
Apriori算法利用频繁项集生成关联规则。它基于频繁项集的子集也必须是频繁项集的概念。
频繁项集是支持值大于阈值(support)的项集。
Apriori算法就是基于一个先验:
如果某个项集是频繁的,那么它的所有子集也是频繁的。
算法流程
输入:数据集合D,支持度阈值𝛼
输出:最大的频繁k项集
- 1)扫描整个数据集,得到所有出现过的数据,作为候选频繁1项集。k=1,频繁0项集为空集。
- 2)挖掘频繁k项集
a) 扫描数据计算候选频繁k项集的支持度
b) 去除候选频繁k项集中支持度低于阈值的数据集,得到频繁k项集。如果得到的频繁k项集为空,则直接返回频繁k-1项集的集合作为算法结果,算法结束。如果得到的频繁k项集只有一项,则直接返回频繁k项集的集合作为算法结果,算法结束。
c) 基于频繁k项集,连接生成候选频繁k+1项集。 - 3) 令k=k+1,转入步骤2。
算法案例
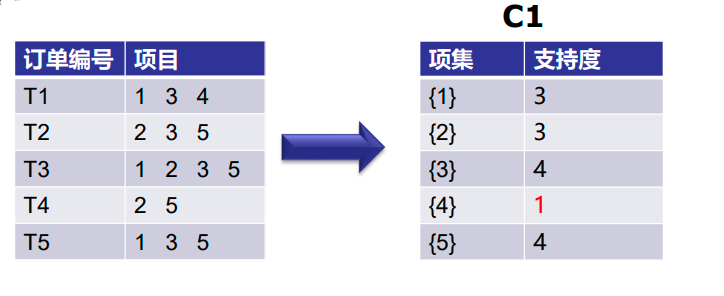
第一次迭代:假设支持度阈值为2,创建大小为1的项集并计算它们的支持度。
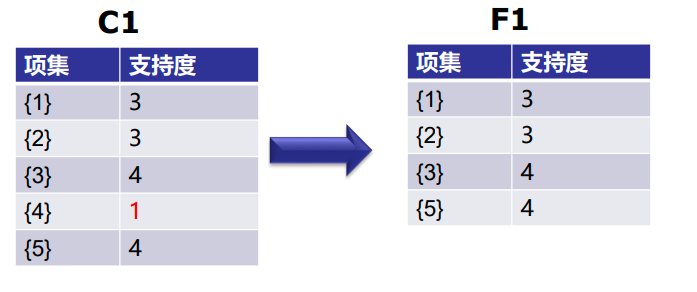
可以看到,第4项的支持度为1,小于最小支持度2。所以我们将在接下来的迭代中丢弃{4}。我们得到最终表F1。
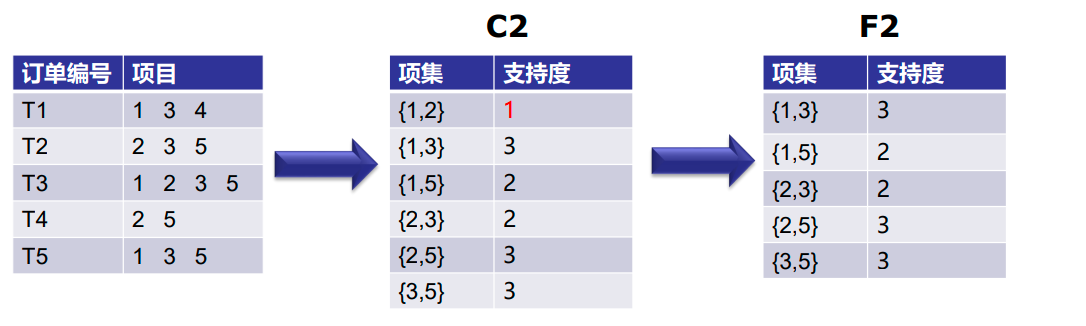
第2次迭代:接下来我们将创建大小为2的项集,并计算它们的支持度。F1中设置的所有项
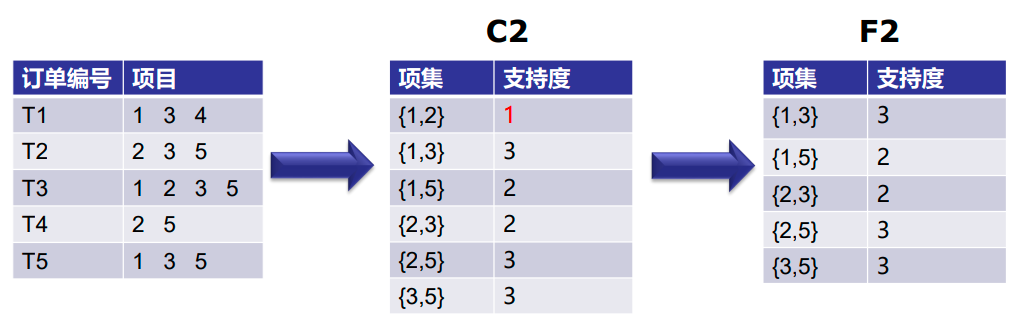
再次消除支持度小于2的项集。在这个例子中{1,2}。
现在,让我们了解什么是剪枝,以及它如何使Apriori成为查找频繁项集的最佳算法之一。
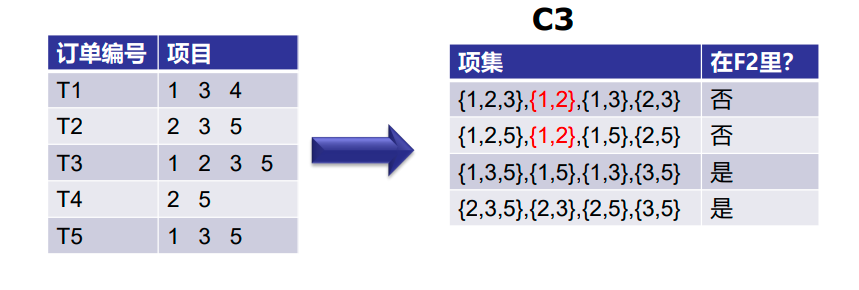
剪枝:我们将C3中的项集划分为子集,并消除支持值小于2的子集。
第三次迭代:我们将丢弃{1,2,3}和{1,2,5},因为它们都包含{1,2}。

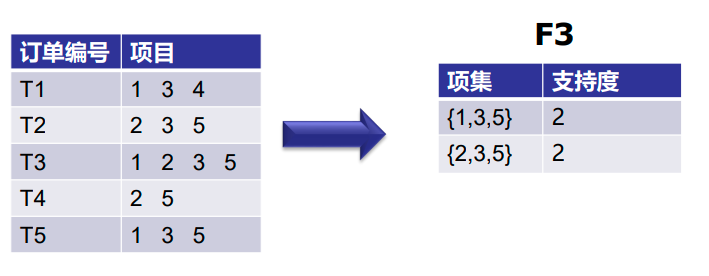
第四次迭代:使用F3的集合,我们将创建C4。
因为这个项集的支持度小于2,所以我们就到此为止,最后一个项集是F3。
注:到目前为止,我们还没有计算出置信度。
使用F3,我们得到以下项集:
对于I={1,3,5},子集是{1,3},{1,5},{3,5},{1},{3},{5}
对于I={2,3,5},子集是{2,3},{2,5},{3,5},{2},{3},{5}
应用规则:我们将创建规则并将它们应用于项集F3。现在假设最小置信值是60%。
对于I的每个子集S,输出规则
• S–>(I-S)(表示S推荐I-S)
• 如果:支持度(l)/支持度(S)>=最小配置值
{1,3,5}
规则1:{1,3}–>({1,3,5}–{1,3})表示1&3–>5
置信度=支持度(1,3,5)/支持度(1,3)=2/3=66.66%>60%
因此选择了规则1
规则2:{1,5}–>({1,3,5}–{1,5})表示1&5–>3
置信度=支持度(1,3,5)/支持度(1,5) =2/2=100%>60%
因此选择了规则2
规则3:{3,5}–>({1,3,5}–{3,5})表示3&5–>1
置信度=支持度(1,3,5)/支持度(3,5)=2/3=66.66%>60%
因此选择规则3
规则4:{1}–>({1,3,5}–{1})表示1–>3&5
置信度=支持度(1,3,5)/支持度(1)=2/3=66.66%>60%
因此选择规则4
规则5:{3}–>({1,3,5}–{3})表示3–>1和5
置信度=支持度(1,3,5)/支持度(3)=2/4=50%<60%
规则5被拒绝
规则6:{5}–>({1,3,5}–{5})表示5–>1和3
置信度=支持度(1,3,5)/支持度(5)=2/4=50%<60%
规则6被拒绝
Apriori算法缺点
计算过程可能产生大量的候选集。因为采用排列组合的方式,把可能的项集都组合出来了;
每次计算都需要重新扫描数据集,来计算每个项集的支持度。
FP-growth( Frequent Pattern Growth )
FP-growth算法思想
FP-growth(频繁模式增长)算法是韩家炜老师在2000年提出的关联分析算法,它采取如下分治策略:将提供频繁项集的数据库压缩到一棵频繁模式树(FP-Tree),但仍保留项集关联信息。
该算法是对Apriori方法的改进。生成一个频繁模式而不需要生成候选模式。
FP-growth算法以树的形式表示数据库,称为频繁模式树或FP-tree。此树结构将保持项集之间的关联。数据库使用一个频繁项进行分段。这个片段被称为“模式片段”。分析了这些碎片模式的项集。因此,该方法相对减少了频繁项集的搜索。
FP-growth算法是基于Apriori原理的,通过将数据集存储在FP(Frequent Pattern)树上发现频繁项集,但不能发现数据之间的关联规则。FP-growth算法只需要对数据库进行两次扫描,而Apriori算法在求每个潜在
的频繁项集时都需要扫描一次数据集,所以说Apriori算法是高效的。
-
其中算法发现频繁项集的过程是:
(1)构建FP树;
(2)从FP树中挖掘频繁项集。 -
FP-Tree ( Frequent Pattern Tree )
FP树(FP-Tree)是由数据库的初始项集组成的树状结构。 FP树的目的是挖掘最频繁的模式。FP树的每个节点表示项集的一个项。根节点表示null,而较低的节点表示项集。在形成树的同时,保持节点与较低节点(即项集与其他项集)的关联
算法步骤
FP-growth算法的流程为:
首先构造FP树,然后利用它来挖掘频繁项集。
在构造FP树时,需要对数据集扫描两遍,第一遍扫描用来统计频率,第二遍扫描至考虑频繁项集。
算法案例
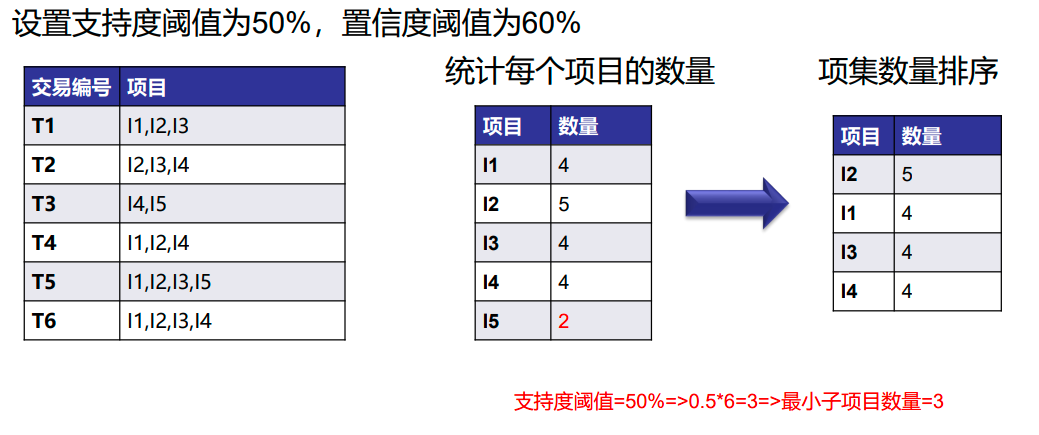


再次扫描数据库并检查事务。检查第一个事务并找出其中的项集。计数最大的项集在顶部,计数较低的下一个项集,以此类推。这意味着树的分支是由事务项集按计数降序构造的。

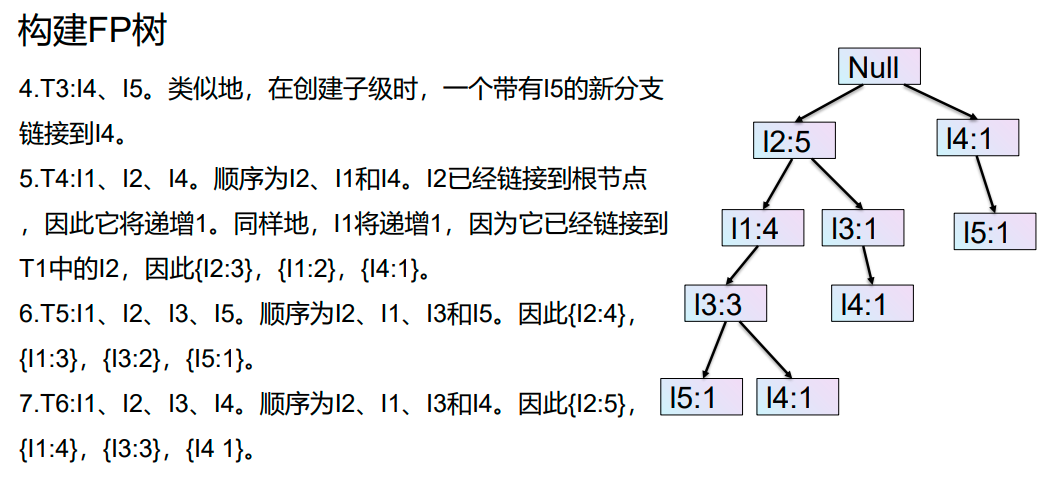
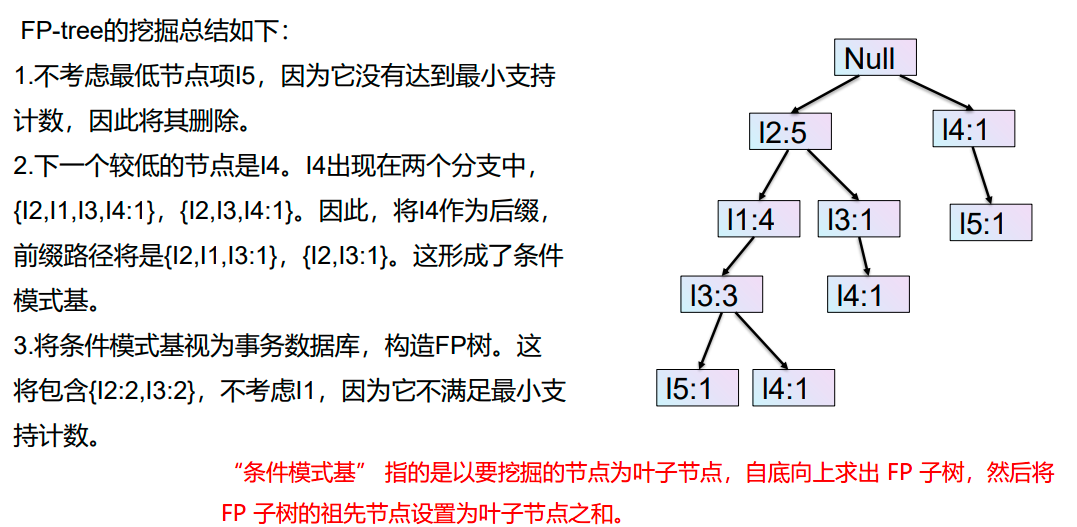
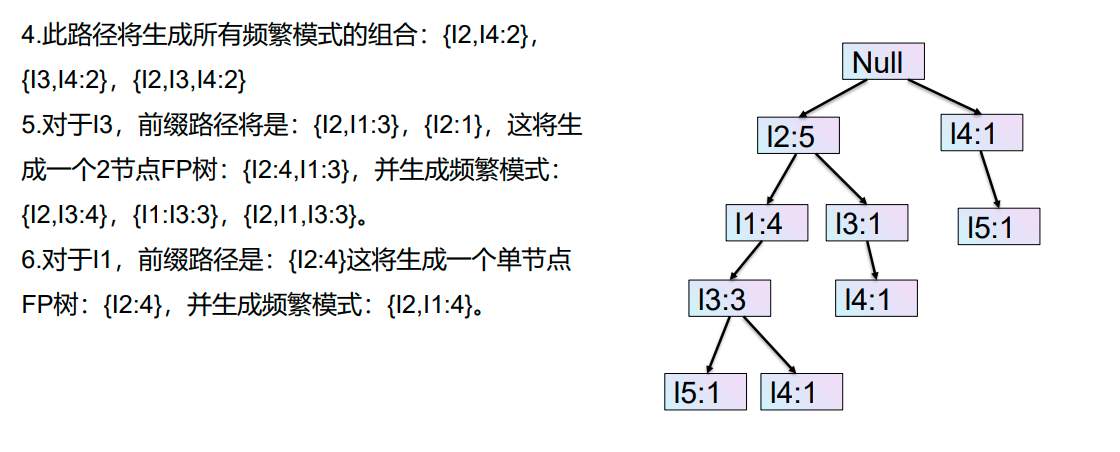
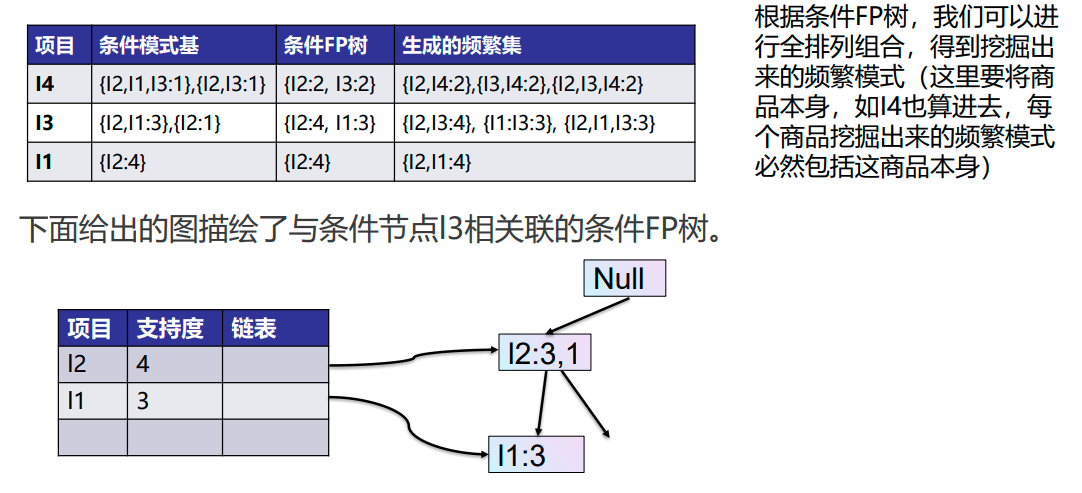
FP-Growth算法的优缺点
- 优点
1.与Apriori算法相比,该算法只需对数据库进行两次扫描
2.该算法不需要对项目进行配对,因此速度更快。
3.数据库存储在内存中的压缩版本中。
4.对长、短频繁模式的挖掘具有高效性和可扩展性。 - 缺点
1.FP-Tree比Apriori更麻烦,更难构建。
2.可能很耗资源。
3.当数据库较大时,算法可能不适合共享内存
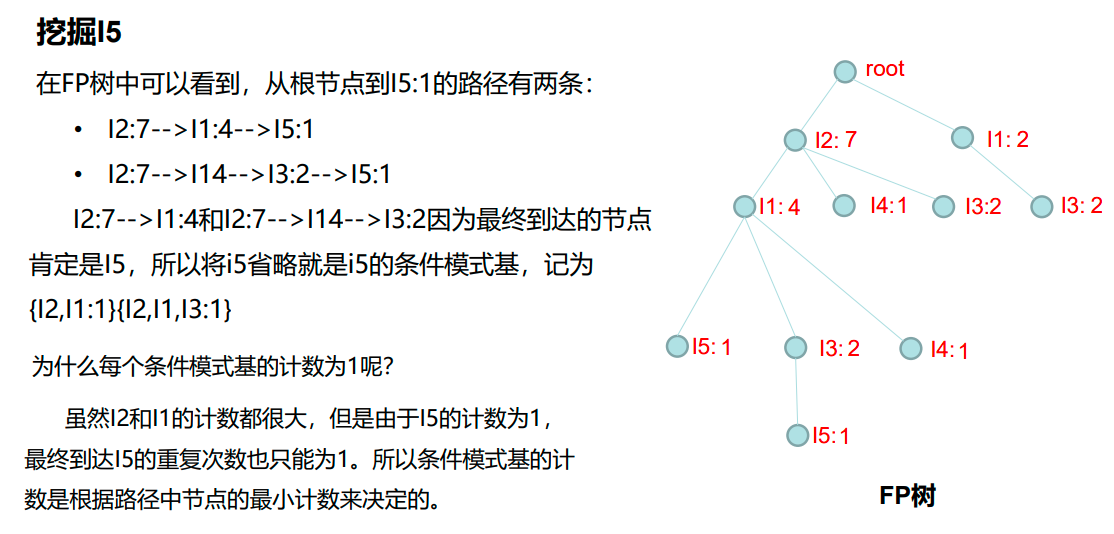
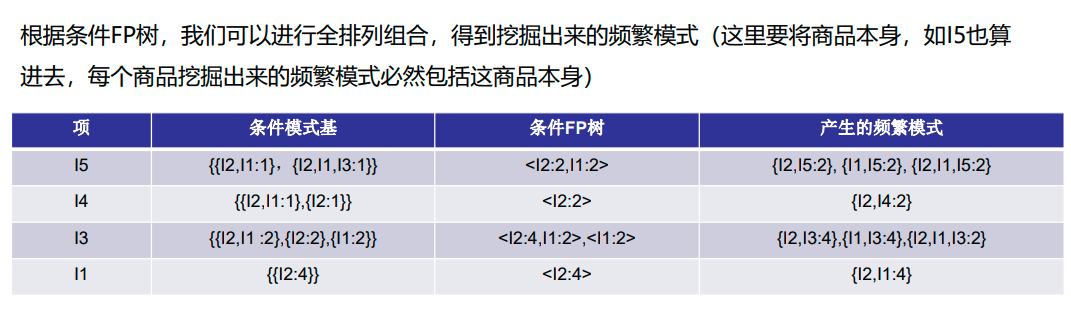
算法案例
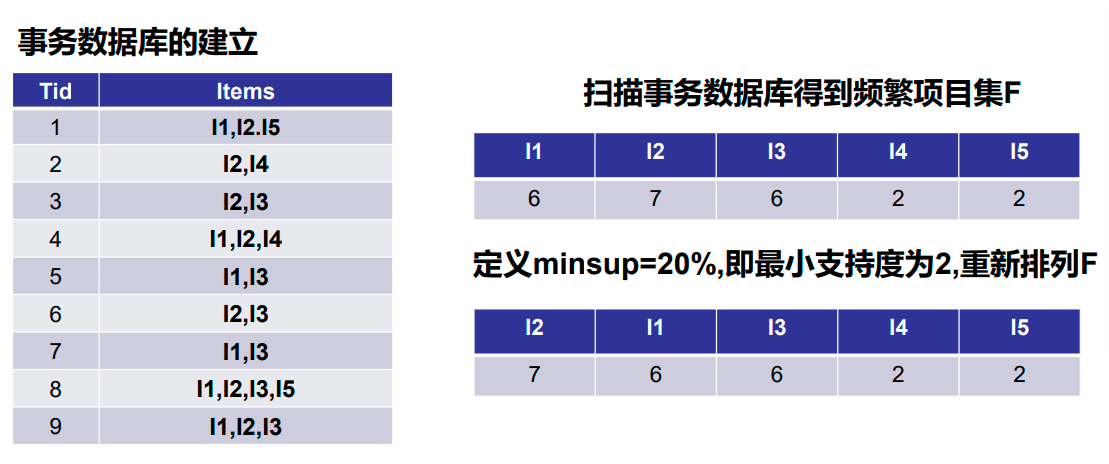
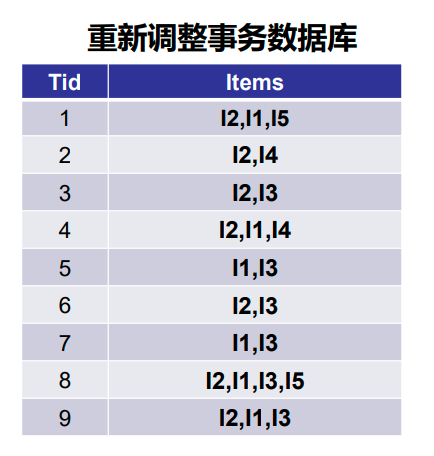




![[ai笔记10] 关于sora火爆的反思](https://img-blog.csdnimg.cn/img_convert/19faf9180a010ed24109295b5c16a7c3.png)


![[office] EXCEL怎么制作大事记图表- #学习方法#其他](https://img-blog.csdnimg.cn/img_convert/4da21016c26200855505d9d7541ad3f9.jpeg)