蓝桥杯DP算法——背包问题（C++）

news2024/11/28 16:44:12

目录

一、01背包问题

二、完全背包问题

三、多重背包问题

四、多重背包问题（优化版）

五、分组背包问题

一、01背包问题

01背包问题就是有N件物品，一个空间大小为V的背包，每个物品只能使用一次，使得背包中所装物品的价值总和最大。

  如图所示使用一个二维数组来存放从前i个物品中取，总体积不超过j的包中价值最大值。

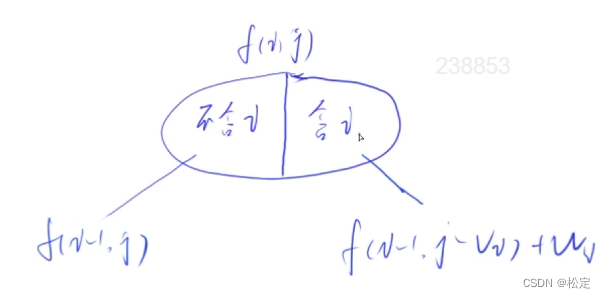
 根据图二所示，我们可以将每次dp到的情况分为两种，一种是选择第 i 件物品，另一种是不选择第 i 件物品。

  • （不含 i ）就是从0~i-1中选择体积不超过 j 的物品，也就是f(i-1,j)
  • （含 i ）即从 1 ~ i 中选，包含 i，且总体积不超过 j。可以先把第 i 个物品拿出来，即从第 1 ~ i-1中选，且总体积不超过 j-v[i]，也就是f(i-1,j-v_{i})+w_{i}

最终：f[ i ][ j ] = max(f[ i-1 ][ j ], f[i-1][j-v[ i ]] +w[ i ]

例题：https://www.acwing.com/problem/content/2/

朴素做法： 

#include<iostream>
using namespace std;
const int N=1010;
int v[N],w[N];
int f[N][N];

int main()
{
    int n,m;
    cin>>n>>m;
    
    for(int i =1;i<=n;i++) cin>>v[i]>>w[i];
    
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            f[i][j]=f[i-1][j];
            if(j>=v[i])//可以装的下
            {
                f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);
            }
        }
    }
    
    
    cout<<f[n][m];
    
    return 0;
}

优化： 

 f[i] 只用到了 f[i-1] 这一层，即 f[i-2] 到 f[0] 对 f[i] 是没有用的，所以第二层循环可以直接从 v[i] 开始

for (int i = 1; i <= n; i++) {
    for (int j = v[i]; j <= m; j++) {
        f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
    }
}

 从二维优化成一维（空间优化）

如果直接删除掉 f[i] 这一维即

f[j] = max(f[j], f[j-v[i]] + w[i]);

但是这样直接删掉是错误，因为j是递增的。

原式：f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);

改成一维：f[j] = max(f[j], f[j - v[i]] + w[i]);

由于 f[i][] 只跟上一状态（f[i - 1][]）有关 上面两个式子 ：这一状态（左） = 上一状态（右）

即 f[i][j] 是由 f[i - 1][j - v[i]] 推出来的 现在进行空间优化，那么必须要保证 f[j] 要由 f[j - v[i]] 推出来的。

如果j层循环是递增的，则相当于 f[i][j] 变得是由 f[i][j - v[i]] 推出来的， 而不是 f[i - 1][j - v[i]] 推出来的。

优化后代码：

#include<iostream>
using namespace std;
const int N=1010;
int v[N],w[N];
int f[N];

int main()
{
    int n,m;
    cin>>n>>m;
    
    for(int i =1;i<=n;i++) cin>>v[i]>>w[i];
    
    for(int i=1;i<=n;i++)
    {
        for(int j=m;j>=v[i];j--)
        {
                f[j]=max(f[j],f[j-v[i]]+w[i]);
        }
    }
    
    
    cout<<f[m];
    
    
    return 0;
}

二、完全背包问题

完全背包不同于01背包的是，每件物品都是无限使用的。

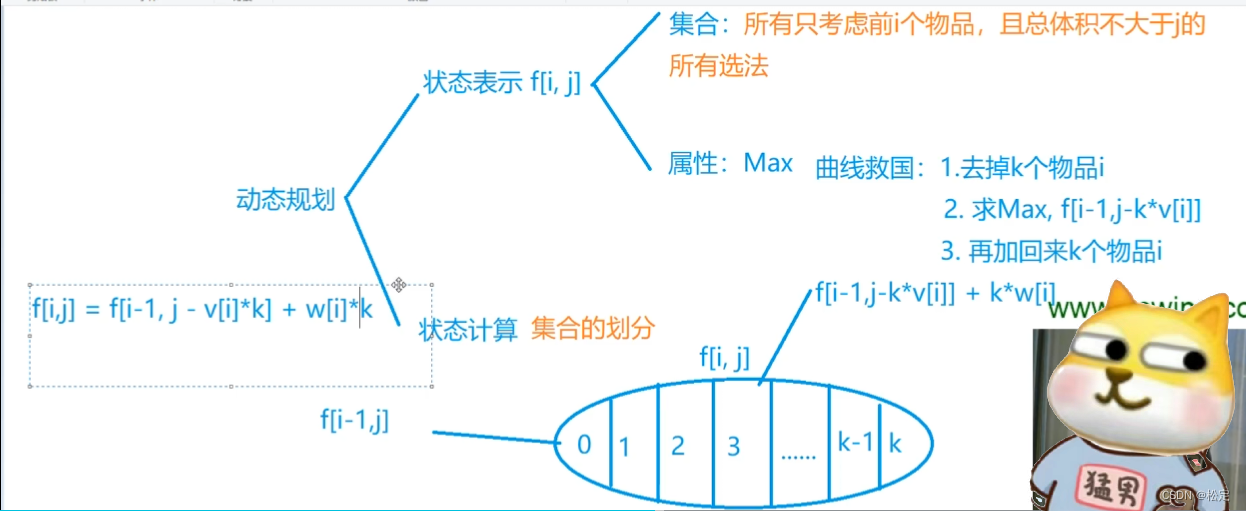
如图所示，与01背包相似的是每次选择0,1,2,3,4,5，....k个

不选时仍是 f[ i-1][ j ]

选择k件时是 f[ i-1][ j-k*v[i]] +k*w[i]

也就是：

                                                         f[ i-1][ j-k*v[i]] +k*w[i]

 例题：https://www.acwing.com/problem/content/3/

朴素写法： 

#include<iostream>
using namespace std;

const int N=1010;
int n,m;
int v[N],w[N],f[N][N];

int main()
{
    cin>>n>>m;
    for(int i=i;i<=n;i++) scanf("%d%d",&v[i],&w[i]);
    
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            for(int k=0;k*v[i]<=j;k++)
            {
                f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+w[i]*k);
            }
        }
    }
    
    cout<<f[n][m];
    return 0;
}

优化：

在对完全背包问题优化时，我们由图公式可知f[i][j]可以简化为max(f[i-1][j],f[i][j-v]+w)

优化后代码：

#include <iostream>
#include <algorithm>

using namespace std;

const int N=1010;
int f[N];
int v[N],w[N];
int n,m;
int main()
{
    cin>>n>>m;

    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];

    for(int i=1;i<=n;i++)
    {
        for(int j=v[i];j<=m;j++)
        {
            f[j]=max(f[j],f[j-v[i]]+w[i]);
        }
    }

    cout<<f[m];

    return 0;
}

三、多重背包问题

多重背包问题相较于之前的问题就是每个物品是有限s个。 

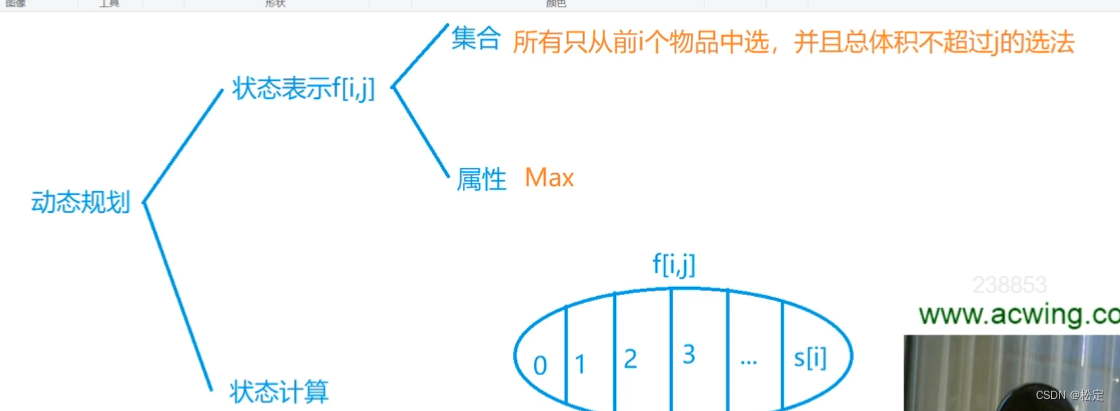
例题：https://www.acwing.com/problem/content/4/

#include<iostream>
using namespace std;
const int N=110;

int n,m;
int s[N],v[N],w[N];
int f[N][N];

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i]>>s[i];
    
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
            for(int k=0;k<=s[i]&&j>=(k*v[i]);k++)
            {
                    f[i][j]=max(f[i][j],f[i-1][j-v[i]*k]+w[i]*k);
            }
        }
        
    }
    cout<<f[n][m];
    return 0;
}

四、多重背包问题（优化版）

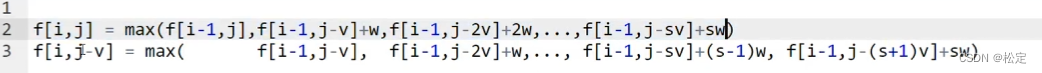
首先我们以之前完全背包问题的优化方法尝试使用另一个表达式来代替，但是结果如图所示，不是很好解决。 

二进制法优化：二进制优化的方法在于使用二进制的表示方式来代替每个物品的个数，当某件物品的个数很多的时候无需从1遍历循环到n，可以将其分解成log_{_{2}^{}}^{n}个位权来表示。

为了方便理解举个例子：

如果要拿1001次苹果，传统就是要拿1001次；二进制的思维，就是拿7个箱子就行（分别是装有512、256、128、64、32、8、1个苹果的这7个箱子）,这样一来，1001次操作就变成7次操作就行了。

但是要注意的一点是如果某件物品的个数不是二次幂减一，就将前一位的值与s差值记为下一个位权。这样就可以表示0~s之内的所有数了。

然后就将问题分解成为了，01背包问题。

例题：https://www.acwing.com/problem/content/5/

#include<iostream>
using namespace std;

const int N=11010,M=2010;
int v[N],w[N];
int f[N];

int main()
{
    int n,m;
    cin>>n>>m;
    
    int cnt=0;
    while(n--)//初始化v[] w[]
    {
        int a,b,s;
        cin>>a>>b>>s;
        int k=1;
        while(k<=s)
        {
            cnt++;
            v[cnt]=a*k;
            w[cnt]=b*k;
            s-=k;
            k*=2;
        }
        
        if(s>0)
        {
            cnt++;
            v[cnt]=a*s;
            w[cnt]=b*s;
        }
        
        
    }
    n=cnt;
    //01背包
    for(int i=1;i<=n;i++)
    {
        for(int j=m;j>=v[i];j--)
        {
            f[j]=max(f[j],f[j-v[i]]+w[i]);
        }
    }
    
    cout<<f[m];
    return 0;
}

五、分组背包问题

分组背包问题的不同于之前背包问题的地方在于分组背包是将物品分成几组，然后再在每组里面选择一个物品，并且每组只能选择一个物品。

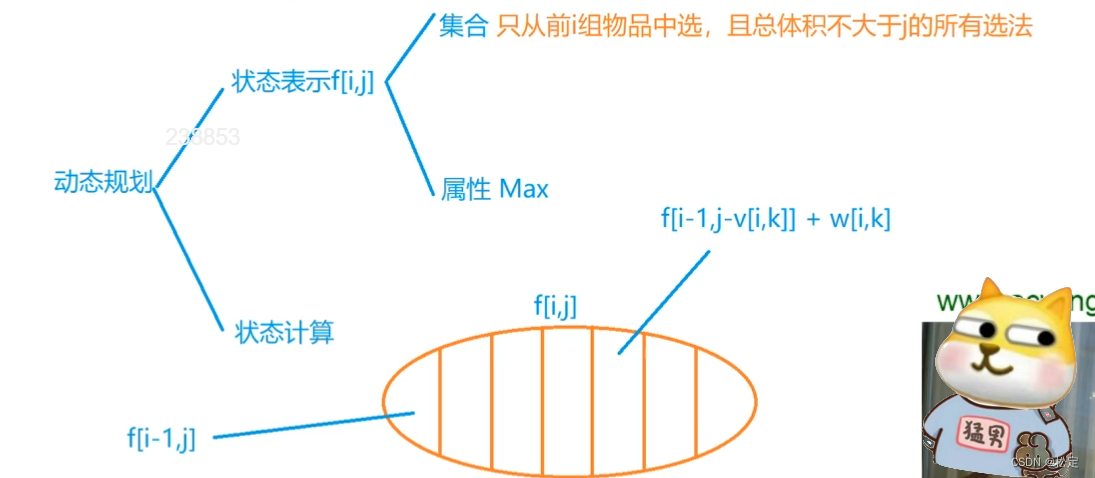
这里的dp状态计算与之前的也有所不同，这里表示的是第i组选哪一个，f[i-1][j]是表示不选择这一组的物品，f[i-1][j-v[i,k]]+w[i,k]表示的是这一组中选择哪一个。 

例题： https://www.acwing.com/problem/content/9/

#include<iostream>
using namespace std;

const int N=110;
int n,m;
int s[N],v[N][N],w[N][N];
int f[N];

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>s[i];
        for(int j=1;j<=s[i];j++)
        {
            cin>>v[i][j]>>w[i][j];
        }
    }
    
    for(int i=1;i<=n;i++)
    {
        for(int j=m;j>=0;j-- )
        {
            for(int k=0;k<=s[i];k++)
            {
                if(v[i][k]<=j)
                {
                    f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);
                }
            }
        }
    }
    
    
    cout<<f[m];
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1456028.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【软考高级信息系统项目管理师--第十五章：项目风险管理】

【软考高级信息系统项目管理师--第十五章：项目风险管理】

&#x1f680; 作者 &#xff1a;“码上有前” &#x1f680; 文章简介 &#xff1a;软考高级–信息系统项目管理师 &#x1f680; 欢迎小伙伴们 点赞&#x1f44d;、收藏⭐、留言&#x1f4ac; 第十五章&#xff1a;项目风险管理 风险的属性风险的分类风险管理过程规划风险管理…
阅读更多...
企业大宽带服务器用哪里最合适

企业大宽带服务器用哪里最合适

如今&#xff0c;数字经济的发展速度不断加快&#xff0c;进入数字化跑道的企业&#xff0c;每天都在大量输出、共享、存储数字内容&#xff0c;想要更高效、安全地让用户看到内容&#xff0c;企业的服务器需要满足大带宽、低延时、高并发等要求。 中小企业受限于资金、资源等…
阅读更多...
CTA量化策略—基于时间窗口的唐奇安通道法CTA策略

CTA量化策略—基于时间窗口的唐奇安通道法CTA策略

结合唐奇安通道法的核心思想&#xff0c;以及窗口法寻找到的局部高峰点和低谷点&#xff0c;将高点回归得到拟合直线作为上轨&#xff0c;取代唐奇安通道法 中的平行线上轨&#xff0c;同理也将低点回归得到拟合直线作为下轨&#xff0c;以此构建道氏理论 CTA策略。 回测标的&a…
阅读更多...
anomalib1.0学习纪实-续3：结合python lightning理思路

anomalib1.0学习纪实-续3：结合python lightning理思路

一、python lightning python lightning是个好东西&#xff0c;但不见得那么友好。 GPT4给我讲解了他的用法&#xff1a; 二、anomalib的思路 1、 创建一个Lightning Module。 首先&#xff0c;在src\anomalib\models\components\base\anomaly_module.py中&#xff0c; cl…
阅读更多...
基于Java SSM框架实现电影售票系统项目【项目源码】

基于Java SSM框架实现电影售票系统项目【项目源码】

基于java的SSM框架实现电影售票系统演示 SSM框架 当今流行的“SSM组合框架”是Spring SpringMVC MyBatis的缩写&#xff0c;受到很多的追捧&#xff0c;“组合SSM框架”是强强联手、各司其职、协调互补的团队精神。web项目的框架&#xff0c;通常更简单的数据源。Spring属于…
阅读更多...
生成式 AI - Diffusion 模型的数学原理（3）

生成式 AI - Diffusion 模型的数学原理（3）

来自 论文《 Denoising Diffusion Probabilistic Model》&#xff08;DDPM&#xff09; 论文链接&#xff1a; https://arxiv.org/abs/2006.11239 Hung-yi Lee 课件整理 文章目录 一、图像生成模型本质上的共同目标二、最大似然估计三、和VAE的关联四、概率计算 一、图像生成模…
阅读更多...
LeetCode.590. N 叉树的后序遍历

LeetCode.590. N 叉树的后序遍历

题目 590. N 叉树的后序遍历 分析 我们之前有做过LeetCode的 145. 二叉树的后序遍历&#xff0c;其实对于 N 叉树来说和二叉树的思路是一模一样的。 二叉树的后序遍历是【左 右 根】 N叉树的后序遍历顺序是【孩子 根】&#xff0c;你可以把二叉树的【左 右 根】想象成【孩子…
阅读更多...
MySQL为什么改进LRU算法？

MySQL为什么改进LRU算法？

普通LRU算法 LRU = Least Recently Used（最近最少使用）: 就是末尾淘汰法，新数据从链表头部加入，释放空间时从末尾淘汰. 当要访问某个页时，如果不在Buffer Pool，需要把该页加载到缓冲池,并且把该缓冲页对应的控制块作为节点添加到LRU链表的头部。当要访问某个页时，如果在…
阅读更多...
js设计模式:代理模式

js设计模式:代理模式

作用: 创建代理的数据来复刻对原有数据的操作,并且可以添加自己的逻辑 vue中的data就是用的代理模式,比较经典 示例: let proxyFun (obj)>{return new Proxy(obj,{get:(obj,prop,value)>{return obj[prop]},set:(obj,prop,value)>{obj[prop] valuereturn true}})…
阅读更多...
从阿里宜搭到吉客云通过接口配置打通数据

从阿里宜搭到吉客云通过接口配置打通数据

从阿里宜搭到吉客云通过接口配置打通数据 来源系统:阿里宜搭 宜搭是阿里巴巴自研的低代码应用搭建平台&#xff0c;传统情况下需要2周才能搭建完成的应用&#xff0c;用宜搭2小时就可完成。宜搭于2019年3月上线&#xff0c;用户可以在可视化界面上以拖拉拽的方式编辑和配置页面…
阅读更多...
【漏洞复现-通达OA】通达OA report_bi存在前台SQL注入漏洞

【漏洞复现-通达OA】通达OA report_bi存在前台SQL注入漏洞

一、漏洞简介 通达OA（Office Anywhere网络智能办公系统）是由北京通达信科科技有限公司自主研发的协同办公自动化软件，是与中国企业管理实践相结合形成的综合管理办公平台。通达OA为各行业不同规模的众多用户提供信息化管理能力，包括流程审批、行政办公、日常事务、数据统计…
阅读更多...
二叉树和N叉数的遍历合集

二叉树和N叉数的遍历合集

二叉树和N叉数的遍历合集 二叉树的前序遍历 前序遍历的顺序是 根 -> 左儿子 -> 右儿子&#xff0c;所以我们直接按照这个顺序 dfs 就行 dfs class Solution { public:vector<int> preorderTraversal(TreeNode* root) {vector<int> res;function<void(…
阅读更多...
如何在极低成本硬件上落地人工智能算法 —— 分布式AI

如何在极低成本硬件上落地人工智能算法 —— 分布式AI

一、背景 分布式AI的发展前景非常广阔&#xff0c;随着5G、6G等高速网络通信技术的普及和边缘计算能力的提升&#xff0c;以及AI算法和硬件的不断优化进步&#xff0c;分布式AI将在多个领域展现出强大的应用潜力和市场价值&#xff1a; 1. **物联网&#xff08;IoT&#xff0…
阅读更多...
unity学习（20）——客户端与服务器合力完成注册功能（2）调试注册逻辑

unity学习（20）——客户端与服务器合力完成注册功能（2）调试注册逻辑

接着上一节的问题&#xff0c;想办法升级成具备数据库功能的服务器&#xff0c;这个是必须的。 至少在初始化要学会把文件转换为session&#xff0c;新知识&#xff0c;有挑战的。 现在是从LoginHandler.cs跳到了AccountBiz.cs的create&#xff0c;跳度还是很大的。 create函…
阅读更多...
宝塔安装MySQL、设置MySQL密码、设置navicat连接

宝塔安装MySQL、设置MySQL密码、设置navicat连接

1、登录宝塔面板进行安装 2、设置MySQL连接密码 3、安装好了设置navicat连接 登录MySQL [roothecs-394544 ~]# mysql -uroot -p Enter password: 切换到MySQL数据 mysql> use mysql Database changed mysql> 查询用户信息 mysql> select host,user from user; ---…
阅读更多...
一起玩儿物联网人工智能小车（ESP32）——63 SD和TF卡模块的使用

一起玩儿物联网人工智能小车（ESP32）——63 SD和TF卡模块的使用

摘要&#xff1a;本文介绍SD和TF卡模块的使用方法 前面介绍了非易失性存储的使用方法&#xff0c;由于空间和本身只支持键值对的限制&#xff0c;非易失性存储只适用于少量数据的记录。而不适用于各种声音、图片、大量数据等情况的使用。这时候就需要有文件系统或者更大容量存…
阅读更多...
无人机数据链技术，无人机数据链路系统技术详解，无人机数传技术

无人机数据链技术，无人机数据链路系统技术详解，无人机数传技术

早期的无人机更多的为军事应用服务&#xff0c;如军事任务侦查等&#xff0c;随着技术和社会的发展&#xff0c;工业级无人机和民用无人机得到快速的发展&#xff0c;工业级无人机用于农业植保、地理测绘、电力巡检、救灾援助等&#xff1b;民用无人机用于航拍、物流等等领域。…
阅读更多...
Unity之闪电侠大战蓝毒兽

Unity之闪电侠大战蓝毒兽

目录 &#x1f3a8;一、创建地形 &#x1f3ae;二、创建角色 &#x1f3c3;2.1 动画 &#x1f3c3;2.2 拖尾 &#x1f3c3;2.3 角色控制 ​&#x1f3c3;2.4 技能释放 &#x1f3c3;2.5 准星 &#x1f4f1;三、创建敌人 &#x1f432;3.1 选择模型 &#x1f432;3.…
阅读更多...
GitLab安装配置

GitLab安装配置

一、GitLab的简介 GitLab是开源的代码托管平台&#xff0c;提供版本控制功能、代码审查、持续集成等工具&#xff0c;帮助团队协作开发软件项目。用户可以创建仓库存储代码&#xff0c;管理问题追踪&#xff0c;部署自动化流程等。 二、GitLab的安装 1、Rocky_Linux 下载安装 …
阅读更多...
使用RK3588开发板使用 SFTP 互传-windows与开发板互传

使用RK3588开发板使用 SFTP 互传-windows与开发板互传

MobaXterm 软件网盘下载路径&#xff1a;“iTOP-3588 开发板\02_【iTOP-RK3588 开发板】开发资料\04_iTOP-3588 开发板所需 PC 软件&#xff08;工具&#xff09;\02-MobaXterm”。 打开 MobaXterm 创建一个 SFTP 会话&#xff0c;如下图所示&#xff1a; 输入密码 topeet 进入…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023