二叉树和N叉数的遍历合集
二叉树的前序遍历
前序遍历的顺序是 根 -> 左儿子 -> 右儿子,所以我们直接按照这个顺序 dfs 就行
dfs
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> res;
function<void(TreeNode*)> dfs = [&](TreeNode* u) -> void {
if (!u) return;
res.emplace_back(u->val);
dfs(u->left);
dfs(u->right);
};
dfs(root);
return res;
}
};
时间复杂度 : O ( n ) O(n) O(n) (每个节点至多被遍历一次)
二叉树的中序遍历
中序遍历的顺序是 左儿子 -> 根 -> 右儿子,所以我们直接按照这个顺序 dfs 就行
dfs
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
function<void(TreeNode*)> dfs = [&](TreeNode* u) -> void {
if (!u) return;
dfs(u->left); // 左
res.push_back(u->val); // 根
dfs(u->right); // 右
};
dfs(root);
return res;
}
};
时间复杂度 : O ( n ) O(n) O(n) (每个节点至多被遍历一次)
迭代法
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
if (!root) return {};
vector<int> res;
stack<TreeNode*> stk;
stk.push(root);
unordered_map<TreeNode*, bool> st;
TreeNode* t = nullptr;
while (stk.size()) {
t = stk.top();
while (!st[t->left] && t->left) {
stk.push(t->left);
t = t->left;
}
res.push_back(t->val);
st[t] = true;
stk.pop();
if (!st[t->right] && t->right) {
stk.push(t->right);
t = t->right;
}
}
return res;
}
};
时间复杂度 : O ( n ) O(n) O(n) (每个节点至多被遍历一次)
二叉树的后序遍历
后序遍历的顺序是 左儿子 -> 右儿子 -> 根,所以我们直接按照这个顺序 dfs 就行
dfs
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> res;
function<void(TreeNode*)> dfs = [&](TreeNode* u) -> void {
if (!u) return;
dfs(u->left);
dfs(u->right);
res.push_back(u->val);
};
dfs(root);
return res;
}
};
时间复杂度 : O ( n ) O(n) O(n) (每个节点至多被遍历一次)
二叉树的层序遍历
层序遍历就是一层一层遍历,我们只需要用一个数组存一下每一层的所有节点,每次遍历更新为该层节点的所有子节点就行,本质是 bfs
bfs
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
if (!root) return {};
vector<TreeNode*> q{root};
vector<vector<int>> res;
while (q.size()) {
vector<TreeNode*> p;
vector<int> t;
for (auto& x : q) {
t.push_back(x->val);
for (auto& node : {x->left, x->right}) {
if (node) {
p.push_back(node);
}
}
}
res.push_back(t);
q = move(p);
}
return res;
}
};
时间复杂度 : O ( n ) O(n) O(n) (每个节点至多被遍历一次)
二叉树的垂序遍历
给你二叉树的根结点
root,请你设计算法计算二叉树的 垂序遍历 序列。对位于
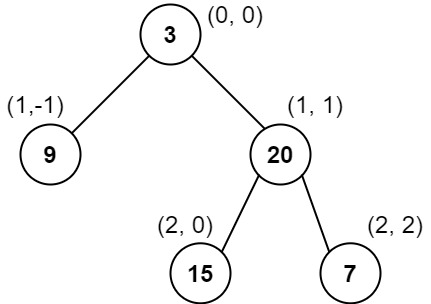
(row, col)的每个结点而言,其左右子结点分别位于(row + 1, col - 1)和(row + 1, col + 1)。树的根结点位于(0, 0)。二叉树的 垂序遍历 从最左边的列开始直到最右边的列结束,按列索引每一列上的所有结点,形成一个按出现位置从上到下排序的有序列表。如果同行同列上有多个结点,则按结点的值从小到大进行排序。
返回二叉树的 垂序遍历 序列。
提示:
- 树中结点数目总数在范围
[1, 1000]内0 <= Node.val <= 1000示例 1:
输入:root = [3,9,20,null,null,15,7] 输出:[[9],[3,15],[20],[7]] 解释: 列 -1 :只有结点 9 在此列中。 列 0 :只有结点 3 和 15 在此列中,按从上到下顺序。 列 1 :只有结点 20 在此列中。 列 2 :只有结点 7 在此列中。
根据题目的意思,我们只需要将所有的信息存下来,最后排序即可,然后将所有的数据分组,返回答案即可,我们要记录3个数据,每个节点的{深度, 编号, 值},因为超过了两个数据,我们不能用pair<int, int>,我们可以使用元组,tuple<int, int, int>,最后分组一下即可
dfs
class Solution {
public:
using TIII = tuple<int, int, int>;
vector<vector<int>> verticalTraversal(TreeNode* root) {
vector<TIII> pos;
function<void(TreeNode*, int, int)> dfs = [&](TreeNode* u, int dep, int id) -> void {
pos.push_back({id, dep, u->val});
if (u->left) dfs(u->left, dep + 1, id - 1);
if (u->right) dfs(u->right, dep + 1, id + 1);
};
dfs(root, 0, 0);
sort(pos.begin(), pos.end(), [&](TIII& a, TIII& b) {
if (get<0>(a) != get<0>(b)) return get<0>(a) < get<0>(b);
else if (get<1>(a) != get<1>(b)) return get<1>(a) < get<1>(b);
return get<2>(a) < get<2>(b);
});
vector<vector<int>> res;
for (int i = 0; i < pos.size(); ) {
vector<int> t;
int j = get<0>(pos[i]), k = i;
// 分组
while (k < pos.size() && get<0>(pos[k]) == j) {
t.push_back(get<2>(pos[k ++]));
}
res.push_back(t);
i = k;
}
return res;
}
};
时间复杂度 : O ( n ) O(n) O(n)
N叉树的前序遍历
和二叉树的前序遍历思路一样的,稍微改一改就行
dfs
class Solution {
public:
vector<int> preorder(Node* root) {
vector<int> res;
function<void(Node*)> dfs = [&](Node* u) -> void {
if (!u) return;
res.emplace_back(u->val);
for (auto& x : u->children) {
dfs(x);
}
};
dfs(root);
return res;
}
};
时间复杂度: O ( n ) O(n) O(n) (每个节点之被遍历一次)
N叉树的后序遍历
同
class Solution {
public:
vector<int> postorder(Node* root) {
vector<int> res;
function<void(Node*)> dfs = [&](Node* u) -> void {
if (!u) return;
for (auto& x : u->children) {
dfs(x);
}
res.emplace_back(u->val);
};
dfs(root);
return res;
}
};
时间复杂度: O ( n ) O(n) O(n) (每个节点之被遍历一次)
N叉树的层序遍历
同二叉树
dfs
class Solution {
public:
vector<vector<int>> levelOrder(Node* root) {
if (!root) return {};
vector<Node*> q{root};
vector<vector<int>> res;
while (q.size()) {
vector<Node*> p;
vector<int> t;
for (auto& x : q) {
t.push_back(x->val);
for (auto& node : x->children) {
p.push_back(node);
}
}
res.push_back(t);
q = move(p);
}
return res;
}
};
时间复杂度: O ( n ) O(n) O(n) (每个节点之被遍历一次)
结束了