目录
鉴别
1 报文鉴别
1.1 用数字签名进行鉴别(原理)
可保证机密性的数字签名
1.2 密码散列函数
MD5 算法
MD5 算法计算步骤
安全散列算法 SHA-1
1.3 用报文鉴别码实现报文鉴别
用报文鉴别码 MAC 鉴别报文
使用已签名的报文鉴别码 MAC 对报文鉴别
2 实体鉴别
最简单的实体鉴别过程
使用不重数进行鉴别
使用公钥体制进行不重数鉴别
假冒攻击
中间人攻击
鉴别
·鉴别 (authentication) 是网络安全中一个很重要的问题。
鉴别包括:

1 报文鉴别

1.1 用数字签名进行鉴别(原理)

鉴别发送者: A 用其私钥 SKA 对报文 X 进行 D 运算得到的密文。B 为了核实签名,用 A 的公钥 PKA 进行 E 运算,还原出明文 X。
鉴别报文: 由于无法得到并使用 A 的私钥 SKA 对报文 X 进行 D 运算,B 对收到的报文进行核实签名的 E 运算将会得出不可读的明文,可以发现报文已被篡改过。
不可否认: A 要抵赖曾发送报文给 B,B 可把 X 及 D_SK_A(X) 出示给进行公证的第三者。第三者很容易用 PKA去证实 A 确实发送 X 给 B。
数字签名的三个功能:
1.实体鉴别:证明来源。
2.报文鉴别:防篡改,保证完整性。
3.不可否认:防抵赖。
关键:没有其他人能够持有 A 的私钥 SKA。
可保证机密性的数字签名
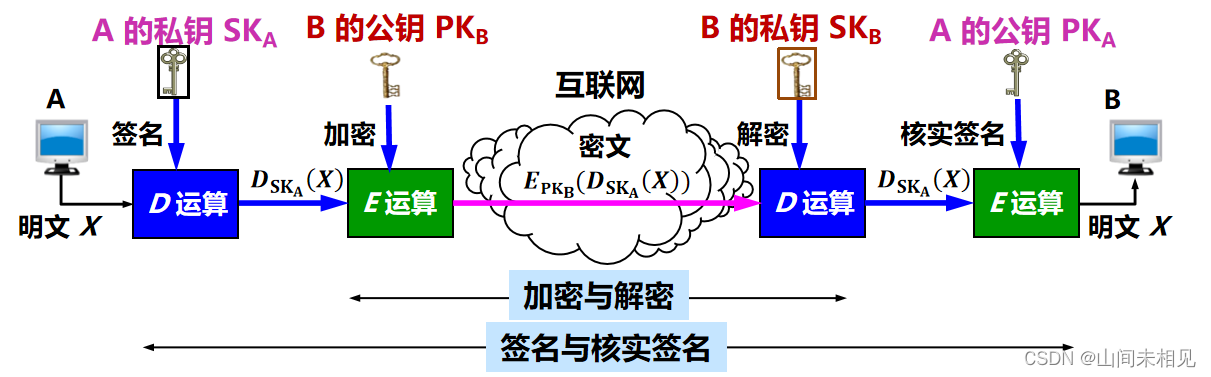
·先后进行两次 D 运算和两次 E 运算,运算量太大,花费非常多的 CPU 时间。目前普遍使用开销小得多的对称密钥加密。
·要实现数字签名必须使用公钥密码,但一定要设法减小公钥密码算法的开销。
1.2 密码散列函数
·散列函数(又称为杂凑函数,哈希函数)在计算机领域中广泛使用。
·符合密码学要求的散列函数又常称为密码散列函数 (cryptographic hash function)。
·密码散列函数 H(X) 应具有以下四个特点:
1.结果的长度应较短和固定。
2.应具有很好的抗碰撞性,避免不同的输入产生相同的输出。
3.应是单向函数(one-way function),不能逆向变换。
4.其他特性:输出的每一个比特都与输入的每一个比特有关;仅改动输入的一个比特,输出也会相差极大;包括许多非线性运算等。
密码散列函数是单向的:

实用的单向密码散列函数:
·MD5:Message Digest 5,报文摘要的第 5 个版本。
·SHA-1:Secure Hash Algorithm,安全散列算法。
·SHA-1 比 MD5 更安全,但计算起来却比 MD5 要慢些。
·1995 年发布的新版本 SHA-1 [RFC 3174] 在安全性方面有了很大的改进。
MD5 算法
·MD5 的设计者 Rivest 曾提出一个猜想:
根据给定的 MD5 报文摘要代码,要找出一个与原来报文有相同报文摘要的另一报文,其难度在计算上几乎是不可能的。
·基本思想:用足够复杂的方法,使报文摘要代码中的每一位都与原来报文中的每一位有关。
MD5 算法计算步骤
1.附加:把任意长的报文按模 计算其余数(64位),追加在报文的后面。
2.填充:在报文和余数之间填充 1~512 位,使得填充后的总长度是 512 的整数倍。填充的首位是 1,后面都是 0。
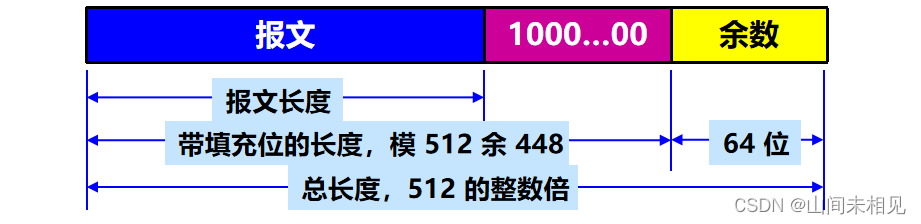
3.分组:把追加和填充后的报文分割为多个 512 位的数据块,每个 512 位的报文数据再分成 4 个 128 位的数据块。
4.计算:将 4 个 128 位的数据块依次送到不同的散列函数进行 4 轮计算。每一轮又都按 32 位的小数据块进行复杂的运算。一直到最后计算出 MD5 报文摘要代码(128 位)。
在2004年,中国学者王小云发表了轰动世界的密码学论文,证明可以用系统的方法找出一对报文,这对报文具有相同的 MD5 报文,而这仅需 15 分钟,或不到 1 小时。MD5 的安全性就产生了动摇。随后,又有许多学者开发了对 MD5 实际的攻击。MD5 最终被安全散列算法 SHA 标准所取代。
安全散列算法 SHA-1
·安全散列算法 SHA (Secure Hash Algorithm):由美国标准与技术协会 NIST 提出的一个散列算法系列。
·和 MD5 相似,但其散列值的长度为 160 位。
·SHA-1 也是先把输入报文划分为许多 512 位长的数据块,然后经过复杂运算后得出散列值。
但 SHA-1 后来也被证明其实际安全性并未达到设计要求,并且也曾被王小云教授的研究团队攻破。谷歌也宣布了攻破 SHA-1 的消息。许多组织都已纷纷宣布停用 SHA-1。
·SHA-1 已被 SHA-2、SHA-3 所替代。
·SHA-2 的多种变型: SHA-224,SHA-256,SHA-384,SHA-512。
·SHA-3 的多种变型: SHA3-224,SHA3-256,SHA3-384,SHA3-512。
·SHA-3 采用了与 SHA-2 完全不同的散列函数。
目前,密码学家尚无法把一个任意已知的报文 X,篡改为具有同样 MD5 或 SHA-1 散列值的另一报文 Y。
1.3 用报文鉴别码实现报文鉴别
·散列函数问题:可以防篡改,但不能防伪造,不能真正实现报文鉴别。

·解决方法:采用报文鉴别码 MAC。
把双方共享的密钥 K 与报文 X 进行拼接,然后进行散列运算。 散列运算得出的结果为固定长度的 H(X + K),称为报文鉴别码 MAC (Message Authentication Code)。
用报文鉴别码 MAC 鉴别报文

·只要入侵者不掌握密钥 K,就无法伪造 A 发送的报文(因为无法伪造 A 的 MAC)。
·鉴别过程并没有执行加密算法,消耗的计算资源少。
这样的报文鉴别码称为数字签名或数字指纹。
HMAC 与 MAC 不同
MAC:
·把密钥 K 作为计算 MAC 的参数。
·可以使用多种计算 MAC 的算法。

HMAC (Hashed MAC):
·把密钥 K 拼接在明文后面。
·使用密码散列算法对其进行运算。
·得出的散列值就是 HMAC。

使用已签名的报文鉴别码 MAC 对报文鉴别
·问题:如何分发共享密钥 K?
·解决:采用公钥系统。

·没有对报文进行加密,而是对很短的散列 H(X) 进行 D 运算。
·入侵者没有 A 的私钥,因此不可能伪造出 A 发出的报文。

2 实体鉴别
·实体鉴别与报文鉴别不同。
·报文鉴别:对每一个收到的报文都要鉴别报文的发送者。
·实体鉴别:在系统接入的全部持续时间内,对和自己通信的对方实体只需验证一次。
最简单的实体鉴别过程
·使用共享的对称密钥 KAB 实现实体鉴别。
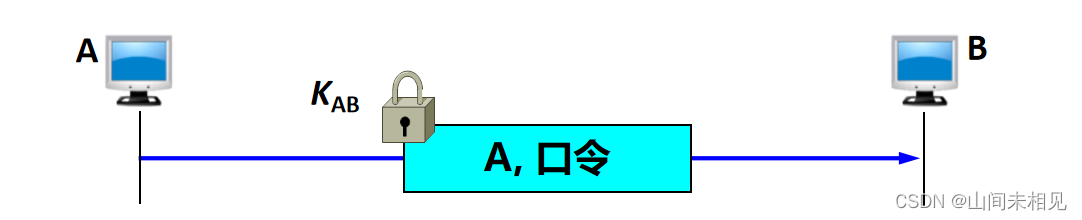
存在明显漏洞:不能抵抗重放攻击。
重放攻击 (replay attack):入侵者 C 不需要破译报文,而是直接把由 A 加密的报文发送给 B,使 B 误认为 C 就是 A。B 就会向伪装成 A 的 C 发送许多本来应当发给 A 的报文。
使用不重数进行鉴别
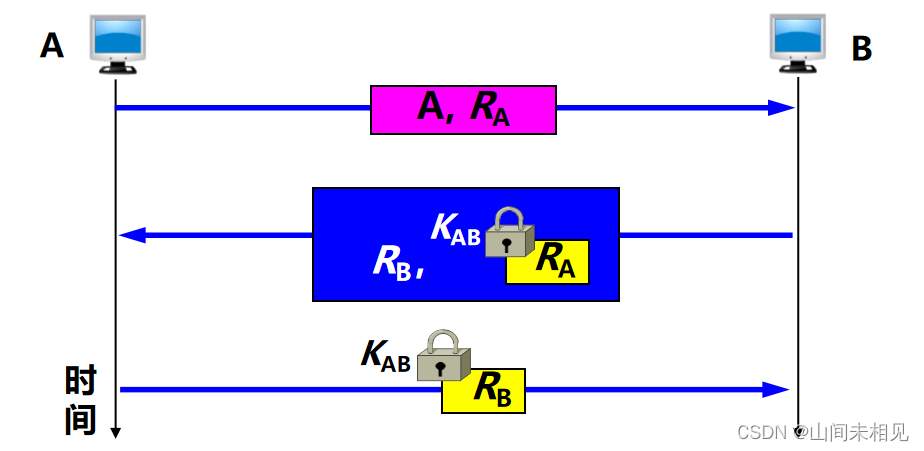
·不重数 (nonce) :是一个不重复使用的大随机数,即“一次一数”。
·由于不重数不能重复使用,所以 C 在进行重放攻击时无法重复使用所截获的不重数。
使用公钥体制进行不重数鉴别

·在使用公钥密码体制时,可以对不重数进行签名鉴别。
·使用公钥核实签名。
假冒攻击
·C 冒充是 A,发送报文给 B,说:“我是 A”。
·B 选择一个不重数 RB,发送给 A,但被 C 截获了。
·C 用自己的私钥 SKC 冒充是 A 的私钥,对 RB 加密,并发送给 B。
·B 向 A 发送报文,要求对方把解密用的公钥发送过来,但这报文也被 C 截获了。
·C 把自己的公钥 PKC 冒充是 A 的公钥发送给 B。
·B 用收到的公钥 PKC 对收到的加密的 RB 进行解密,其结果当然正确。
·于是 B 相信通信的对方是 A,接着就向 A 发送许多敏感数据,但都被 C 截获了。
中间人攻击
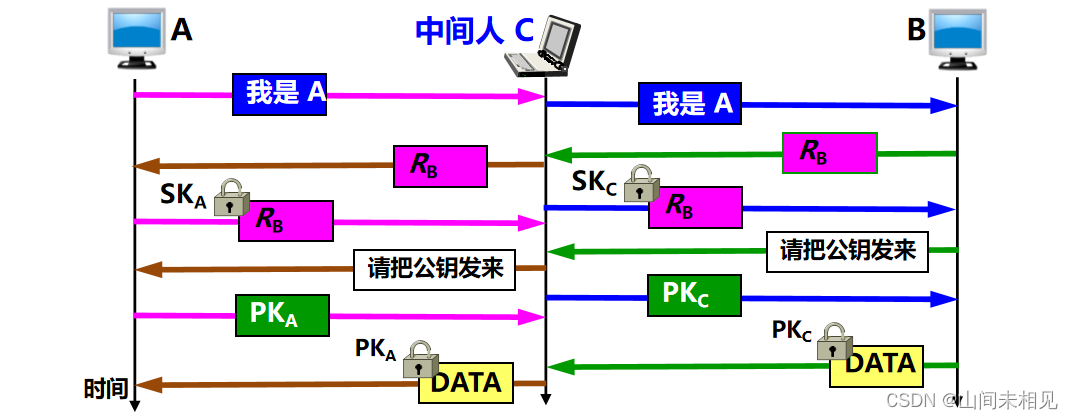
·可见,公钥的分配以及认证公钥的真实性是一个非常重要的问题。
欢迎一起学习~