1. 合并二叉树
617. 合并二叉树
https://leetcode.cn/problems/merge-two-binary-trees/
给你两棵二叉树： root1 和 root2 。
想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。
示例 1：
输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出：[3,4,5,5,4,null,7]示例 2：
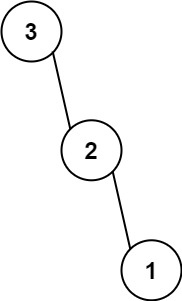
输入：root1 = [1], root2 = [1,2]
输出：[2,2]解题思路
第一想法还是我比较熟悉的递归思路，两棵树的结合的特别之处只是在于一个树有的节点，另一个没有，所以终止条件会有所区别。来考虑下递归的三要素。
- 参数和返回值：两个树的节点root1和root2；当前递归内已经收到底部返回值后已经集合后的node节点
- 终止条件：root1和root2都为null
- 递归逻辑：把root1和root2进行结合，把root1和root2的左节点进行递归作为返回值的左孩子，把root1和root2的右节点进行递归作为返回值的右孩子
代码
class Solution {
public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
if (root1 == null && root2 == null)
return null;
int val1 = 0, val2 = 0;
TreeNode left1 = null, left2 = null, right1 = null, right2 = null;
if (root1 != null) {
val1 = root1.val;
left1 = root1.left;
right1 = root1.right;
}
if (root2 != null) {
val2 = root2.val;
left2 = root2.left;
right2 = root2.right;
}
TreeNode root = new TreeNode(val1 + val2);
root.left = mergeTrees(left1, left2);
root.right = mergeTrees(right1, right2);
return root;
}
}2. 二叉搜索树中的搜索
700. 二叉搜索树中的搜索https://leetcode.cn/problems/search-in-a-binary-search-tree/
给定二叉搜索树（BST）的根节点 root 和一个整数值 val。
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 null 。
示例 1:
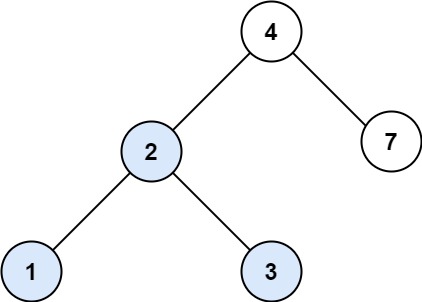
输入：root = [4,2,7,1,3], val = 2
输出：[2,1,3]示例 2:
输入：root = [4,2,7,1,3], val = 5
输出：[]解题思路
这道题只是考察是否掌握二叉搜索树的定义和搜索，只需要从根节点一路循环下去，找到了就返回，如果循环完都没找到就返回null。
代码
class Solution {
public TreeNode searchBST(TreeNode root, int val) {
while (root != null) {
if (root.val == val)
return root;
else if (root.val > val)
root = root.left;
else
root = root.right;
}
return null;
}
}3. 验证二叉搜索树
98. 验证二叉搜索树https://leetcode.cn/problems/validate-binary-search-tree/
给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下：
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1：
输入：root = [2,1,3]
输出：true示例 2：
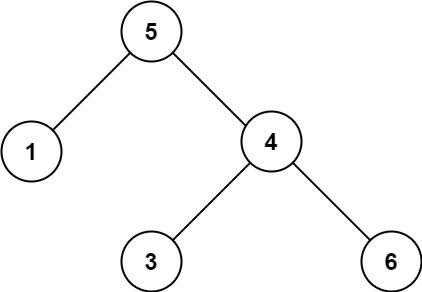
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。解题思路
验证二叉搜索树也就是对所有节点进行一个遍历，同时进行一个判断，对每一个节点来说，左右子树是二叉搜索树，并且大于左子树的值小于右子树的值，就满足二叉搜索树的定义。
这个思路是可以进行递归的，所以考虑递归的三要素进行递归实现：
- 参数和返回值：参数为一个root节点表示当前遍历到的节点，一个bool类型的表示是否为二叉搜索树
- 终止条件：root为null的时候，说明子树满足条件，返回true
- 递归逻辑：递归逻辑内比较难的地方在于，左子树的最大值和右子树的最小值用来比较后，如果这个root是父节点的左孩子，又要得到右子树的最大值，如果是右孩子，要得到左子树的最小值。需要一个好的递归逻辑避免这个不一致情况。所以可以拆分成两个步骤，先判断左子树，然后比较max和root的val，比较完后，max就变成了root，然后判断右子树，在判断右子树的过程中，max也在变，由于右子树是最后判断的，所以一定能得到最右下的一个节点，那就是最大值。得到后，回溯的时候就又是max了。
代码
class Solution {
TreeNode max;
public boolean isValidBST(TreeNode root) {
if (root == null) {
return true;
}
// 左
boolean left = isValidBST(root.left);
if (!left) {
return false;
}
// 中
if (max != null && root.val <= max.val) {
return false;
}
max = root;
// 右
boolean right = isValidBST(root.right);
return right;
}
}
