目录
一、二叉树性质
1、满二叉树、完全二叉树
2、平衡二叉树
3、不平衡二叉树
二、二叉树的存储
1、普通做法
2、竞赛做法
三、二叉树的遍历
1、宽度优先遍历
2、深度优先遍历
(1)先(根)序遍历
(2)中(根)序遍历
(3)中(根)序遍历的特点(⭐)
(4)后(根)序遍历
(5)三种遍历的关系
3、例题1——完全二叉树的权值(2019年省赛,lanqiaoOJ题号183)
4、例题2——FBI树(lanqiaoOJ题号571)
(1)普通做法
(2)竞赛做法
一、二叉树性质
- 每个结点最多有两个子节点:左孩子、右孩子。以它们为根的子树称为左子树、右子树。
- 二叉树的第 i 层,最多有 2^i-1 个节点。
- 二叉树的每个节点不必全有左、右孩子,可以只有一个孩子或没有孩子,没有孩子的结点称为叶子节点。
1、满二叉树、完全二叉树
【满二叉树】
如果每一层的结点数都是满的,称为满二叉树。

【完全二叉树】
如果满二叉树只在最后一层有缺失,并且缺失的编号都在最后,那么称为完全二叉树。

几乎完美的平衡二叉树。
2、平衡二叉树
- 在平衡二叉树上能进行极高效率的访问。例如满二叉树或完全二叉树,二叉树每一层的结点数量按 2 的倍数递增,能极快地扩展到很大的范围。
- 一棵有 N 个结点的满二叉树,树的高度是 O(logN)。从根结点到叶子结点,只需要走 logN 步,例如 N =100万,树的高度仅有 20,只需要 20 步就能到达 100 万个结点中的任意一个。
- 高级数据结构 ≈ 基于二叉树的数据结构(666)
3、不平衡二叉树
- “链状” 二叉树。
- 每一层都缺失很多结点,退化成一个长链条状。
- 失去了二叉树天然的优势。
- 只有在平衡的二叉树上才能进行高效的操作。
- 不平衡的二叉树退化成了线性结构,和低效的链表没多大区别。
二、二叉树的存储
1、普通做法
class node:
def __init__(self,s,l=None,r=None):
self.val=None #节点的值
self.l=l #指向左右孩子的存储位置
self.r=r2、竞赛做法
- 为了编码简单,加快速度,一般用静态数组来实现二叉树。
- 定义一个大小为 N 的静态结构体数组,用它存一棵二叉树。
- 定义静态数:tree=['']*10000
- 根节点:tree[1]
- 节点 tree[p] 的左子节点:tree[2*p]
- 节点 tree[p] 的右子节点:tree[2*p+1]
三、二叉树的遍历
1、宽度优先遍历

宽度优先遍历:一层层地遍历二叉树,用队列实现。
出队列的顺序是:EBGADFICH。按层次深度逐层输出。

2、深度优先遍历
- 先 (根) 序遍历
- 中 (根) 序遍历
- 后 (根) 序遍历
(1)先(根)序遍历

def postorder(p):
print(tree[p],end='')
if tree[2*p]!='':
postorder(2*p)
if tree[2*p+1]!='':
postorder(2*p+1)
- 按父、左儿子、右儿子的顺序访问:
- EBADCGFIH
- 先序遍历的第一个结点是根
(2)中(根)序遍历
def postorder(p):
if tree[2*p]!='':
postorder(2*p)
print(tree[p],end='')
- 按左儿子、父、右儿子的顺序访问:
- ABCDEFGHI
- 结果为什么是字典序?
(3)中(根)序遍历的特点(⭐)
- ABCDEFGHI
- 返回的结果:根结点左边的点都在左子树上,右边的都在右子树上。
- 例如:E是根, E左边的 “ABCD” 在它的左子树上;
- 例如:在子树 “ABCD” 上,B 是子树的根,那么“A”在它的左子树上, “CD”在它的右子树上。
(4)后(根)序遍历
def postorder(p):
if tree[2*p]!='':
postorder(2*p)
if tree[2*p+1]!='':
postorder(2*p+1)
print(tree[p],end='')
- 按左儿子、右儿子、父的顺序访问
- ACDBFHIGE
- 后序遍历的最后一个结点是根
(5)三种遍历的关系
- 已知二叉树的:“中序遍历+先序遍历”,或者 “中序遍历+后序遍历”,都能确定一棵树。
- 但是只有“先序遍历+后序遍历”,不能确定一棵树。例如左图,它们的先序遍历都是"1 2 3",后序遍历都是"3 2 1"。
3、例题1——完全二叉树的权值(2019年省赛,lanqiaoOJ题号183)
【题目描述】
给定一棵包含 N 个节点的完全二叉树,树上每个节点都有一个权值,按从上到下、从左到右的顺序依次是 A1, A2, …, AN。现在小明要把相同深度的节点的权值加在一起,他想知道哪个深度的结点权值之和最大?如果有多个深度的权值和同为最大,请你输出其中最小的深度。注:根的深度是1。
【输入描述】
第一行包含一个整数 N (1<=N<=10^5) 。第二行包含 N 个整数 A1, A2, ... , AN (-10^5 <= Ai <=10^5)
【输出描述】
一个整数表示答案。
【输入样例】
7
1 6 5 4 3 2 1
【输出样例】
2
p=[]
for i in range(0,33): # 32层
p.append(2**i) # 每层的个数:p[]=1,2,4,8,16,...
n=int(input())
a=input().split(" ")
sum=[0]*32 # 记录每层的和
for i in range(0,n):
for j in range(0,len(p)):
if i+1>=p[j] and i+1<=p[j+1]: # 计算每层的和
sum[j]+=int(a[i])
maxx,mindeep=-1,-1
for i in range(0,len(sum)):
if maxx<sum[i]:
maxx,mindeep=sum[i],i
print(mindeep+1)
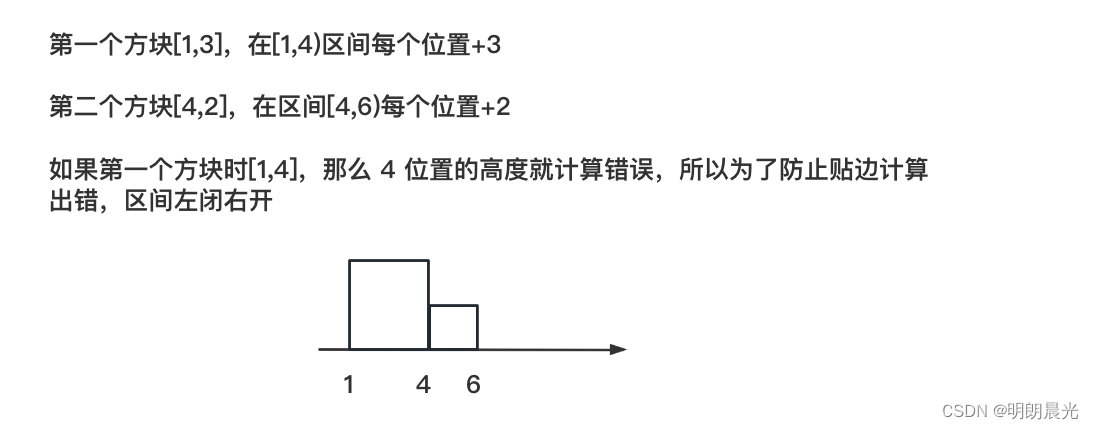
- 一棵完全二叉树
- 第一层1个,第2层2个,第3层4个,... ,
- 最后第 k 层最多 2^(k-1) 个
- 第 i 层存储第 2^(i-1) 个到第 (2^i)-1 个数。
4、例题2——FBI树(lanqiaoOJ题号571)
【题目描述】
我们可以把由 “0” 和 “1” 组成的字符串分为三类:全 “0” 串称为 B 串,全 “1” 串称为 I 串,既含 “0” 又含 “1” 的串则称为 F 串。FBI树是一种二叉树,它的结点类型也包括 F 结点,B 结点和 I 结点三种。由一个长度为 2^N 的 “01” 串 S 可以构造出一棵 FBI 树 T,递归的构造方法如下:
1. T 的根结点为 R,其类型与串 S 的类型相同;
2. 若串 S 的长度大于 1,将串 S 从中间分开,分为等长的左右子串 S1 和 S2;由左子串 S1 构造 R 的左子树 T1,由右子串 S2 构造 R 的右子树 T2。
现在给定一个长度为 2^N 的 “01” 串,请用上述构造方法构造出一棵 FBI 树,并输出它的后序遍历序列。
【输入描述】
第一行是一个整数 N (0<=N<=10)。第二行是一个长度为 2^N 的 “01” 串。
【输出描述】
输出一个字符串,即 FBI 树的后序遍历序列。
【输入样例】
3
10001011
【输出样例】
IBFBBBFIBFIIIFF
- 用满二叉树来存题目的 FBI 树,满二叉树用静态数组实现。题目 N = 10 时,串的长度是 2N = 1024 ,有 1024 个元素,需要建一棵大小为 4096 的二叉树 tree[4096]。
- 题目要求建一棵满二叉树,从左到右的叶子结点就是给定的串 S,并且把叶子结点按规则赋值为字符F、B、I,它们上层的父结点上也按规则赋值为字符F、B、I。
- 最后用后序遍历打印二叉树。
- 下面演示两种做法:普通做法、竞赛做法
(1)普通做法
节点用数据结构表示,用 l、r 分别指向左右子节点
class node:
def __init__(self,s,l=None,r=None):
self.val=None
self.l=l
self.r=r
if '0' in s and '1' in s:
self.val='F'
elif '0' in s:
self.val='B'
else:
self.val='I'
def bulid(s):
if len(s)==1:
return node(s)
if len(s)==0:
return None
root=node(s,bulid(s[:len(s)>>1]),bulid(s[len(s)>>1:]))
return root
def postorder(root):
if root:
postorder(root.l)
postorder(root.r)
print(root.val,end='')
else:
return
n=int(input())
s=list(input())
root=bulid(s)
postorder(root)
(2)竞赛做法
用一维数组存二叉树
def bulid_FBI(p,left,right):
if left==right:
if s[right]=='1':
tree[p]='I'
else:
tree[p]='B'
return
mid=(left+right)//2
bulid_FBI(2*p,left,mid)
bulid_FBI(2*p+1,mid+1,right)
if tree[2*p]=='B' and tree[2*p+1]=='B':
tree[p]='B'
elif tree[2*p]=='I' and tree[2*p+1]=='I':
tree[p]='I'
else:
tree[p]='F'
def postorder(p):
if tree[2*p]!='':
postorder(2*p)
if tree[2*p+1]!='':
postorder(2*p+1)
print(tree[p],end='')
n=int(input())
s=input()
tree=['']*4400
bulid_FBI(1,0,len(s)-1)
postorder(1)
以上,基础数据结构——二叉树
祝好