具有自主、多鳍和仿生机器人的鱼类三维游泳(2021)
原文链接:https://iopscience.iop.org/article/10.1088/1748-3190/abd013
这是一篇仿生机器鱼的设计,该论文从鱼的仿生结构到具体的一部分电路设计都有非常详细的介绍,鱼的尺寸大小仅有手掌大小。
摘要
鱼类会迁徙相当长的距离,并表现出非凡的灵活性来躲避捕食者和食物。与机器人系统相比,鱼类的游泳性能和机动性仍然是无与伦比的,部分原因是以前的工作集中在机器人和拍打翼系统上,这些系统要么庞大复杂,要么拴在外部致动器和电源上。相比之下,我们展示了一个机器人——Finbot——它结合了高度的自主性、可操作性和仿生性以及微型尺寸(
160
c
m
3
160 \ \rm cm^3
160 cm3)。因此,它非常适合于在封闭的实验室试验床上进行鱼类游泳的受控三维实验。Finbot使用四个独立可控的鳍和感官反馈来实现精确的闭环水下运动。不同的尾鳍可以磁性连接,以重新配置鳍机器人,使其以最高速度(
122
m
m
s
−
1
≡
1
B
L
s
−
1
122 \ \rm mm\ s^{-1} ≡ 1 \ \rm BL\ s^{-1}
122 mm s−1≡1 BL s−1)或最低的运输成本(
C
o
T
=
8.2
CoT = 8.2
CoT=8.2)在Strouhal数低至0.53的情况下游泳。我们用12种不同的尾鳍进行了150多次实验,以测量游水鱼的三个关键特征:(I)线性速度-频率关系,(ii) U形CoT,和(iii)反向卡门尾流(用粒子图像测速术可视化)。在帆布床较低的地方,出现了更多的鱼状尾流。通过复制自主的多鳍鱼类游泳,Finbot缩小了鱼类和鱼类机器人之间的差距,并可以解决水生运动中的公开问题,例如新鱼类机器人的优化推进,或控制鱼类节能的流体动力学原理。
关键词:水下机器人,鱼游泳,多鳍,自主,机动,粒子图像测速
1.简介
鱼是优秀的游泳者,在诸如珊瑚礁这样的混乱环境中寻找食物,在海洋中长距离迁徙,或者逆流而上繁殖后代。在这样做的时候,鱼结合了高度的机动性和有效的长距离游泳,这种结合从工程角度来看非常有吸引力。鱼类能够达到这种水平的表现,部分是因为它们使用多个鳍来引导三维力,并由感觉系统来支持运动学的闭环控制。具有高机动性、多鳍控制和有效巡航能力的仿生机器人将极大地扩展自主和自推进水下机器人的应用范围。
生物学家在理解水生运动方面取得了巨大的进步 [1,2]。许多鱼利用身体的波动来加速周围的流体向后运动,从而产生推进力 [1,3-6]。机身和尾部的振动通常会留下一串反向旋转的涡流,其相互作用会产生一股向后的流体射流,称为反向卡门尾流 [7]。当时间平均时,这个尾流显示了一个中心高速喷流,表明产生推力的拍击附体。射流的强度与游泳速度相关,并取决于旋涡脱落和尾巴跳动的频率。据观察,各种鱼类的游泳速度与它们的尾巴跳动频率大致成线性比例 [8,9]。
此外,当描述为运输成本(CoT)时,鱼通常表现出U形曲线的游泳能量学 [10-12] 。
C
o
T
(
=
P
/
m
g
U
)
CoT (= P/mgU)
CoT(=P/mgU)是无量纲的,此处定义为每体重的代谢功率
P
P
P,每游泳速度的
m
g
mg
mg,
U
U
U。此外,Strouhal数
S
t
(
=
f
A
/
U
)
St (= fA/U)
St(=fA/U) 是广泛使用的跳水运动有效性指标 [9,13]。St描述了游泳者每摆动一次尾巴前进的相对距离,A是尾巴摆动的幅度,以尾巴的尖端到尖端的偏移来测量。基于这些生物学观察,人们可以为机器人表现出鱼类般的游泳定义以下三个关键标准:(I)旋涡从拍打的尾鳍脱落,从而形成反向卡门尾流;(二)拍尾频率与游泳速度呈线性相关;和(iii) CoT是U形的,在中等游泳速度时最小。
对水生运动的洞察启发了机器人学家设计出类似鱼的推进器 [14–19] 和机器人系统 [20–41]。然而,许多工程系统无法精确模仿鱼类游泳或实现类似鱼类的性能,而是依赖于单鳍的开环控制。一类仿鱼实验平台是拍动推进器,由附在吃水线上方外部致动器上的单个鳍或翼组成 [14–17]。虽然作为简单的物理模型用于研究游泳性能(包括CoT [18,19] 等指标)非常有用,但与真正的鱼相比,这种推进器既不是自主的,也不是自由游泳的。另一组自动推进的鱼形机器人规模大且复杂 [20–22],设计用于在开放水域操作,而不是作为实验室的实验平台。用于实验室研究的机器人通常由安全带或绳索固定 [22–26,32] ,因为在足够小且可操作的设计中集成电源和传感自主性是一项挑战。尽管机动性受到限制,自由游动的绳系机器人仍可用于研究鱼类的运动。采用软驱动技术的系统大多动力不足,这使得产生类似鱼的游泳速度变得困难 [27–29] 。总的来说,很少有机器人是自主和自由游泳的 [20,21,27–31,33–38,42] ,或者像鱼一样 [20,25,30,31,33–38,42] 。通常,受鱼启发的机器人很难协调与鱼一样游泳相关的关键参数:自我推进、三维控制身体位置的能力、机动性和低成本有效的巡航。因此,在当前的设备空间中存在一个缺口:自主、可操纵和仿生的多鳍水下机器人[补充表S1(https://stacks . IOP . org/BB/16/026018/Mme dia)]。
本文的目标是用一个名为Finbot的仿生机器人(图1)演示鱼类游泳,包括U形运输成本和反向卡门尾流等特性。据我们所知,F**inbot是第一个也是最小的多鳍自主水下机器人,它也忠实地复制了鱼类游泳的多种特征。**虽然基于我们自己以前的工作 [30] ,Finbot进行了重大升级,增加了可交换的caudalfin、机载电源监控器和更流线型和仿生的身体形状,以支持这项研究。
2.方法
2.1 Finbot平台
Finbot增强了我们以前的工作 [30] 中提出的用于三维(3D)多鳍游泳的早期机器人。两个机器人都有四个可独立控制的鳍。两个胸鳍和一个尾鳍允许在水平的浪涌-摇摆平面内转动、停止和向前运动。这些水平运动由机载惯性测量单元(IMU)的传感反馈引导,与沿垂荡轴的垂直潜水解耦。机器人在滚动和俯仰方面是被动稳定的,并且具有轻微的正浮力,因此它们会向水面漂浮,除非使用压力传感器的深度估计值激活背鳍进行受控潜水。
在Finbot的设计中,我们专注于两个主要目标:(i)通过仔细选择能够产生反向卡门尾流结构的柔性尾鳍来产生类似鱼的运动;(ii)实现3D空间中的自推进和受控运动,其性能指标如速度和成本令人想起鱼类。在结果中,我们强调了Finbot的新功能,包括受蓝堂(肝旁副棘鸟,Paracanthurus hepatus)启发的更新的身体形状,用于更高性能和功耗监控的升级电子设备,以及用于测试不同尾鳍的模块化磁性机制。关于设计、部件和制造的附加信息见附录的第1节。
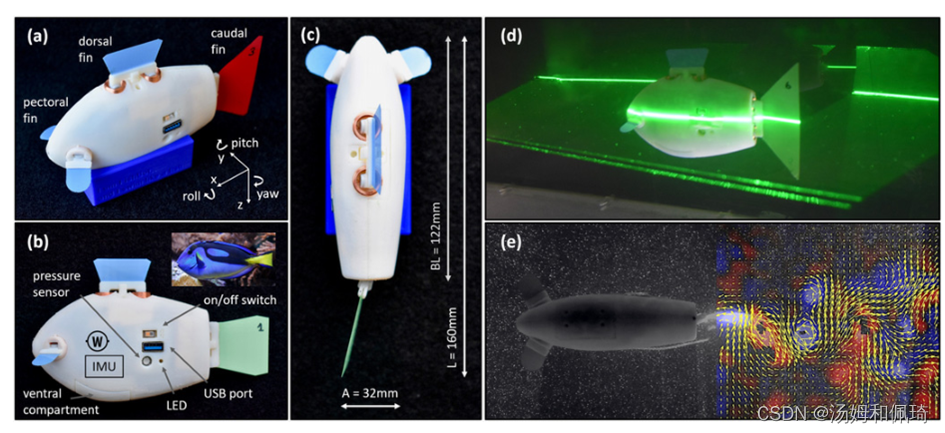
图 1 Finbot:自主仿生实验平台。(a) Finbot旨在能够像鱼一样自主游泳。四个可独立控制的柔性鳍能够在3D空间进行精确机动(x,y,z对应于浪涌、摇摆和起伏)。尾鳍磁性连接到主体,可以很容易地改变游泳速度和CoT。(b)坚硬的流线型车身的造型灵感来自蓝色唐鱼(如右上图4所示)。Finbot在3D中自主游泳,使用惯性传感器(IMU)控制航向,使用压力传感器控制深度,并可以监控自身的功耗。©根据多种鱼类的观察值,将尾拍振幅A调整为体长L(包括鳍)的大约20% [44] 。(d) Finbot利用粒子图像测速术进行激光成像,用于显示尾流结构。(e)鳍状机器人后面的拖尾尾流;几个尾流类似于逆向卡门街道,这是鱼类游泳的特征。
2.2 闭环控制的多鳍自由游泳
与大多数类似尺寸的水下机器人(补充表S1)相比,它具有高度的机动性,这使得鳍状机器人能够遵循大范围的3D轨迹,如我们之前所示 [30]。在这里,我们着重于水下直线游泳,尾鳍以恒定的频率工作,以产生浪涌方向的推力,而胸鳍用于通过影响绕偏航轴的转向来纠正任何偏离直线路线的情况。胸鳍的频率通过比例-积分-微分(PID)闭环控制器在2 Hz到8 Hz之间连续调节,以根据与直线轨迹的瞬时偏差调节推力(补充图S2)。从时间平均的IMU读数中检测这种偏差,由此机器人和IMU分别被初始化为与直线目标方向对准。使用实现的闭环控制器,Finbot可以保持水下直线航线。然而,由于IMU的偏航漂移约为 0.5 ° / m i n 0.5°/ min 0.5°/min,小误差会随着时间的推移而累积。有关控制器设计和深度控制的更多信息,请参见视频S3和附录的第2部分。
表S1
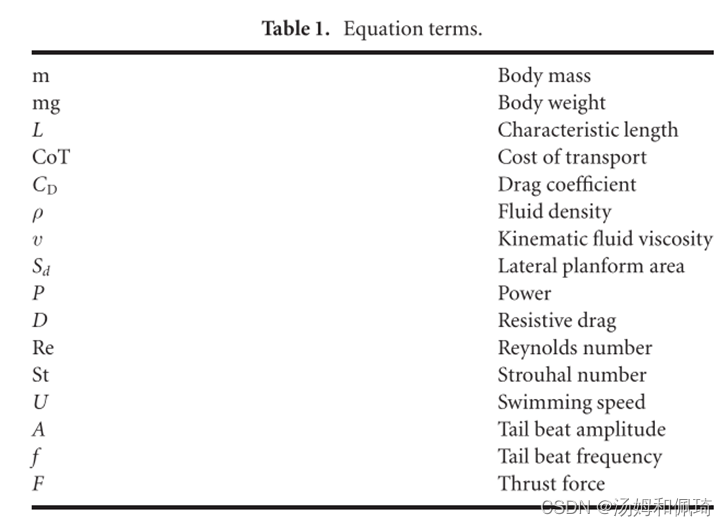
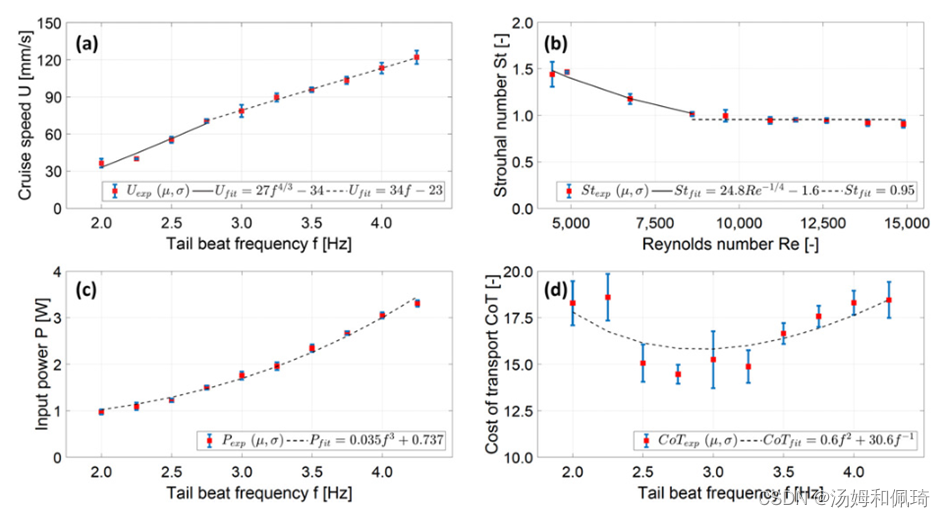
图2 Finbot的游泳性能。(a)对于大于
70
m
m
s
−
1
70\ \rm mm\ s^{-1}
70 mm s−1的速度,U与f成线性关系。低速时,U与
f
4
/
3
f^{4/3}
f4/3成比例。(b)因此,St向低速方向增加,向高速方向稳定在0.95。© P与f 3成正比,但当f = 0时,在静止时不为零。(d) CoT呈U形,在中频时最小。(a)–( d):使用28毫米× 36毫米× 22毫米(短底、长底、高)和0.19毫米厚的等腰梯形翼片。红色方块是N = 5次试验的平均值μ。蓝色误差线表示平均值的标准差σ,其中一些被红色方块遮住了。黑线代表拟合曲线。
2.3 各种尾拍频率和鳍几何形状的尾鳍
我们在不同的尾拍频率下测试了各种尾鳍,尾鳍振荡的振幅总是被机械地限制在尾脚的枢轴处。为了在所有频率上在不同鳍的尖端实现一致的峰-峰振幅,我们用脉宽调制来调节尾部致动器的输入功率。对于每个鳍和频率,我们在五种不同的输入功率下拍摄慢动作视频,以直观地选择功率设置,使鳍的峰间传播时间与规定的振荡周期最佳匹配。此外,我们选择了正弦输入信号,以增强输入功率最小的峰值振幅处方向的平滑变化,因此运动更加波动。
2.4.阻力和粒子图像测速仪的实验装置和测量设备
所有实验都是在实验室流动池 [3] 中的淡水中进行的,流动池由66 cm×28 cm×28cm(长、宽、高)的大型试验段组成(补充图S3(A))。除了调整PID控制器和测量机器人身体阻力的单独实验之外,水保持静止。阻力是在3D打印的机器人假人上测量的,该机器人假人连接到水线上方的六维力/扭矩传感器(ATI Nano17)。对于 30 m m s − 1 30\ \rm mm\ s^{-1} 30 mm s−1 至 200 m m s − 1 200\ \rm mm\ s^{-1} 200 mm s−1 范围内的六种不同流速中的每一种,以1000 Hz的采样速率采集120 s的数据,并在去除信号中的自相关后,对数据进行时间平均,得到单个平均值和标准偏差。我们用Photron Mini-UX100高速摄像机以250帧/秒 和1280×1024像素 的分辨率录制了实验视频。为了显示尾鳍脱落的旋涡和相应的尾流结构 ,在水中添加了微粒 (平均尺寸为50μm ),光引擎5W氩离子激光器与鲍威尔透镜一起产生了指向鳍状机器人的水平光幕。用DaVis 8.4软件(LaVision Inc .,Gö ttingen Germany)处理成对的连续视频帧,以生成贯穿尾拍周期的速度矢量场的时间序列。图1(e)和视频《S2》显示了被微粒包围并被激光照射的鳍状机器人,其尾迹清晰可见。
2.5.游泳速度和功耗的测试程序和数据处理
在所有实验中,Finbot 在水面上初始化,并在 66 cm 长测试段的右端与目标游泳方向对齐,持续 15 秒,在此期间测量稳态漂移和表面压力。然后,Finbot 在地表以下 15 厘米的编程目标深度处被小心地释放,并在 5秒到 22秒内游向测试部分的另一左端,具体取决于其巡航速度(视频S1和补充图S3)。对于图2-4,我们分别以每个尾拍频率重复测试运行 5 次和 3 次,并报告游泳性能指标的平均值和标准偏差借助深度卷积神经网络 [43] (补充3.1节),从记录的视频中推导出稳态巡航时的游泳速度,即初始加速期后的游泳速度。前进推进的功率消耗是用机载功率监视器以大约30 Hz的采样率测量的 (补充3.2节),因此只考虑尾鳍的输入功率。因此,我们报告的成本必须理解为尾鳍产生的向前推进的成本,而不是利用所有鳍的总成本。
2.6.对蓝鳃太阳鱼(Lepomis macrochirus)进行的活鱼实验
蓝鳃太阳鱼在一个再循环流动池中游动,在 0.5 B L s − 1 0.5\ \rm BL\ s^{-1} 0.5 BL s−1 至 2.5 B L s − 1 2.5\ \rm BL\ s^{-1} 2.5 BL s−1的速度范围内获得了关于稳定波动身体运动和尾迹流模式的数据。通过用小的(平均尺寸为12μm)镀银玻璃珠在水中播种,并通过使用Redlake MotionScope PCI 500高速摄像系统在250帧/秒和1/1000秒快门速度下对尾鳍尾流中的水流模式进行成像,来显现尾流模式。一台8 W氩离子连续波激光器(Coherent Inc .,Santa Clara,CA,USA)聚焦成一个薄光幕(1-2mm厚),照亮反射颗粒。我们使用DaVis 8.4软件,使用标准PIV算法进行交叉相关分析,与我们之前的研究相同。
2.7.速度、斯特劳哈尔数、阻力系数、功率和运输成本的比例定律
鱼和鳍状机器人在水上运动时遵循自然比例定律。在巡航状态下,尾翼产生的推力与机身受到的阻力平衡,因此St仅是机器人形状的函数,与流线型物体阻力系数的平方根  == [44]== 成比例,其中
== [44]== 成比例,其中 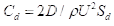 ,D为阻力,ρ为流体密度,
S
d
S_d
Sd为尾翼和机身的横向平面面积(表1定义了所有方程项)。对于低速层流状态,薄流线型物体的阻力系数大约为
R
e
−
1
/
2
Re^{-1/2}
Re−1/2 [44,45] ,其中
R
e
=
U
L
/
v
Re = UL/v
Re=UL/v 是雷诺数,L是游泳者的特征长度,v是流体的运动粘度。因此,对于恒定的重叠幅度,St的比例为
R
e
−
1
/
4
Re^{-1/4}
Re−1/4,U的比例为
f
4
/
3
f^{4/3}
f4/3。对于与湍流相关的高速,
C
d
C_d
Cd和St保持相对恒定 [44,45] ,U与f成线性比例关系。
,D为阻力,ρ为流体密度,
S
d
S_d
Sd为尾翼和机身的横向平面面积(表1定义了所有方程项)。对于低速层流状态,薄流线型物体的阻力系数大约为
R
e
−
1
/
2
Re^{-1/2}
Re−1/2 [44,45] ,其中
R
e
=
U
L
/
v
Re = UL/v
Re=UL/v 是雷诺数,L是游泳者的特征长度,v是流体的运动粘度。因此,对于恒定的重叠幅度,St的比例为
R
e
−
1
/
4
Re^{-1/4}
Re−1/4,U的比例为
f
4
/
3
f^{4/3}
f4/3。对于与湍流相关的高速,
C
d
C_d
Cd和St保持相对恒定 [44,45] ,U与f成线性比例关系。
根据无粘流体力学理论,并由实验数据支持 [46,47] ,对于纯俯仰翼型(作为尾翼的替代物),输入功率比例为 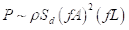 对于像Finbot这样的自推进水下机器人来说,从静止状态开始推进需要有限的能量,因为内部机械和电气效率低下会损失一些能量。因此,实际上,随着振荡频率接近零,输入功率接近一个大于零的常数,因此
对于像Finbot这样的自推进水下机器人来说,从静止状态开始推进需要有限的能量,因为内部机械和电气效率低下会损失一些能量。因此,实际上,随着振荡频率接近零,输入功率接近一个大于零的常数,因此
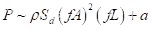 ,其中a (> 0)是常数。假设游泳模式具有恒定的拍打幅度和质量,那么CoT的比例为:
,其中a (> 0)是常数。假设游泳模式具有恒定的拍打幅度和质量,那么CoT的比例为:

等式(1)中的第一项随着速度的增加而增加,对于低速,st按
R
e
−
1
/
4
Re^{-1/4}
Re−1/4的比例增加,对于高速,St保持相对恒定,则为
U
2
U^2
U2。第二项与速度的倒数1/U成比例减小。等式(1)中的两项相加得到一个速度值,使得CoT最小。
3.结果
Finbot是第一个自主仿生多鳍平台,其体积足够小,可用于闭环控制下的三维仿鱼游泳实验研究。本节重点介绍了新设计的机器人的关键方面,随后是一系列实验,以探索不同尾鳍的性能,并演示鱼类的游泳。
3.1.Finbot的设计使多鳍自主自推进游泳
Finbot是自推进的,完全自主的,使用四个独立可控的鳍和来自IMU 和压力传感器的反馈进行水下自由游泳(见方法)。由于有四个鳍,Finbot具有很高的机动性,能够跟随大范围的指定轨迹,这支持了各种实验的设计。由于Finbot也很小,所以这种实验可以在用于鱼类实验室研究的相同流动池中进行,其中包括PIV在内的数据采集是最直接、可靠和有效的。Finbot(图1)的设计灵感来自对鱼类游泳的观察,其流线型外形的灵感来自蓝色唐(肝片吸虫)的测量身体尺寸。紧凑型车身由3D打印而成,分为两半,重160克,最长尺寸为122毫米,不包括尾鳍,我们将其定义为一个车身长度(BL)。
一个可替换的尾鳍,通过鳍和身体之间的磁性连接实现,使我们能够快速交换鳍,并在自由游泳实验中测试各种鳍的设计。所有的翅片都是从不同厚度和柔性的塑料垫片材料上激光切割下来的(Artus公司)。鳍状机器人的尾部设计包括一个单一的关节,被动和灵活的尾鳍通过这个关节连接到主体,因此最接近于thunniform游泳 [48] 。金枪鱼类游泳者专门用于高速游泳,并具有相对刚性的中央身体区域,用于肌肉动力装置,还提供惯性以避免大的反冲运动 [49] 。由于机械上的限制,鳍状肢的尾柄不如鳍状肢的尾柄尖。尾鳍在对称和机械约束极限之间绕中性轴自由旋转,正弦俯仰运动由尾鳍输入功率的调制规定。在所有驱动频率下,尾部拍击幅度保持不变,并调整至大约20%的体长(图1©),因为发现这一比例可最大限度地减少不同鱼类物种巡航游泳的能量消耗 [44] ;然而,具有不同振幅的致动器的连接是可能的。
我们将Finbot设计成易于复制和修改,使用现成的电子产品和3d打印材料。视频S1和附录的第1节给出了设计细节,我们之前的出版物 [30] 中描述了早期版本的鳍致动器。
3.2.Finbot的游泳性能与鱼类相似
遵循自然比例定律(见方法),许多鱼类表现出游泳速度和尾巴跳动频率之间的近似线性关系 [8,9] ,CoT 也呈U形曲线,在中速时具有最小值 [10–12] 。在模仿鱼类游泳时,Finbot也表现出了这些特征(图2)。Finbot的巡航速度范围为
36
m
m
s
−
1
36\ \rm mm\ s^{-1}
36 mm s−1至
122
m
m
s
−
1
122\ \rm mm\ s^{-1}
122 mm s−1 (=
B
L
s
−
1
\rm BL\ s^{-1}
BL s−1),当速度大于约
70
m
m
s
−
1
70\ \rm mm\ s^{-1}
70 mm s−1(层流和紊流之间的实验确定的边界,见图2(a))时,与频率成线性比例关系。斯特劳哈尔数遵循与各种鱼类相同的上凹曲线 [44,45] ,并在高速时稳定在0.95左右(图2(b))。此外,在紊流区的不同速度下,阻力系数
C
d
C_d
Cd大致保持不变,为0.06(补充图S4(B))。
对游泳的能量学分析表明,功率范围从0.97 W到3.3 W,并与频率的立方成比例(图2©),而随着f的降低,功率接近一个有限值(参见方法)。无量纲CoT在3 Hz左右的接近最佳的尾拍频率的狭窄范围内被最小化到大约15 (图2(d))。最后,Finbot实验的雷诺数范围从4438到14891(图2(b))。这是在小尺寸鱼的范围内,并且在层流和湍流状态之间的过渡 [45] 。因此,鳍状机器人身体的总阻力主要是形状阻力,而不是表面摩擦阻力 [11] 。阻力测量提供了对不同游泳速度下产生的推力的估计(补充图S4(A))。例如,以1
B
L
S
−
1
\rm BL\ S^{-1}
BL S−1的速度游泳时需要克服的阻力是8 mN。
3.3.鱼鳍在游泳性能
鉴于使用基线鳍进行鱼类游泳的初步结果,我们研究了不同的尾鳍,以确定能够提高速度和成本的形状和刚度,同时还表现出游泳鱼的反向卡门街尾迹特征。在第一轮测试中,我们分析了12个不同尺寸、厚度和形状的翅片的两个性能类别,即速度和成本(图3(a)至©)。此外,我们可视化了所有尾翼的尾涡结构(补充图S6)。
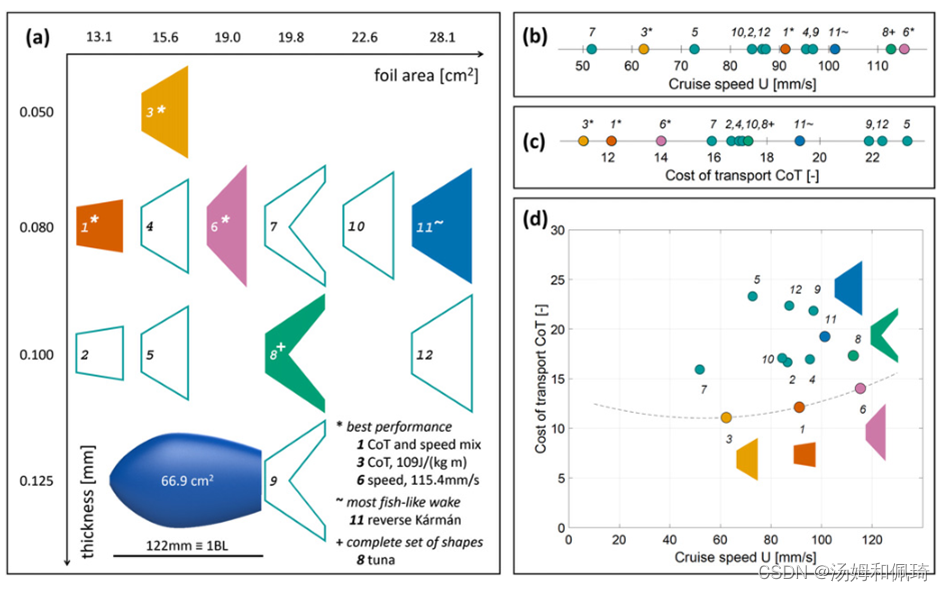
图3 12个不同翼片在2 Hz尾拍频率下的性能状况。(a)我们在Finbot(按比例绘制)上分析了12个不同尺寸、厚度和形状的鳍,所有这些鳍都以2 Hz的尾拍频率运行。机器人主体具有
66.9
c
m
2
66.9\ \rm cm^2
66.9 cm2 的平面表面积。五个鳍片(1,3,6,8,11)根据它们在( b )巡航速度和 ( c ) CoT中各自的性能被选择用于进一步研究。(d)与所有其他翅片相比,翅片1、3、6表现出优异的性能,使它们成为最优鳍组。鳍3比鳍1和6更灵活;鳍6比鳍1更大,更呈梯形。更灵活的鳍3显示出最小的成本,而更大的鳍6产生最高的速度。在鳍1、3、6中,CoT和速度是折衷的,并且可以根据期望的性能要求来选择afin。结果,这三个鳍形成了一个帕累托最优边界(拟合虚线,
C
o
T
∼
U
2
CoT \sim U^2
CoT∼U2)。(b)–(d):测量点是N = 3次试验的平均值μ。
寻找高性能的鳍是一个多目标优化,其中成本和速度是相关的(图3(d))。我们感兴趣的是寻找帕累托最优鳍,即只能在成本或速度方面改进的鳍,而不能同时在两方面改进。使用等式(1)中的成本比例定律,我们拟合了三个鳍1、3和6的帕累托最优边界,这三个鳍在速度或成本方面表现最佳(图3(d)中的虚线)。这个边界是近似和保守的,原因有二。首先,这三个鳍的设计大概接近最佳设计,但不是完全最佳,因此留有改进的余地。第二,用于所有对比试验的2 Hz的尾部拍频不一定能使U形CoT最小化。可能存在进一步优化CoT而不损害速度的频率。为了以帕累托最优方式操作,即在CoT和速度的增益相冲突的情况下,鳍必须在其U形CoT曲线的单调递增区域中运行。
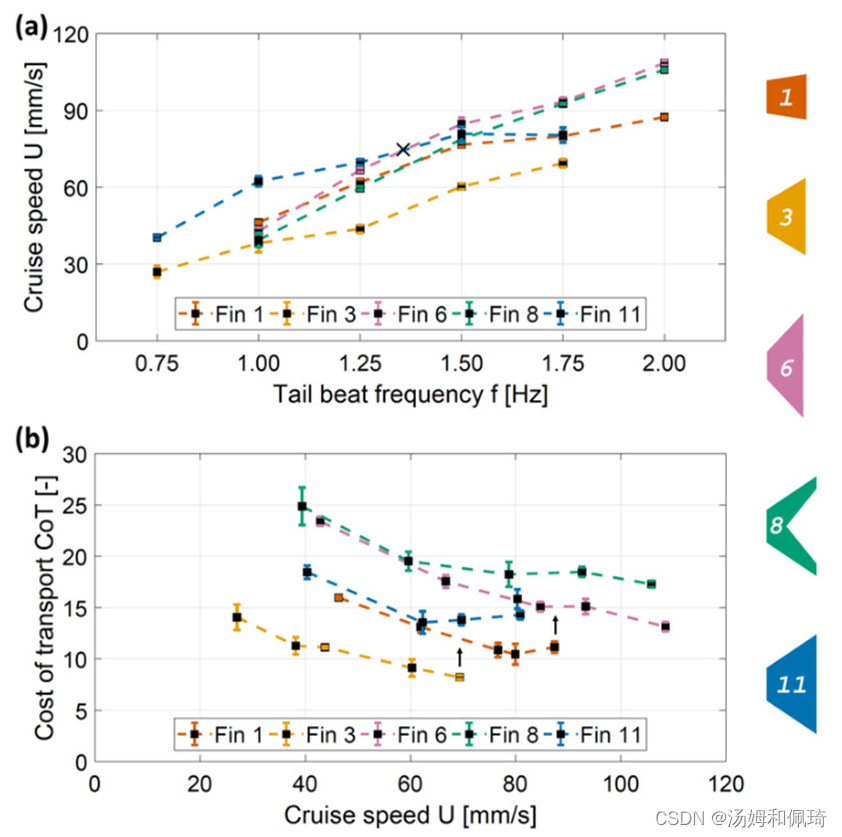
图4 五个选定fin的速度和成本频率扫描。不同的鳍分别在不同的尾拍频率和速度下实现各自的最佳性能——速度或CoT。(a)当fin 11低于1.25 Hz且fin 6高于1.5 Hz时达到最大速度(过渡用黑色十字标记)。(b)fin 3的速度低于
69
m
m
s
−
1
69\ \rm mm\ s^{-1}
69 mm s−1 ,fin 1的速度介于
69
m
m
s
−
1
69\ \rm mm\ s^{-1}
69 mm s−1 和
87
m
m
s
−
1
87\ \rm mm\ s^{-1}
87 mm s−1 之间,fin 6的速度高于
87
m
m
s
−
1
87\ \rm mm\ s^{-1}
87 mm s−1 时,CoT最小(过渡用黑色箭头标记)。(a)和(b):黑色方块是N = 3次试验的平均值μ。误差线描绘了平均值的标准偏差σ,其中一些被黑色方块遮住了。
由于在2 Hz时,没有一个鳍在速度、CoT和涡流结构中占主导地位,我们选择了五个不同的鳍(1、3、6、8、11)在多个频率上进行第二轮测试(图4): (i)矩形鳍1,在达到 91.2 m m s − 1 91.2\ \rm mm\ s^{-1} 91.2 mm s−1的高速时,CoT值为12.1;(ii)具有11.1的最低CoT的菱角属3;(三)最高速度为 115 m m s − 1 115\ \rm mm\ s^{-1} 115 mm s−1的梯形翼翼6;(iv)具有大多数鱼状涡旋结构的梯形鳍11;和(v)金枪鱼鳍8,以完成形状的混合[为了获得更好的性能,选择金枪鱼鳍7和9,见图3(b)-(d)]。当鳍6为2 Hz时,我们获得的最高速度为 109 m m s − 1 109\ \rm mm\ s^{-1} 109 mm s−1 (= 0.9 B L s − 1 0.9\ \rm BL\ s^{-1} 0.9 BL s−1 )(图4(a))。为了在所有频率下以最高速度运行,鳍11应选择1.25 Hz,鳍6从1.5 Hz开始。CoT分析(图4(b))证实了鳍1、3、6的性能优于鳍8和11。为了在最小CoT下运行,鳍3应在 69 m m s − 1 69\ \rm mm\ s^{-1} 69 mm s−1以下的低速下使用,鳍1在 69 m m s − 1 69\ \rm mm\ s^{-1} 69 mm s−1和 87 m m s − 1 87\ \rm mm\ s^{-1} 87 mm s−1之间的中速下使用,鳍6在 87 m m s − 1 87\ \rm mm\ s^{-1} 87 mm s−1以上的高速下使用。鳍3在 69 m m s − 1 69\ \rm mm\ s^{-1} 69 mm s−1的速度下获得了8.2的最低CoT。驱动频率的范围受到最大输入功率的限制,并取决于翅片的尺寸和厚度,因此在不同的翅片之间是不同的。
3.4.最小的运输成本和最明显的逆向卡门尾流是相互关联的。
鳍选择的另一个标准是类似鱼的旋涡脱落,其动机是将鳍状机器人建立为仿生平台。图5显示了五个选定尾翼(1,3,6,8,11)中每一个的两个尾流——一个在低尾拍频率和次优CoT下,另一个在中高频和改进CoT下。所有尾翼都表现出更强和更少分叉的尾流,趋向更优的CoTs。为了在U形曲线右端CoT增加的区域进行测试,我们在额外的实验中测试了高达4 Hz的频率(补充图S7)。在最小的CoTs和中等速度下,鳍6展示了它最有效和最像鱼的反卡门尾流。非常低或非常高的速度导致分叉的尾流结构,由于横向损失,这种结构的效率较低。

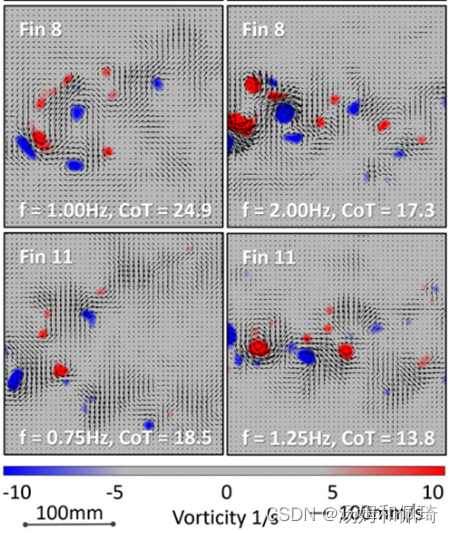
图5 最佳和接近最佳CoTs的尾流结构五个选定尾翼中的每一个分别在次优CoTs和低尾拍频率f(左栏)下,与接近最优CoTs和中到高尾拍频率和速度(右栏)相比,显示出不太明显或更分叉的尾流结构。
3.5. 鳍状机器人能像鱼一样游泳
我们使用蓝鳃太阳鱼(L. macrochirus)作为模式鱼种,从自由游动的鱼中获得尾流结构的比较数据。Finbot和bluegill以大约 1.3 B L s − 1 1.3\ \rm BL\ s^{-1} 1.3 BL s−1的相似典型速度游泳,并且具有可比较的身体轮廓,质量和长度分别约为138 g和195 mm [12] 。此外,在蓝鳃鲷体上测得的阻力与在鳍状机器人上测得的阻力相似 [50] 。图6显示了鳍11在2 Hz和蓝鳃鲷并排的情况下,鳍机器人后面的尾流实例。两者都表现出视觉上相似的反卡门街鱼类游泳的特征。这些反向卡门街道在所有实验中都是稳定的;也就是说,其它时刻的尾流看起来是相似的。虽然鳍11产生了最像鱼的尾流,但包括6、7、8、9、10在内的其他几个鳍也类似于鱼的游动(见图5和补充图S6和S7)。
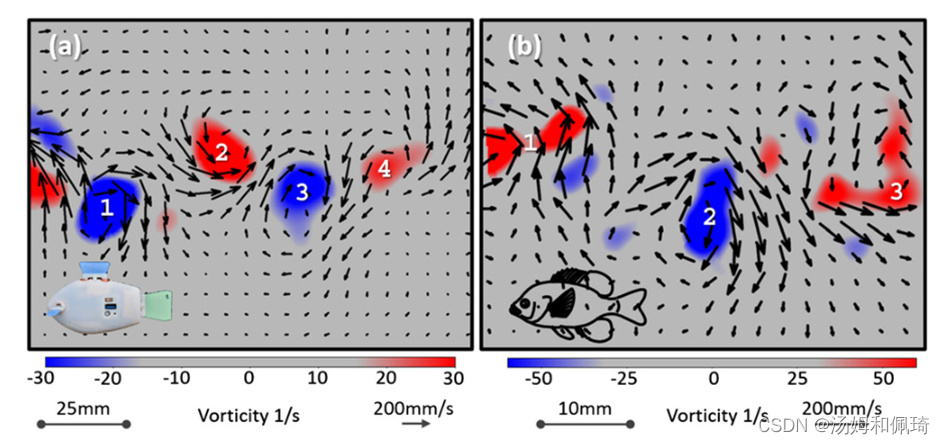
图6 鱼状尾迹。(A)一条反向的卡门街,这是鱼类跟随鳍状机器人游动的特征,用鳍11以
0.9
B
L
S
−
1
0.9\ BL\ S{-1}
0.9 BL S−1 和2 Hz的尾拍频率游动。(b)蓝鳃太阳鱼尾部的三个漩涡。(a)和(b):鳍尖在每个面板的左边缘,并且按比例缩小的鳍状鱼和蓝鳃太阳鱼分别显示在(a)和(b)的左下方。
4.本文主要贡献
设计和测试了一种具有仿生多鳍结构的仿鱼自主游泳机器人Finbot。我们的结果表明,通过选择尾鳍,鳍机器人可以实现鱼类特有的游泳行为,从而在不同的尾拍频率下产生反向卡门尾流和类似鱼类的速度和CoT性能。用粒子图像测速仪对尾流结构进行可视化,证明了类似鱼的反向卡门尾流,特别是在接近最佳CoTs时(图5)。正如在fish中观察到的,速度与尾拍频率成线性比例,CoT与速度的关系曲线呈U形(图2)。速度、功率和成本的实验数据所对应的函数(图2)与鱼类生物学研究中验证的基于物理学的预期比例关系相匹配 [8–12,44–47]。这些函数可用于估算未经测试的尾拍频率下的速度、功率和成本。
对最优鳍的搜索揭示了速度和成本之间的权衡(图3(d)),这解释了为什么在鱼类物种中可以发现如此多的鳍。与我们的机器人相反,鱼类对其尾鳍的刚度有主动控制 [51,52],允许它们在更快的速度下加强鳍以抵抗更高的流体动力载荷 [52] 。在实验室实验中证实了尾翼刚度的重要性及其对推进力的影响,因此尾翼拍频越高,尾翼的速度就越高 [16,53] 。我们的实验重现了这一趋势(图2–4)。最高速度(
122
m
m
s
−
1
=
1
B
L
s
−
1
122\ \rm mm\ s^{-1} = 1 \ \rm BL\ s^{-1}
122 mm s−1=1 BL s−1)和最低速度(CoT = 8.2)是通过两种不同的尾翼实现的(图2和图4)。除了控制过度僵硬,鱼可以在步态之间转换,以在各种速度下优化它们的婴儿床 [1,12] 。对于Finbot来说,通过简单地交换尾鳍,可以改变刚度和步态。这可以实现不同的目标,如使用鳍6以最高速度游泳,或使用鳍3以最小的成本将鳍机器人的范围最大化到1150米(图4)。此外,Finbot的设计提供了对超出我们在自然界中所见的变化的控制,从中可以产生更全面的性能景观。
速度和成本之间的权衡意味着当将机器人身体与尾鳍配对时,没有单一的最佳组合。除了优化鳍的形状、尺寸或刚度之外,这些参数必须与合适的驱动配对,即与鳍的“资产”匹配的振荡模式(频率和振幅)。当可视化五种不同尾翼的尾流结构时,我们发现理想的反向卡门尾流主要出现在最小CoTs处(图5)。因此,给定机器人身体和尾鳍,有两个设计标准可供选择,这两个标准都确保在接近最佳的CoT下有效运动:(i)通过测量功率和速度在最小的CoT下运行机器人;(ii)通过可视化机器人尾流(仅通过一项相关工作 [25] 实现),确认旋涡脱落导致反向卡门街。
据我们所知,Finbot是第一个也是最小的多鳍自主水下机器人,它也忠实地复制了鱼类游泳的多种特征。Finbot的速度与许多小型水下机器人相似 [20,21,27–29] 。很少有其他基于鱼的机器人设计报告功耗和成本。这两个设计示例(CoT为12.7的tunalike Tunabot和CoT为0.3的turtlelike Madeleine)很难与Finbot (CoT为8.2)进行详细比较,因为它们的驱动机制和尺寸差异很大。为了将Finbot的游泳性能与真鱼的游泳性能联系起来,我们选择了一条蓝鳃太阳鱼,因为它的身体轮廓相似 [12] 。Finbot的最大速度(
1
B
L
s
−
1
≡
122
m
m
s
−
1
1 \ \rm BL\ s^{-1}≡122\ \rm mm\ s^{-1}
1 BL s−1≡122 mm s−1)接近bluegill的典型速度(
1.3
B
L
s
−
1
≡
250
m
m
s
−
1
1.3 \ \rm BL\ s^{-1} ≡ 250\ \rm mm\ s^{-1}
1.3 BL s−1≡250 mm s−1)。然而,比较鳍足类的CoT(
8.2
≡
80.4
J
k
g
m
−
1
8.2≡ 80.4J\ kgm^{-1}
8.2≡80.4J kgm−1)和蓝鳃类的CoT(
0.25
≡
2.5
J
k
g
m
−
1
0.25≡ 2.5J\ kgm^{-1}
0.25≡2.5J kgm−1),我们注意到一个数量级的差异,表明与鱼类相比整体运动效率较低。观察2.1 mN[补充图S4(A)]的推力F,在
69
m
m
s
−
1
69 \ \rm mm\ s^{-1}
69 mm s−1的自由游泳速度下克服阻力所需的推力,对应于鳍状机器人的最小CoT(图4(b)),我们可以推导出在水中移动鳍状机器人形状和质量m的物体的成本的理论下限,
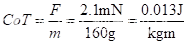 。这个理论上的下限,仅仅是由鳍状肢的形状和质量决定的,低于蓝鳃太阳鱼。因此,与realfish相比,我们将Finbot的高成本和低效运动与从电池电源产生前进速度的过程相关联,并假设在故意低效的电磁致动器中存在最大的转换损失(见补充第5节和 [30] )。相比之下,反向卡门尾流(图6)和低剖面阻力(补充图S2)是有效水上推进的线索。
。这个理论上的下限,仅仅是由鳍状肢的形状和质量决定的,低于蓝鳃太阳鱼。因此,与realfish相比,我们将Finbot的高成本和低效运动与从电池电源产生前进速度的过程相关联,并假设在故意低效的电磁致动器中存在最大的转换损失(见补充第5节和 [30] )。相比之下,反向卡门尾流(图6)和低剖面阻力(补充图S2)是有效水上推进的线索。
然而,Finbot的推进力可以通过重新设计尾部区域来改进,尾部区域目前受到电磁致动器的限制(图1(b))。尾柄横截面积的减少将使水流附着在身体和鳍上[补充图S5(B)],并有助于有效游泳 [5] 。有效的波动性鱼类游泳依次表现为0.2至0.4之间的受限Strouhal数 [4,52] 。虽然我们获得的鳍式机器人的最低Strouhal数——在1.5 Hz的尾拍频率和
87
m
m
s
−
1
87\ \rm mm\ s^{-1}
87 mm s−1 的速度下,鳍6的Strouhal数分别为0.53——接近上限,但速度慢的鱼移动通常会导致Strouhal数接近0.6 [55] 。鳍状机器人的斯特劳哈尔数随着游泳速度的增加而减少(图2(b)),与鱼类运动中观察到的情况类似 [5,55] 。
受鱼启发的机器人已经在海洋中运行 [20,21] ,我们对在实验室中游泳的机器鱼的持续研究可以有益于未来的开放水域设计。类鱼机器人系统以类似于自由游动的鱼的方式用多个鳍来控制它们的3D位置的能力将导致更有效的水下机器人,其结合了机动性和自主鱼类游动。这将促成新的尝试,如在珊瑚礁等高生态敏感性区域进行数据采样。Finbot平台也非常适合仿生鱼分析,因为它实现了闭环鱼般的游泳特性,其大小和可操作性适用于复杂和可重复的实验室实验。通过板载功耗测量,Finbot从一个新的角度打开了理解鱼类游泳的大门,并有助于完成对水生运动的更全面的看法,例如在鱼群等领域,我们设想用配备摄像头的finbot进行协调的多机器人实验。













![P1055 [NOIP2008 普及组] ISBN 号码————C++](https://img-blog.csdnimg.cn/e5f6f20a8f304e5e9f4cd1f5b801d6b8.png)
