一、题目

1、题目描述

在二维平面上的 x 轴上，放置着一些方块。

给你一个二维整数数组 positions ，其中 $positions[i]=[lef{t}_i,sideLengt{h}_i]$ 表示：第 i 个方块边长为 $sideLengt{h}_i$ ，其左侧边与 x 轴上坐标点 $lef{t}_i$ 对齐。

每个方块都从一个比目前所有的落地方块更高的高度掉落而下。方块沿 y 轴负方向下落，直到着陆到 另一个正方形的顶边 或者是 x 轴上 。一个方块仅仅是擦过另一个方块的左侧边或右侧边不算着陆。一旦着陆，它就会固定在原地，无法移动。

在每个方块掉落后，你必须记录目前所有已经落稳的 方块堆叠的最高高度 。

返回一个整数数组 ans ，其中 ans[i] 表示在第 i 块方块掉落后堆叠的最高高度。

示例1：

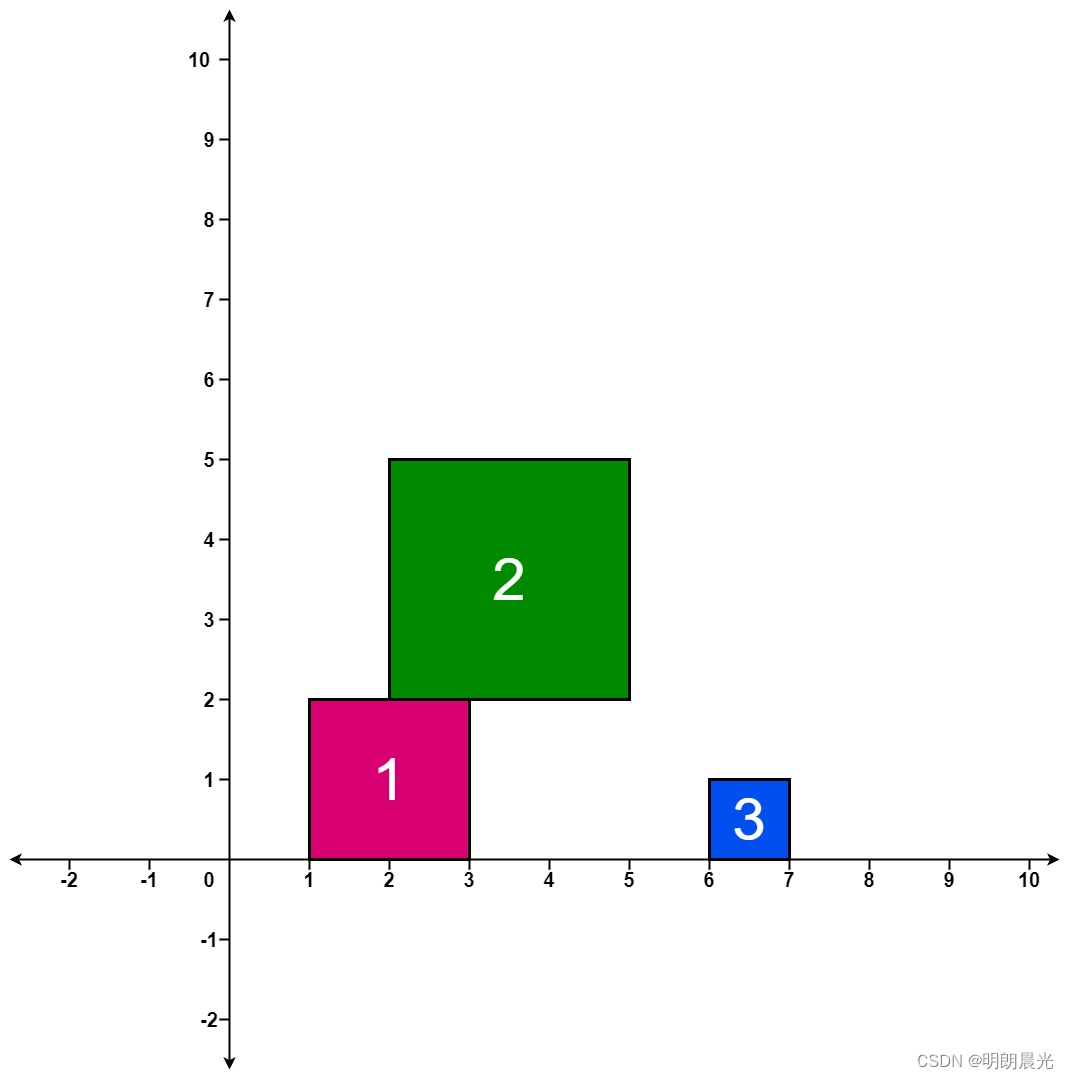
输入：positions = [[1,2],[2,3],[6,1]]
输出：[2,5,5]
解释：
第 1 个方块掉落后，最高的堆叠由方块 1 组成，堆叠的最高高度为 2 。
第 2 个方块掉落后，最高的堆叠由方块 1 和 2 组成，堆叠的最高高度为 5 。
第 3 个方块掉落后，最高的堆叠仍然由方块 1 和 2 组成，堆叠的最高高度为 5 。
因此，返回 [2, 5, 5] 作为答案。

示例2：

输入：positions = [[100,100],[200,100]]
输出：[100,100]
解释：
第 1 个方块掉落后，最高的堆叠由方块 1 组成，堆叠的最高高度为 100 。
第 2 个方块掉落后，最高的堆叠可以由方块 1 组成也可以由方块 2 组成，堆叠的最高高度为 100 。
因此，返回 [100, 100] 作为答案。
注意，方块 2 擦过方块 1 的右侧边，但不会算作在方块 1 上着陆。

2、基础框架

class Solution {
public:
    vector<int> fallingSquares(vector<vector<int>>& positions) {

    }
};

3、原题链接

699. 掉落的方块

二、解题报告

1、思路分析

利用线段树。
题目分析：比如第一个方块[1,2]，对应成线段树就是区间[1, 3) （靠着1，长度为2，所以能到达x轴的3位置，但是为了防止贴边，所以区间左闭右开）每个位置的值加2。

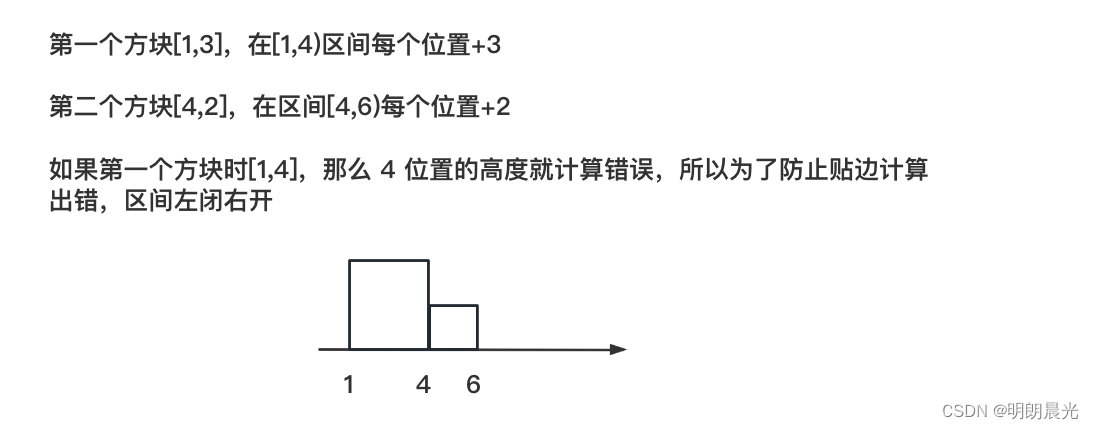
如果有一个新的方块落下来[left, sideLength]，要先查询 [left, left + sideLength) 这个范围上的最大高度值 maxH，就知道落到这个高度后不能往下再落了，将[left, left + sideLength]区间上的所有高度全部更新为 maxH + sideLength，这个区间上原先的值为多少不再关心。

整体而言，就是一个 更新 + 查询max的线段树

2、时间复杂度

$O(nlogn)$

3、代码详解

• C++

class Solution {
public:
    class SegmentTree {
    private:
        int *maxH;
        int *change;
        bool *updateMark;

    public:
        //线段树初始化
        SegmentTree(int size) { //x轴上的数开始都为0，不存在数组
            int n = size + 1;
            maxH = new int[n << 2]();
            change = new int[n << 2]();
            updateMark = new bool[n << 2]();
        }

    private:
        //根节点的最大值
        void pushUp(int rt) { 
            maxH[rt] = max(maxH[rt << 1], maxH[rt << 1 | 1]); //从左右子树中得到最大值
        }    

        //向下一级分发任务
        void pushDown(int rt, int ln, int rn) {
            if (updateMark[rt]) {
                updateMark[rt << 1] = true;
                updateMark[rt << 1 | 1] = true;
                change[rt << 1] = change[rt];
                change[rt << 1 | 1] = change[rt];
                maxH[rt << 1] = change[rt];
                maxH[rt << 1 | 1] = change[rt];
                updateMark[rt] = false;
            }
        }

    public:
        //更新
        void update(int L, int R, int C, int l, int r, int rt) {
            if (L <= l && r <= R) {
                change[rt] = C;
                updateMark[rt] = true;
                maxH[rt] = C;
                return ;
            }

            int mid = (l + r) >> 1;
            pushDown(rt, mid - l + 1, r - mid);
            if (L <= mid) {
                update(L, R, C, l, mid, rt << 1);
            }

            if (R > mid) {
                update(L, R, C, mid + 1, r, rt << 1 | 1);
            }

            pushUp(rt);
        }

        //查询
        int query(int L, int R, int l, int r, int rt) {
            if (L <= l && r <= R) {
                return maxH[rt];
            }
            int left = 0;
            int right = 0;
            int mid = (l + r) >> 1;
            pushDown(rt, mid - l + 1, r - mid);
            if (L <= mid) {
                left = query(L, R, l, mid, rt << 1);
            }

            if (R > mid) {
                right = query(L, R, mid + 1, r, rt << 1 | 1);
            }

            return max(left, right);
        }
    };

    unordered_map<int, int> index(vector<vector<int>>& positions) {
        set<int> pos;
        for (vector<int> &arr: positions) {
            pos.insert(arr[0]);
            pos.insert(arr[0] + arr[1] - 1);
        }

        unordered_map<int, int> _map;
        int count = 0;
        for (int index : pos) {
            _map[index] = ++count;
        }
        
        return _map;
    }

    vector<int> fallingSquares(vector<vector<int>>& positions) {
        unordered_map<int, int> _map = index(positions);
        int n = _map.size();

        SegmentTree *st = new SegmentTree(n);

        int maxH = 0;

        vector<int> res;
        for (vector<int> &arr : positions) {
            int L = _map[arr[0]];
            int R = _map[arr[0] + arr[1] - 1]; 
            int height = st->query(L, R, 1, n, 1) + arr[1]; 
            maxH = max(maxH, height);
            res.push_back(maxH);
            st->update(L, R, height, 1, n, 1);
        }
        return res;
    }
};

• Java

class Solution {
    public static class SegmentTree {
		private int[] max;
		private int[] change;
		private boolean[] update;

		public SegmentTree(int size) {
			int N = size + 1;
			max = new int[N << 2];

			change = new int[N << 2];
			update = new boolean[N << 2];
		}

		private void pushUp(int rt) {
			max[rt] = Math.max(max[rt << 1], max[rt << 1 | 1]);
		}

		// ln表示左子树元素结点个数，rn表示右子树结点个数
		private void pushDown(int rt, int ln, int rn) {
			if (update[rt]) {
				update[rt << 1] = true;
				update[rt << 1 | 1] = true;
				change[rt << 1] = change[rt];
				change[rt << 1 | 1] = change[rt];
				max[rt << 1] = change[rt];
				max[rt << 1 | 1] = change[rt];
				update[rt] = false;
			}
		}

		public void update(int L, int R, int C, int l, int r, int rt) {
			if (L <= l && r <= R) {
				update[rt] = true;
				change[rt] = C;
				max[rt] = C;
				return;
			}
			int mid = (l + r) >> 1;
			pushDown(rt, mid - l + 1, r - mid);
			if (L <= mid) {
				update(L, R, C, l, mid, rt << 1);
			}
			if (R > mid) {
				update(L, R, C, mid + 1, r, rt << 1 | 1);
			}
			pushUp(rt);
		}

		public int query(int L, int R, int l, int r, int rt) {
			if (L <= l && r <= R) {
				return max[rt];
			}
			int mid = (l + r) >> 1;
			pushDown(rt, mid - l + 1, r - mid);
			int left = 0;
			int right = 0;
			if (L <= mid) {
				left = query(L, R, l, mid, rt << 1);
			}
			if (R > mid) {
				right = query(L, R, mid + 1, r, rt << 1 | 1);
			}
			return Math.max(left, right);
		}

	}

    public HashMap<Integer, Integer> index(int[][] positions) {
		TreeSet<Integer> pos = new TreeSet<>();
		for (int[] arr : positions) {
			pos.add(arr[0]);
			pos.add(arr[0] + arr[1] - 1);
		}
		HashMap<Integer, Integer> map = new HashMap<>();
		int count = 0;
		for (Integer index : pos) {
			map.put(index, ++count);
		}
		return map;
	}

    public List<Integer> fallingSquares(int[][] positions) {
        HashMap<Integer, Integer> map = index(positions);
		int N = map.size();
		SegmentTree segmentTree = new SegmentTree(N);
		int max = 0;
		List<Integer> res = new ArrayList<>();
		// 每落一个正方形，收集一下，所有东西组成的图像，最高高度是什么
		for (int[] arr : positions) {
			int L = map.get(arr[0]);
			int R = map.get(arr[0] + arr[1] - 1);
			int height = segmentTree.query(L, R, 1, N, 1) + arr[1];
			max = Math.max(max, height);
			res.add(max);
			segmentTree.update(L, R, height, 1, N, 1);
		}
		return res;
    }
}