子矩阵的和
- 1.题目
- 2.基本思想
- 3.代码实现
1.题目
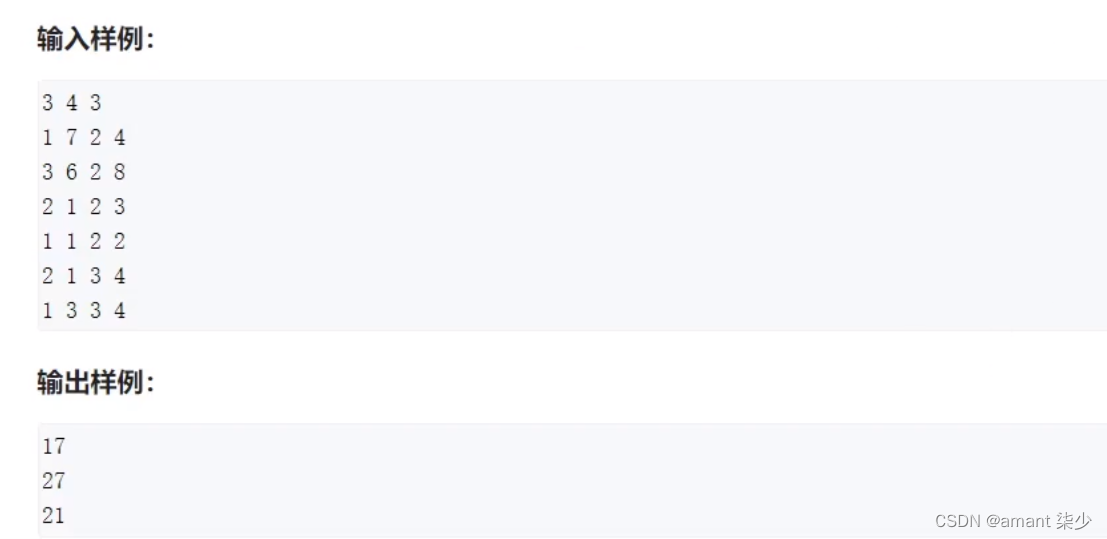
输入一个n行m列的整数矩阵,再输入q个询问,每个询问包含四个整数×1,y1,×2,y2,表示一个子矩阵的左上角坐标和右下角坐标。
对于每个询问输出子矩阵中所有数的和。
输入格式
第一行包含三个整数n,m,q。
接下来n行,每行包含m个整数,表示整数矩阵。
接下来q行,每行包含四个整数×1,y1,×2,y2,表示一组询问。
输出格式
共q行,每行输出一个询问的结果。
数据范围
1
≤
n
,
m
≤
1000
,
1≤n,m≤1000,
1≤n,m≤1000,
1
≤
q
≤
200000
,
1≤q≤200000,
1≤q≤200000,
1
≤
x
1
≤
x
2
≤
n
,
1≤x1≤x2≤n,
1≤x1≤x2≤n,
1
≤
y
1
≤
y
2
≤
m
,
1≤y1≤y2≤m,
1≤y1≤y2≤m,
一
1000
≤
矩阵内元素的值
≤
1000
一1000≤矩阵内元素的值≤1000
一1000≤矩阵内元素的值≤1000
2.基本思想
二维前缀和
容斥原理 容斥原理 容斥原理
1.
S
[
i
,
j
]
即为图
1
红框中所有数的的和为:
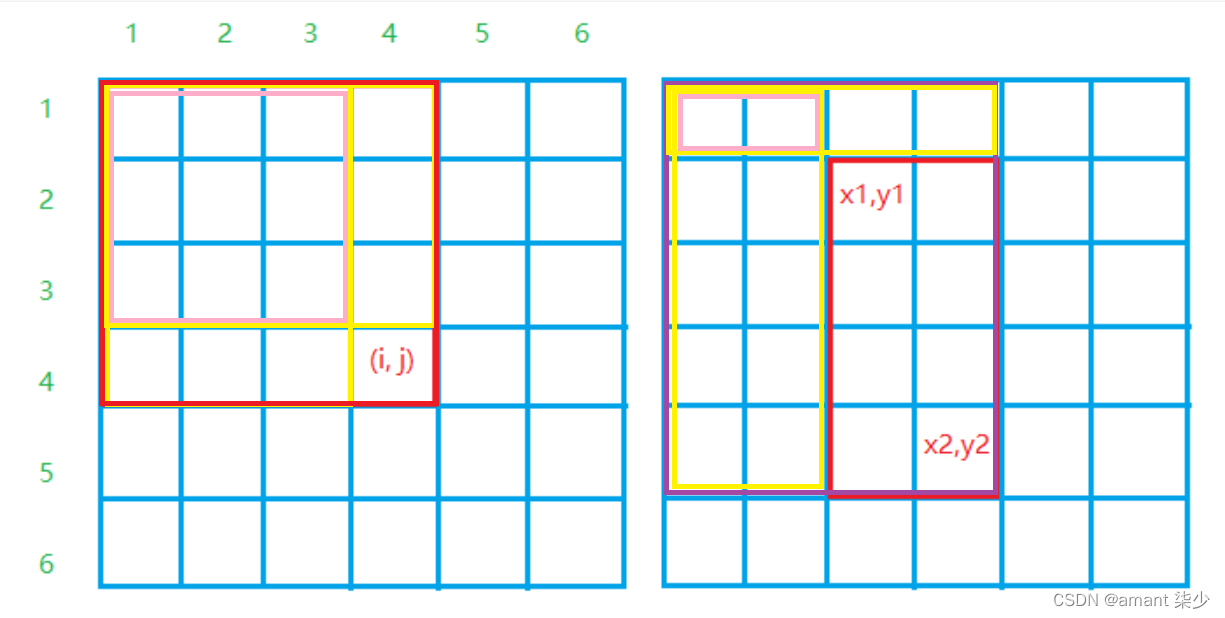
1.S[i,j]即为图1红框中所有数的的和为:
1.S[i,j]即为图1红框中所有数的的和为:
S
[
i
,
j
]
=
S
[
i
,
j
−
1
]
+
S
[
i
−
1
,
j
]
−
S
[
i
−
1
,
j
−
1
]
+
a
[
i
,
j
]
S[i,j]=S[i,j−1]+S[i−1,j]−S[i−1,j−1]+a[i,j]
S[i,j]=S[i,j−1]+S[i−1,j]−S[i−1,j−1]+a[i,j] 二维前缀和矩阵
2.
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
这一子矩阵中的所有数之和为:
2.(x1,y1),(x2,y2)(x1,y1),(x2,y2)这一子矩阵中的所有数之和为:
2.(x1,y1),(x2,y2)(x1,y1),(x2,y2)这一子矩阵中的所有数之和为:
S
[
x
2
,
y
2
]
−
S
[
x
1
−
1
,
y
2
]
−
S
[
x
2
,
y
1
−
1
]
+
S
[
x
1
−
1
,
y
1
−
1
]
S[x2,y2]−S[x1−1,y2]−S[x2,y1−1]+S[x1−1,y1−1]
S[x2,y2]−S[x1−1,y2]−S[x2,y1−1]+S[x1−1,y1−1]子矩阵
3.代码实现
import java.util.*;
public class Main{
private static int n, m, q;
private static final int N =1010;
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
n = in.nextInt();
m = in.nextInt();
q = in.nextInt();
int[][] a = new int[N][N];
int[][] s = new int[N][N];
// 输入数组初始化
for(int i = 1; i<=n; i++){
for (int j = 1; j <=m ; j++) {
a[i][j] = in.nextInt();
}
}
// 前缀和初始化
for (int i = 1; i <=n ; i++) {
for (int j = 1; j <=m ; j++) {
s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + a[i][j];//容斥原理
}
}
while (q-- >0) {
int x1 = in.nextInt();
int y1 = in.nextInt();
int x2 = in.nextInt();
int y2 = in.nextInt();
System.out.println(s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]);//容斥原理
}
}
}