目录
- 1. 题目描述
- 2. 一般思路
- 2.1 有问题的思路
- 2.2 全面但不高效的思路
- 2.3 面试小提示
- 3. 全面又高效的思路
1. 题目描述
- 题目:实现函数 double Power(double base,int exponent),求base 的exponent 次方。不得使用库函数,同时不需要考虑大数问题
2. 一般思路
2.1 有问题的思路
- 由于不需要考虑大数问题,这道题看起来很简单,可能不少应聘者在看到题目30秒后就能写出如下的代码:
#include <stdio.h>
float Power(double base, int exponent)
{
double result = 1.0;
for (int i = 0; i < exponent; i++)
{
result *= base;
}
return result;
}
int main()
{
double base = 0;
int exponent = 0;
scanf("%lf %d", &base, &exponent);
printf("%lf", Power(base, exponent));
return 0;
}
- 运行结果为:
- 不过遗憾的是,写得快不一定就能得到面试官的青睐,
- 因为面试官会问要是输入的指数(exponent)小于1
- 即是零和负数的时候怎么办?上面的代码完全没有考虑,只包括了指数是正数的情况。
2.2 全面但不高效的思路
- 我们知道当指数为负数的时候,可以先对指数求绝对值,然后算出次方的结果之后再取倒数。
- 既然有求倒数,我们很自然就要想到有没有可能对0求倒数,如果对0求倒数怎么办?
- 当底数(base)是零且指数是负数的时候,如果不做特殊处理,就会出现对0求倒数从而导致程序运行出错。怎么告诉函数的调用者出现了这种错误?
- 前面提到我们可以采用3种方法返回值、全局代码和异常。
- 面试的时候可以向面试官阐述每种方法的优缺点,然后一起讨论决定选用哪种方式。
- 最后需要指出的是,由于0的0次方在数学上是没有意义的,因此无论是输出0还是1都是可以接受的,
- 但这都需要和面试官说清楚,表明我们已经考虑到这个边界值了。
- 有了这些相对而言已经全面很多的考虑,我们就可以把最初的代码修改如下:
#define wucha 0.00000001
#include <stdio.h>
#include <math.h>
float Power(double base, int exponent)
{
if (abs(base) < wucha)
{
return 0.0;
}//底数为0,(底数指数都为0则结果默认为0)
if (exponent == 0)
{
return 1.0;
}//指数为0
double result = 1.0;
if (exponent > 0)
{
for (int i = 0; i < exponent; i++)
{
result *= base;
}
return result;
}//指数为正
else if (exponent < 0)
{
for (int i = 0; i > exponent; i--)
{
result *= base;
}
return 1 / result;
}//指数为负
}
int main()
{
double base = 0;
int exponent = 0;
while (scanf("%lf %d", &base, &exponent) != EOF)
{
printf("%lf\n", Power(base, exponent));
}
return 0;
}
- 运行结果为:
- 一个细节值得我们注意:在判断底数base是不是等于0时,不能直接写base=-0,
- 这是因为在计算机内表示小数时(包括 foat和 double 型小数)都有误差。判断两个小数是否相等,只能判断它们之差的绝对值是不是在一个很小的范围内。
- 如果两个数相差很小,就可以认为它们相等。
2.3 面试小提示
- 由于计算机表示小数(包括 foat和 double 型小数)都有误差,我们不能直接用等号(==)判断两个小数是否相等。如果两个小数的差的绝对值很小,比如小于 0.0000001,就可以认为它们相等。
3. 全面又高效的思路
- 此时我们考虑得已经很周详了,已经能够达到很多面试官的要求了。
- 但是如果我们碰到的面试官是一个在效率上追求完美的人,那么他有可能会提醒我们函数 Power还有更快的办法。
- 如果输入的指数 exponent为32,我们在函数 Power的循环中需要做 31次乘法。
- 但我们可以换一种思路考虑:我们的目标是求出一个数字的 32次方,如果我们已经知道了它的16次方,那么只要在 16 次方的基础上再平方一次就可以了。而16次方是8次方的平方。
- 这样以此类推,我们求32次方只需要做5次乘法:先求平方,在平方的基础上求4次方,在4次方的基础上求8次方,在8次方的基础上求16次方,最后在16次方的基础上求32次方。
- 也就是说,我们可以用如下公式求a的n次方:
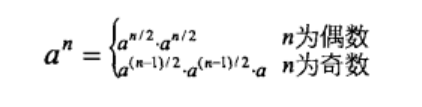
- 代码如下:
#include <stdio.h>
float Power2(double base, unsigned int exponent)
{
if (exponent == 0)
{
return 1;
}
if (exponent == 1)
{
return base;
}
double result = Power2(base, exponent >> 1);
result *= result;
if (exponent & 1 == 1)
{
result *= result;
}
return result;
}
int main()
{
double base = 0;
unsigned int exponent = 0;
while (scanf("%lf %d", &base, &exponent) != EOF)
{
printf("%lf\n", Power2(base, exponent));
}
return 0;
}
- 但是美中不足的是这个代码只能求非负数的非负数幂
最后,
恭喜你又遥遥领先了别人!











![[嵌入式AI从0开始到入土]14_orangepi_aipro小修补含yolov7多线程案例](https://img-blog.csdnimg.cn/direct/00a836bc433e442eaada08111db866cd.png)