目录
- 引言
- 一、蜗牛
引言
今天时间有点紧,只搞了一道题目,不过确实搞了三个小时,才搞完,主要是也有点晚了,也好累啊,不过也还是可以的,学了状态DP,把建图和spfa算法熟悉了一下,明天再接再厉。
一、蜗牛
标签:状态机DP
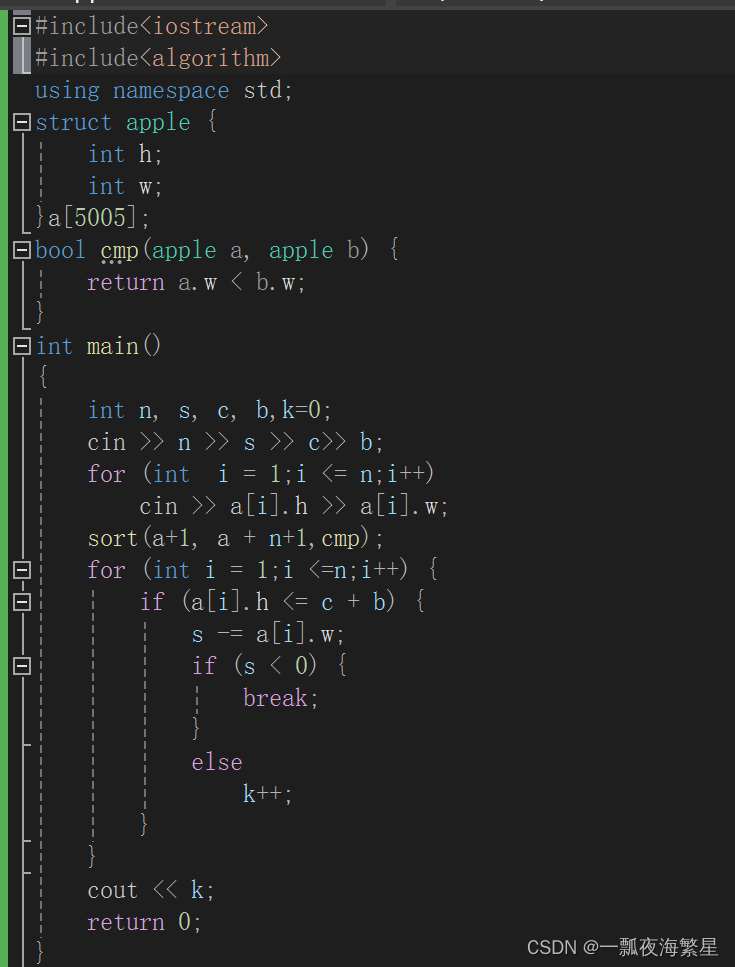
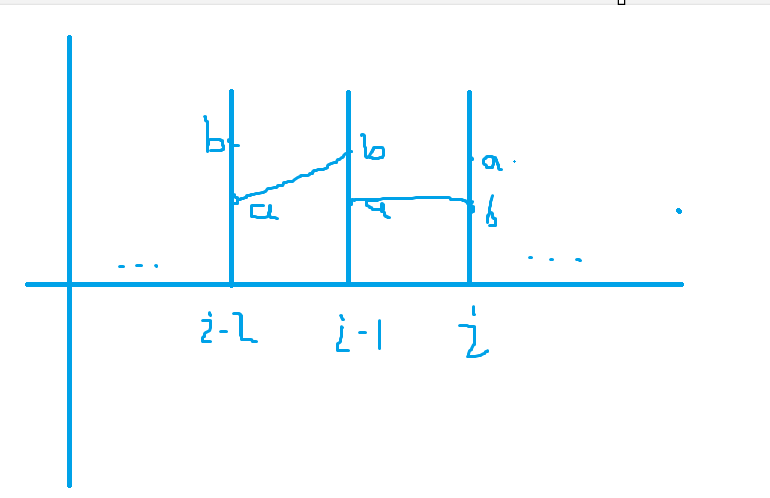
思路1:这个因为还没学所以第一时间没有这个DP的概念就拿最短路做的,spfa算法过了两个数据(总共十个),然后其实没问题,就是图建的不太完善,建图是觉得每次传送结束都要回到x轴,现在觉得可以继续走当前杆的下一个传送门再传送到下一个杆,因为每两个之间都有传送门,所以每根杆最多有两个传送门
思路2:直接用状态机DP,定义为两个状态f[i][2],分别代表第一次到达杆子的底端和b[i],然后结果就是两种情况:min(f[n][0],f[n][1]+b[n]/1.3),然后每次推f[i][0]、f[i][1]
i
n
t
d
=
x
[
i
]
−
x
[
i
−
1
]
;
int\ d = x[i] - x[i-1];
int d=x[i]−x[i−1];
f
[
i
]
[
0
]
=
m
i
n
(
f
[
i
−
1
]
[
0
]
+
d
,
f
[
i
−
1
]
[
1
]
+
g
e
t
(
b
[
i
−
1
]
,
0
)
+
d
)
;
f[i][0] = min(f[i-1][0] + d, f[i-1][1] + get(b[i-1], 0) + d);
f[i][0]=min(f[i−1][0]+d,f[i−1][1]+get(b[i−1],0)+d);
f
[
i
]
[
1
]
=
m
i
n
(
f
[
i
−
1
]
[
0
]
+
g
e
t
(
0
,
a
[
i
−
1
]
)
,
f
[
i
−
1
]
[
1
]
+
g
e
t
(
b
[
i
−
1
]
,
a
[
i
−
1
]
)
)
;
f[i][1] = min(f[i-1][0] + get(0, a[i-1]), f[i-1][1] + get(b[i-1], a[i-1]));
f[i][1]=min(f[i−1][0]+get(0,a[i−1]),f[i−1][1]+get(b[i−1],a[i−1]));
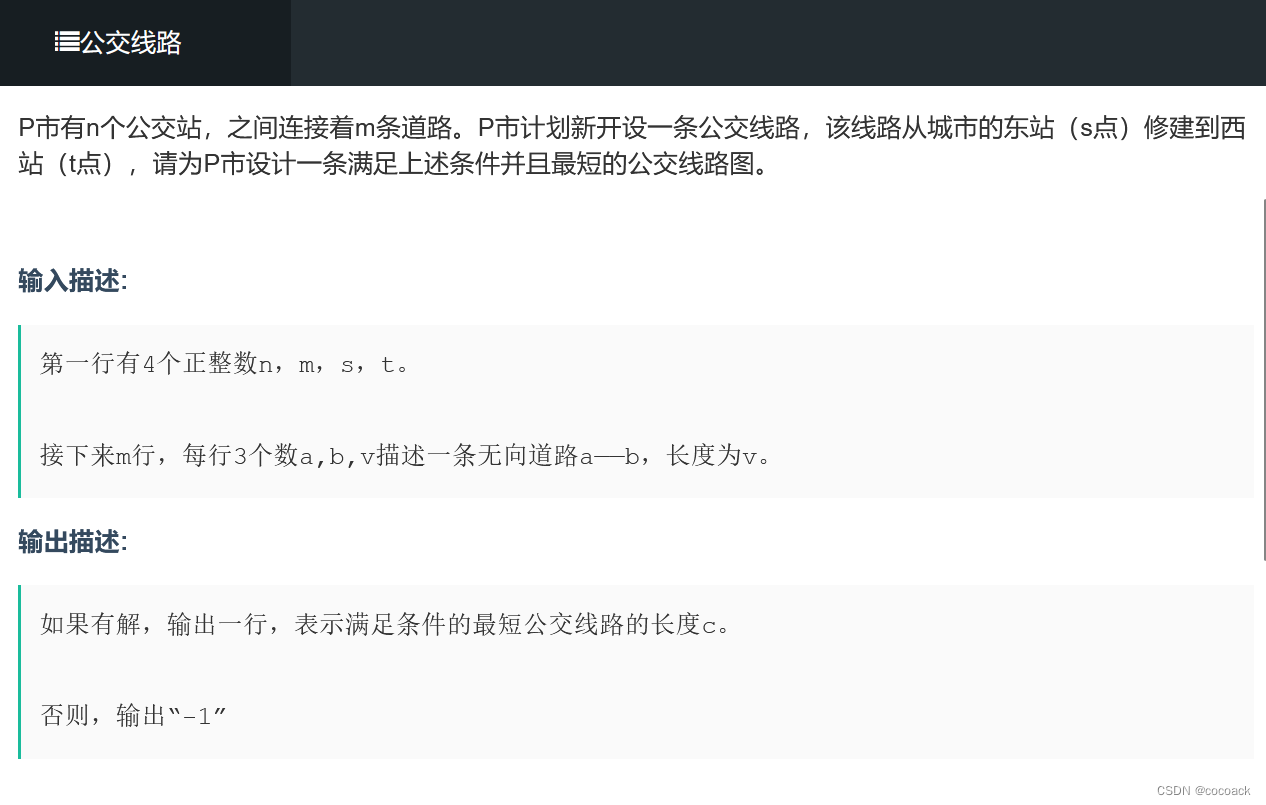
题目描述:
示例代码一:spfa算法(过了2/10)
#include <cstdio>
#include <cstring>
#include <iostream>
#include <vector>
#include <cfloat>
using namespace std;
const int N = 1e5+10, M = N * 2;
int n;
int h[N], e[M], ne[M], idx;
double w[M];
double dist[N];
bool st[N];
int q[N];
void add(int a, int b, double c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
double spfa()
{
for(int i = 0; i < N; ++i) dist[i] = DBL_MAX;
dist[0] = 0;
st[0] = true;
int hh = 0, tt = -1;
q[++tt] = 0;
while(hh <= tt)
{
auto t = q[hh++];
st[t] = false;
for(int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if(dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
if(!st[j])
{
q[++tt] = j;
st[j] = true;
}
}
}
}
return dist[n];
}
int main()
{
memset(h, -1, sizeof h);
scanf("%d", &n);
int a = 0, b;
vector<int> path;
for(int i = 0; i < n; ++i)
{
scanf("%d", &b);
path.push_back(b);
int c = b - a;
add(a,b,c);
a = b;
}
for(int i = 1; i < path.size(); ++i)
{
int a = path[i-1], b = path[i];
int t1, t2;
scanf("%d%d", &t1, &t2);
double c = t1 / 0.7 + t2 / 1.3;
add(a,b,c);
}
n = path.back();
double res = spfa();
printf("%.2f\n", res);
return 0;
}
示例代码二:状态机DP
#include <cstdio>
#include <iostream>
using namespace std;
const int N = 1e5+10, INF = 2e9;
int n;
int x[N], a[N], b[N];
double f[N][2];
double get(double x1, double x2)
{
if(x1 > x2) return (x1 - x2) / 1.3;
return (x2 - x1) / 0.7;
}
int main()
{
scanf("%d", &n);
for(int i = 1; i <= n; ++i) scanf("%d", &x[i]);
for(int i = 1; i < n; ++i) scanf("%d%d", &a[i], &b[i+1]);
for(int i = 0; i < n; ++i) f[i][0] = f[i][1] = INF;
f[1][0] = x[1];
for(int i = 2; i <= n; ++i)
{
int d = x[i] - x[i-1];
f[i][0] = min(f[i-1][0] + d, f[i-1][1] + get(b[i-1], 0) + d);
f[i][1] = min(f[i-1][0] + get(0, a[i-1]), f[i-1][1] + get(b[i-1], a[i-1]));
}
printf("%.2f\n", min(f[n][0], f[n][1] + get(b[n], 0) ) );
return 0;
}
![[嵌入式AI从0开始到入土]14_orangepi_aipro小修补含yolov7多线程案例](https://img-blog.csdnimg.cn/direct/00a836bc433e442eaada08111db866cd.png)


![[BIZ] - 1.金融交易系统特点](https://img-blog.csdnimg.cn/direct/6489c57a78dd4a3986cb1269c4e6dd2e.png)


![[职场] 投资顾问是做什么? #知识分享#其他#微信](https://img-blog.csdnimg.cn/img_convert/a818181f73740cbe5876cf253ddfa21e.png)