目录
先分个类吧:
1.对于有向无环图,我们直接拓扑排序,和AOE网类似,把取max改成min即可。
2.边权全部相等,直接BFS即可
3.单源点最短路
从一个点出发,到达其他顶点的最短路长度。
Dijkstra算法:用于一个节点到所有其他节点的最短路。(要求:不存在负权边,可以用于无向图)
先分个类吧:
1.对于有向无环图,我们直接拓扑排序,和AOE网类似,把取max改成min即可。
2.边权全部相等,直接BFS即可
3.单源点最短路
从一个点出发,到达其他顶点的最短路长度。

基本操作:松弛:d[u]+w<d[v],于是距离更改。
Dijkstra算法:用于一个节点到所有其他节点的最短路。(要求:不存在负权边,可以用于无向图)
具体过程:
1.开始之前,认为所有点都未计算,dis[]全部赋为极大值。
2.源点的dis[]=0;
3。计算与源点相邻的所有点的dis=map[s][v];
4.在还未算出最短路点的dis中选出最小一个点u,显然,因为不存在负权边,它的最短路就是dis.
5.对于与u相连的所有点v若dis[u]+map[u][v]比当前的dis小就松弛更新。
6.重复上述4,5操作。
正确性证明:
其实就是每一次贪心,显然,从源点开始的第一步得到的最短的路肯定就是最短路(到它的其他路肯定比它长)。
当我们把除源点外第一个确定的加入后,我们再用它去更新一下它连的点。
然后,我们选其中最小的点,它就是确定的。因为,要走到它,要么从那些没有确定最小路的点出发到它(因为这点是最小的点+无负权边,因此这样的点距离肯定更大),要么从已经确定的点上拓展出来,又因为他们不断地更新松弛(每一个确定最小路的点加入后,我们再用它去更新一下它连的点),所以我们可以保证在已经确定地点到最小的点的路径是最优的。因此,我们保证最小的点它就是确定的。
下面放一道模板题:
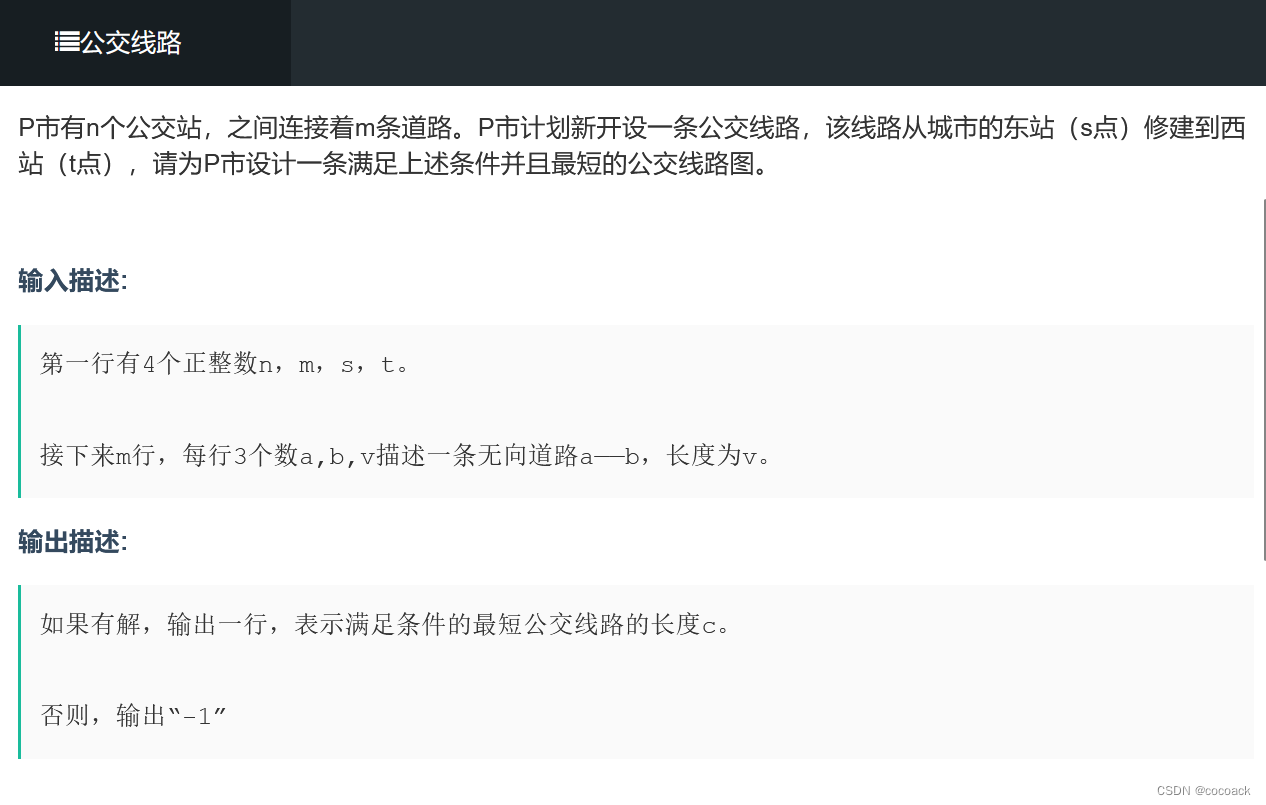
下面是AC代码(注意,无向边建图edge要2倍):
#include<bits/stdc++.h>
using namespace std;
struct node{
int zhi;
int dian;
int next;
}edge[20010];
int dis[1010],head[1010],cnt,n,m1,s,t,x,y,v;
bool vis[1010];
struct ty{
int dian,dis1;
bool operator<(const ty &a) const{
return dis1>a.dis1;
}
};
void merge(int x,int y,int v){
edge[++cnt].zhi=v;
edge[cnt].dian=y;
edge[cnt].next=head[x];
head[x]=cnt;
}
priority_queue<ty> q;
int dij(int s,int t){
q.push({s,0});
while(!q.empty()){
ty ck=q.top();
q.pop();
if(vis[ck.dian]==1) continue;
vis[ck.dian]=1;
for(int i=head[ck.dian];i!=-1;i=edge[i].next){
int i1=edge[i].dian;
if(vis[i1]==1) continue;
if(dis[i1]>dis[ck.dian]+edge[i].zhi){
dis[i1]=dis[ck.dian]+edge[i].zhi;
q.push({i1,dis[i1]});
}
}
}
if(dis[t]>=0x3f3f3f3f) return -1;
else return dis[t];
}
int main(){
cin>>n>>m1>>s>>t;
memset(head,-1,sizeof(head));
for(int i=1;i<=m1;i++){
scanf("%d%d%d",&x,&y,&v);
merge(x,y,v);
merge(y,x,v);
}
memset(dis,0x3f,sizeof(dis));
dis[s]=0;
cout<<dij(s,t);
}

![[BIZ] - 1.金融交易系统特点](https://img-blog.csdnimg.cn/direct/6489c57a78dd4a3986cb1269c4e6dd2e.png)


![[职场] 投资顾问是做什么? #知识分享#其他#微信](https://img-blog.csdnimg.cn/img_convert/a818181f73740cbe5876cf253ddfa21e.png)