介绍独立过程和独立增量过程。重点介绍两种独立增量过程-—维纳过程和泊松过程。
目录
前言
一、独立过程和独立增量过程
1、独立过程(Independent Process)
2、独立增量过程(Independent Increment Process)
二、正态过程(高斯过程)
1、正态过程的定义
编辑
2、正态过程的概率分布
三、维纳过程(Brown运动)
1、定义
2、概率分布及数学特征
3、性质
四、泊松过程
1、定义
2、概率分布及数字特征编辑
3、性质
4、更新计数过程
五、非齐次泊松过程
六、复合泊松过程
总结
前言
独立过程和独立增量过程在概率论和随机过程理论中有着重要的意义,它们提供了对随机现象和随机变量演变的一种数学描述,并在多个领域中有广泛的应用。
一、独立过程和独立增量过程
"独立过程"和"独立增量过程"是概率论和随机过程领域中的两个重要概念。
1、独立过程(Independent Process)
- 独立过程是指在一个时间或空间范围内,过程的不同部分之间是相互独立的。
- 对于一个时间序列来说,如果过程在不同时刻的取值是相互独立的,那么这个过程被称为是独立的。
- 例如,如果你投掷一枚骰子多次,每次投掷的结果是独立的,因为每次投掷的结果不受之前的投掷结果的影响。
独立过程的定义: 一个随机过程 {X(t), t ∈ T} 被称为是独立过程,如果对于任意不同的时间点 t₁, t₂, ..., tₙ,相应的随机变量 X(t₁), X(t₂), ..., X(tₙ) 都是相互独立的,即对于任意事件 A₁, A₂, ..., Aₙ,有:

这表示过程在不同时间点的取值是彼此独立的。

2、独立增量过程(Independent Increment Process)
- 独立增量过程是一种随机过程,其在不同时间间隔内的增量是相互独立的。
- 数学上,一个过程 {X(t), t ≥ 0} 被称为是独立增量过程,如果对于任意的 t1 < t2 < ... < tn,随机变量 X(t2) - X(t1),X(t3) - X(t2),...,X(tn) - X(tn-1) 是相互独立的。
- 常见的例子是布朗运动(Brownian Motion),其中在不同时间间隔内的位移是独立的。
总的来说,独立过程是指整个过程在不同的时间或空间点上是独立的,而独立增量过程则更具体地强调在不同时间间隔内的增量是独立的性质。
独立增量过程的定义: 一个随机过程 {X(t), t ≥ 0} 被称为是独立增量过程,如果对于任意正数 s < t 和任意正整数 n,增量 X(t) - X(s) 与 X(s), X(t) - X(t-1), X(t-1) - X(t-2), ..., X(tₙ) - X(tₙ-1) 都是相互独立的,即:
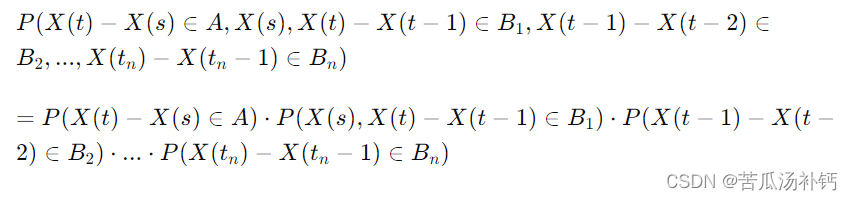
其中 A, B₁, B₂, ..., Bₙ 是任意事件。
这表示在不同时间间隔内的增量与过程在这些时间点的取值都是相互独立的。
平稳独立增量过程的定义:
一个随机过程 {X(t), t ≥ 0} 被称为是平稳独立增量过程,如果它同时满足以下两个性质:
平稳性(Stationarity): 对于任意正数 s < t 和任意正整数 n,随机变量 X(t)−X(s) 和 X(t−1)−X(t−2),..., X(t−n)−X(t−n−1) 具有相同的分布,即:

独立增量性(Independent Increment): 对于任意正数 s < t,增量 X(t)−X(s) 与过程在时间点 s 之前的取值X(s),以及X(t)−X(t−1) 与过程在时间点t−1 之前的取值 X(t−1) 都是相互独立的。

二、正态过程(高斯过程)
1、正态过程的定义
正态过程,也被称为高斯过程(Gaussian Process),是一类随机过程,其中任何有限个随机变量的线性组合仍然是正态分布的。换句话说,对于任意有限个时间点 {t₁, t₂, ..., tₙ},随机变量组 X(t1),X(t2),...,X(tn) 的线性组合(即 ∑i=1naiX(ti),其中 ai 是常数)的分布都是正态分布。
正态过程通常用来描述随机函数,其中每一个时间点的取值都是一个随机变量,而整个过程的取值随时间的推移形成一个随机函数。
具体来说,一个正态过程可以由均值函数(mean function)和协方差函数(covariance function)完全描述。对于所有的时间点 t₁ 和 t₂,均值函数给出了 E[X(t1)] 和 E[X(t2)] 之间的关系,而协方差函数则描述了X(t1) 和 X(t2) 之间的关联程度。
正态过程的性质使得它在贝叶斯统计、机器学习、回归分析等领域中得到广泛应用。在这些应用中,正态过程常常用来建模未知的随机函数,并通过观测数据对这些函数进行推断。其中,高斯过程回归(Gaussian Process Regression)是一个常见的应用示例。

2、正态过程的概率分布
正态过程(高斯过程)的概率分布是由均值函数(mean function)和协方差函数(covariance function)所决定的。用数学符号来表达:
考虑一个正态过程 {X(t), t ∈ T},其中 T 是时间的索引集合。对于任意有限个时间点 t₁, t₂, ..., tₙ,定义随机变量组 X(t1),X(t2),...,X(tn) 的联合概率分布为一个多维正态分布(高斯分布)。该多维正态分布的均值向量和协方差矩阵由均值函数 m(t) 和协方差函数k(t,s) 决定。
-
均值函数: m(t)=E[X(t)] 表示在时间点 t 处的均值。
-
协方差函数: k(t,s)=Cov(X(t),X(s)) 表示在时间点 t 和 s 处的协方差。
对于给定的时间点组合 t₁, t₂, ..., tₙ,多维正态分布的概率密度函数为:
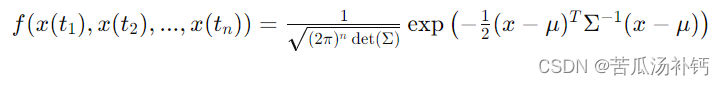
其中:
- x=[x(t1),x(t2),...,x(tn)] 是随机变量组成的列向量。
- μ=[m(t1),m(t2),...,m(tn)] 是均值向量。
- ΣΣ 是协方差矩阵,其元素为k(ti,tj)。
这个概率分布的关键特征是,对于任意有限个时间点,随机变量的线性组合仍然服从正态分布。这使得高斯过程在概率论、统计学和机器学习等领域中具有广泛的应用。
一维概率分布:

二维概率分布:

n维概率分布:

三、维纳过程(Brown运动)
维纳过程,也称为布朗运动(Brownian Motion),是一种经典的连续时间随机过程,最早由英国生物学家罗伯特·布朗(Robert Brown)在1827年观察到的。布朗运动在数学、物理学、金融学等领域都有广泛的应用和研究。
布朗运动的特征包括:
-
随机性: 布朗运动的路径是不连续的,并且在任意时间点的增量都是随机的,因此它是一种随机过程。
-
连续性: 布朗运动在时间上是连续的,即它的路径在任意时间点都是连续的。
-
马尔可夫性: 布朗运动具有马尔可夫性质,即给定当前时刻的状态,未来时刻的状态与过去时刻的状态无关。
-
无记忆性: 布朗运动的增量具有无记忆性质,即在任意时间间隔内的增量与过去的路径无关。
1、定义
数学上,布朗运动可以定义为满足以下条件的随机过程:
- 在任意时间点 t,布朗运动的取值B(t) 是一个随机变量,其期望为0,即 E[B(t)]=0。
- 增量B(t)−B(s) 在时间间隔 [s,t] 上是平稳的,即其均值为0,方差正比于时间间隔的长度 t−s,即 Var[B(t)−B(s)]=t−s。
- 增量B(t)−B(s) 在不重叠的时间间隔上是相互独立的,即对于任意时间点 t1<t2<...<tn,增量 B(ti)−B(ti−1) 是相互独立的随机变量。

2、概率分布及数学特征
维纳过程(布朗运动)的概率分布不是常规的概率分布,因为它在任意时刻的取值是随机的,且其路径是连续但不可导的。然而,我们可以描述维纳过程的一些数学特征。
对于维纳过程 B(t),其数学特征如下:
-
均值: 任意时间点 t 的维纳过程的均值是0,即E[B(t)]=0。
-
方差: 维纳过程在时间间隔 [0,t] 上的方差是 Var[B(t)]=t。
-
协方差: 维纳过程的增量 B(t)−B(s) 在时间间隔 [s,t] 上的协方差是Cov[B(t)−B(s)]=t−s。
-
无界性: 维纳过程的路径是无界的,即在任何时间段内,它的取值可以趋近于正无穷或负无穷。
-
连续性: 维纳过程在任何时间点都是连续的,但路径不可导。
-
马尔可夫性: 维纳过程具有马尔可夫性,即给定当前时刻的状态,未来时刻的状态与过去时刻的状态无关。
-
无记忆性: 维纳过程的增量具有无记忆性质,即在任意时间间隔内的增量与过去的路径无关。


3、性质
性质1:维纳过程是平稳独立增量过程。
性质2:维纳过程是正态过程。
性质3:维纳过程是马尔可夫过程。
性质4:维纳过程是均方连续、均方不可导、均方可积的二阶矩过程
性质5:维纳过程是非平稳过程,但为:平稳增量过程。
四、泊松过程
泊松过程(Poisson process)是一种描述随机事件在连续时间上发生的随机过程。这个过程得名于法国数学家西蒙·德封赛·泊松(Siméon Denis Poisson),他在19世纪初首次引入了这个概念。
泊松过程的主要特征是在任意时间点上发生事件的次数是随机的,并且事件之间的时间间隔是独立且指数分布的。泊松过程通常用于建模稀有事件的随机出现,如电话呼叫、到达服务中心的顾客、放射性粒子的衰变等。
泊松过程的基本定义包括以下几个要素:
-
事件发生次数: 记作 N(t),表示在时间段 [0,t] 内事件发生的次数。
-
独立增量: 对于任意不相交的时间段[s,t],事件发生的次数 N(t)−N(s) 与时间段长度 t−s 是相互独立的。
-
固定平均发生率: 泊松过程具有常数发生率λ,表示单位时间内事件发生的平均次数。即 E[N(t)]=λt,其中 �E 表示期望值。
-
稳定增量: 对于任意时间间隔[t1,t2],事件发生的次数N(t2)−N(t1) 的分布是泊松分布,其均值和方差都等于 λ(t2−t1)。
泊松过程的概率质量函数(PMF)可以表示为:
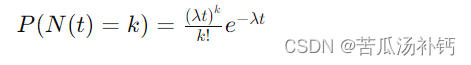
其中,k 表示在时间段[0,t] 内事件发生的次数。
1、定义


定理1:定义1与定义2是等价的。
2、概率分布及数字特征

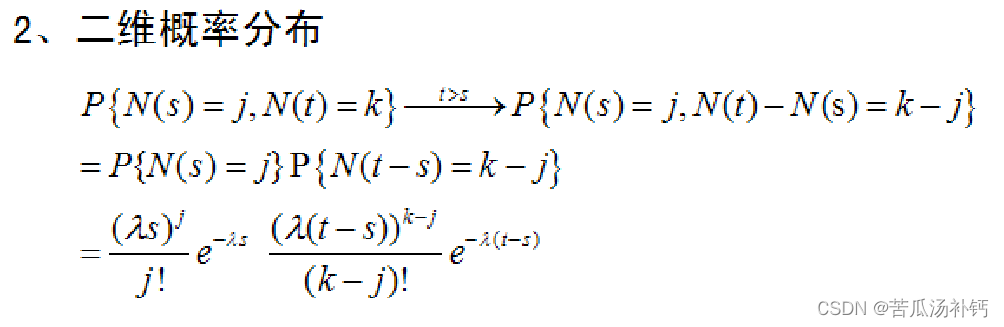

3、性质
性质1:泊松过程是平稳独立增量过程。
性质2:泊松过程是马尔可夫过程。
性质3:泊松过程是生灭过程。
性质4:泊松过程是均方连续、均方不可导、均方可积的二阶矩过程。
性质5:泊松过程是非平稳过程,但为:平稳增量过程。


4、更新计数过程
齐次泊松过程是有相互独立同指数分布的点间间距的计数过程,如果只要求点间间距T,T2,…相互独立同分布,由此可得泊松过程的一个自然推广—更新计数过程。

五、非齐次泊松过程

六、复合泊松过程

总结
-
布朗运动(维纳过程):
- 应用领域: 金融学、物理学、生物学。
- 特点: 连续时间的随机过程,路径连续但不可导,具有马尔可夫性和独立增量性。
-
泊松过程:
- 应用领域: 通信网络、排队论、生物学、金融学。
- 特点: 描述随机事件的发生和计数,具有常数发生率、独立增量和稳定增量的特性。
-
高斯过程:
- 应用领域: 机器学习、回归分析、空间统计学。
- 特点: 具有正态分布的随机过程,可以用均值函数和协方差函数完全描述。常用于建模随机函数